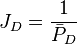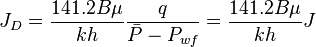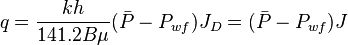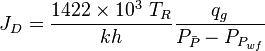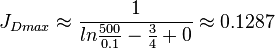Difference between revisions of "JD"
From wiki.pengtools.com
(→Math & Physics) |
(→See Also) |
||
| (69 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
==Brief== | ==Brief== | ||
| − | [[JD]] - dimensionless productivity index, inverse of dimensionless pressure (based on average pressure) <ref name = | + | [[JD]] - dimensionless productivity index<ref name = pushing/>, inverse of dimensionless pressure (based on average pressure) which contains the type of flow regime, boundary condition, drainage shape and stimulation <ref name = DW/>. |
==Math & Physics== | ==Math & Physics== | ||
| − | + | :<math> {J_D} = \frac{1}{\bar{P}_D} </math> | |
| − | |||
| − | :<math> {J_D} = \frac{1}{ | ||
| − | + | From the [[Darcy's law]] for the unfractured well the [[JD]] is: | |
| − | : | ||
| − | Gas | + | <table width="100%" border="1" cellpadding="3" cellspacing="1"> |
| + | <tr> | ||
| + | <th></th> | ||
| + | <th>Well in circular drainage area</th> | ||
| + | <th>Well in a drainage area with the shape factor <math> {C_A}</math><ref name = DW/></th> | ||
| + | |||
| + | </tr> | ||
| + | |||
| + | <tr> | ||
| + | <td>Steady state</td> | ||
| + | <td><math> {J_D} = \frac{1}{ln{\frac{r_e}{r_w}-\frac{1}{2}+S}} </math></td> | ||
| + | <td><math>{J_D} = \frac{1}{\frac{1}{2}ln{\frac{4.5A}{C_A{r_w}^2}+S}}</math></td> | ||
| + | |||
| + | </tr> | ||
| + | |||
| + | <tr> | ||
| + | <td>Pseudo steady state</td> | ||
| + | <td><math> {J_D} = \frac{1}{ln{\frac{r_e}{r_w}-\frac{3}{4}+S}} </math></td> | ||
| + | <td><math>{J_D} = \frac{1}{\frac{1}{2}ln{\frac{2.25A}{C_A{r_w}^2}+S}}</math></td> | ||
| + | </tr> | ||
| + | |||
| + | </table> | ||
| + | |||
| + | |||
| + | Some typical <math> {C_A}</math> values: circle 31.6, square 30.88 <ref name = Dietz/>. | ||
| + | |||
| + | ===Oil=== | ||
| + | :<math> {J_D} = \frac{141.2 B \mu}{kh} \frac{q}{\bar{P} - P_{wf}} = \frac{141.2 B \mu}{kh} J</math> | ||
| + | |||
| + | :<math> {q} = \frac{kh}{141.2 B \mu} (\bar{P} - P_{wf}) J_D = (\bar{P} - P_{wf}) J</math> | ||
| + | |||
| + | ===Gas=== | ||
:<math>J_D=\frac{1422 \times 10^3\ T_R}{kh} \frac{q_g}{P_{\bar{P}}-P_{P_{wf}}}</math> | :<math>J_D=\frac{1422 \times 10^3\ T_R}{kh} \frac{q_g}{P_{\bar{P}}-P_{P_{wf}}}</math> | ||
| + | |||
| + | ==Maximum <math>J_D</math>== | ||
| + | |||
| + | The undamaged unstimulated vertical well potential in a pseudo steady radial flow in a circular drainage area: | ||
| + | |||
| + | :<math> {J_D}_{max} \approx \frac{1}{ln{\frac{500}{0.1}-\frac{3}{4}+0}} \approx 0.1287</math> | ||
| + | |||
| + | The maximum possible stimulated well potential for pseudo steady linear flow is: | ||
| + | |||
| + | <math>{J_D}_{max}= \frac{6}{\pi} \approx 1.91 </math> , see [[6/π stimulated well potential]] | ||
| + | |||
| + | The maximum possible stimulated well potential for steady state linear flow is: | ||
| + | |||
| + | <math>{J_D}_{max}= \frac{4}{\pi} \approx 1.27 </math> , see [[4/π stimulated well potential]] | ||
| + | |||
| + | == Nomenclature == | ||
| + | :<math> B </math> = formation volume factor, bbl/stb | ||
| + | :<math> C_A </math> = Dietz shape factor, dimensionless | ||
| + | :<math> J </math> = productivity index, stb/psia | ||
| + | :<math> J_D </math> = dimensionless productivity index, dimensionless | ||
| + | :<math> kh</math> = permeability times thickness, md*ft | ||
| + | :<math> \bar{P} </math> = average reservoir pressure, psia | ||
| + | :<math> \bar{P}_D</math> = dimensionless pressure (based on average pressure), dimensionless | ||
| + | :<math> P_{\bar{P}} </math> = average reservoir pseudopressure, psia<sup>2</sup>/cP | ||
| + | :<math> P_{wf} </math> = well flowing pressure, psia | ||
| + | :<math> P_{P_{wf}} </math> = average well flowing pseudopressure, psia<sup>2</sup>/cP | ||
| + | :<math> q </math> = flowing rate, stb/d | ||
| + | :<math> q_g </math> = gas rate, MMscfd | ||
| + | :<math> r_w </math> = wellbore radius, ft | ||
| + | :<math> r_e </math> = drainage radius, ft | ||
| + | :<math> S </math> = skin factor, dimensionless | ||
| + | :<math> T </math> = temperature, °R | ||
| + | |||
| + | ===Greek symbols=== | ||
| + | |||
| + | :<math> \mu </math> = viscosity, cp | ||
| + | |||
| + | ==See Also== | ||
| + | |||
| + | * [[Darcy's law]] | ||
| + | * [[IPR]] | ||
| + | * [[Productivity index|J]] | ||
| + | * [[Production Potential]] | ||
== References == | == References == | ||
| Line 27: | Line 98: | ||
|url=https://www.onepetro.org/conference-paper/SPE-91760-MS | |url=https://www.onepetro.org/conference-paper/SPE-91760-MS | ||
|url-access=registration | |url-access=registration | ||
| + | }}</ref> | ||
| + | <ref name=DW> | ||
| + | {{cite book | ||
| + | |last1= Wolcott |first1=Don | ||
| + | |title=Applied Waterflood Field Development | ||
| + | |date=2009 | ||
| + | |publisher=Energy Tribune Publishing Inc | ||
| + | |place=Houston | ||
| + | |url=https://www.amazon.com/Applied-Waterflood-Field-Development-Wolcott/dp/0578023946/ref=sr_1_1?ie=UTF8&qid=1481788841&sr=8-1&keywords=Don+wolcott | ||
| + | |url-access=subscription | ||
}}</ref> | }}</ref> | ||
| + | <ref name= Dietz >{{cite journal | ||
| + | |last1=Dietz|first1=D.N. | ||
| + | |title=Determination of Average Reservoir Pressure From Build-Up Surveys | ||
| + | |publisher=J Pet Technol | ||
| + | |number=SPE-1156-PA | ||
| + | |date=1965 | ||
| + | |url=https://doi.org/10.2118/1156-PA | ||
| + | |url-access=registration | ||
| + | }}</ref> | ||
</references> | </references> | ||
| + | [[Category:optiFrac]] | ||
| + | [[Category:optiFracMS]] | ||
| + | [[Category:fracDesign]] | ||
[[Category:pengtools]] | [[Category:pengtools]] | ||
[[Category:E&P Portal]] | [[Category:E&P Portal]] | ||
| + | |||
| + | {{#seo: | ||
| + | |title=Dimensionless Productivity Index | ||
| + | |titlemode= replace | ||
| + | |keywords=hydraulic fracturing, hydraulic fracturing formulas, well potential, productivity index | ||
| + | |description=JD dimensionless productivity index | ||
| + | }} | ||
| + | <div style='text-align: right;'>By Mikhail Tuzovskiy on {{REVISIONTIMESTAMP}}</div> | ||
Latest revision as of 14:53, 7 April 2025
Contents
Brief
JD - dimensionless productivity index[1], inverse of dimensionless pressure (based on average pressure) which contains the type of flow regime, boundary condition, drainage shape and stimulation [2].
Math & Physics
From the Darcy's law for the unfractured well the JD is:
| Well in circular drainage area | Well in a drainage area with the shape factor 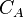 [2] [2] |
|
|---|---|---|
| Steady state | 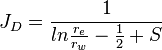 |
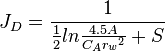 |
| Pseudo steady state | 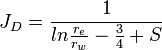 |
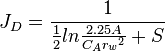 |
Some typical 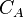 values: circle 31.6, square 30.88 [3].
values: circle 31.6, square 30.88 [3].
Oil
Gas
Maximum 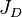
The undamaged unstimulated vertical well potential in a pseudo steady radial flow in a circular drainage area:
The maximum possible stimulated well potential for pseudo steady linear flow is:
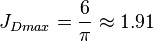 , see 6/π stimulated well potential
, see 6/π stimulated well potential
The maximum possible stimulated well potential for steady state linear flow is:
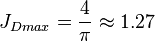 , see 4/π stimulated well potential
, see 4/π stimulated well potential
Nomenclature
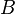 = formation volume factor, bbl/stb
= formation volume factor, bbl/stb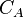 = Dietz shape factor, dimensionless
= Dietz shape factor, dimensionless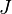 = productivity index, stb/psia
= productivity index, stb/psia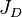 = dimensionless productivity index, dimensionless
= dimensionless productivity index, dimensionless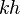 = permeability times thickness, md*ft
= permeability times thickness, md*ft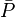 = average reservoir pressure, psia
= average reservoir pressure, psia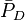 = dimensionless pressure (based on average pressure), dimensionless
= dimensionless pressure (based on average pressure), dimensionless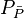 = average reservoir pseudopressure, psia2/cP
= average reservoir pseudopressure, psia2/cP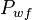 = well flowing pressure, psia
= well flowing pressure, psia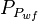 = average well flowing pseudopressure, psia2/cP
= average well flowing pseudopressure, psia2/cP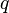 = flowing rate, stb/d
= flowing rate, stb/d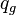 = gas rate, MMscfd
= gas rate, MMscfd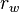 = wellbore radius, ft
= wellbore radius, ft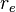 = drainage radius, ft
= drainage radius, ft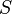 = skin factor, dimensionless
= skin factor, dimensionless = temperature, °R
= temperature, °R
Greek symbols
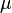 = viscosity, cp
= viscosity, cp
See Also
References
- ↑ Rueda, J.I.; Mach, J.; Wolcott, D. (2004). "Pushing Fracturing Limits to Maximize Producibility in Turbidite Formations in Russia"
 (SPE-91760-MS). Society of Petroleum Engineers.
(SPE-91760-MS). Society of Petroleum Engineers.
- ↑ 2.0 2.1
Wolcott, Don (2009). Applied Waterflood Field Development
 . Houston: Energy Tribune Publishing Inc.
. Houston: Energy Tribune Publishing Inc.
- ↑ Dietz, D.N. (1965). "Determination of Average Reservoir Pressure From Build-Up Surveys"
 (SPE-1156-PA). J Pet Technol.
(SPE-1156-PA). J Pet Technol.
By Mikhail Tuzovskiy on 20250407145307