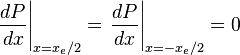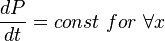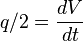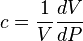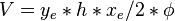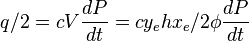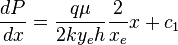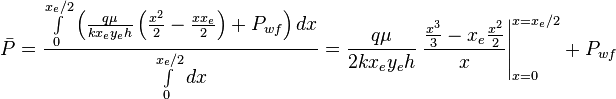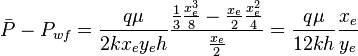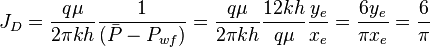6/π stimulated well potential
From wiki.pengtools.com
Brief
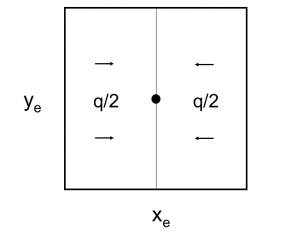
6/π is the maximum possible stimulation well potential for pseudo steady state linear flow in a square well spacing.
Math & Physics
Pseudo steady state flow boundary conditions:
From Diffusivity Equation:
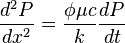 ( 1 )
( 1 )
From Material Balance:
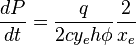 ( 2 )
( 2 )
( 2 ) - > ( 1 ) :
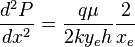 ( 3 )
( 3 )
Integrating ( 3 ):
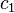 must satisfy boundary condition:
must satisfy boundary condition: 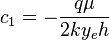
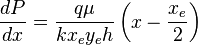 ( 4 )
( 4 )
Integrating ( 4 ):
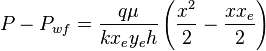 ( 5 )
( 5 )
Since average pressure is: 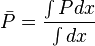 :
:
See also
4/π stimulated well potential
JD
optiFrac
fracDesign
Production Potential
Nomenclature
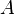 = cross-sectional area, cm2
= cross-sectional area, cm2 = total compressibility, atm-1
= total compressibility, atm-1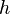 = thickness, m
= thickness, m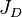 = dimensionless productivity index, dimensionless
= dimensionless productivity index, dimensionless = permeability, d
= permeability, d = pressure, atm
= pressure, atm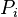 = initial pressure, atm
= initial pressure, atm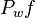 = well flowing pressure, atm
= well flowing pressure, atm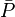 = average pressure, atm
= average pressure, atm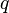 = flow rate, cm3/sec
= flow rate, cm3/sec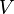 = one wing volume, m3
= one wing volume, m3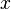 = length, m
= length, m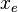 = drinage area length, m
= drinage area length, m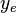 = drinage area width, m
= drinage area width, m
Greek symbols
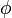 = porosity, fraction
= porosity, fraction 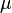 =viscosity, cp
=viscosity, cp