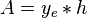Diffusivity Equation
From wiki.pengtools.com
Diffusivity Equation Derivation
From Mass conservation:
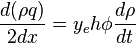 ( 1 )
( 1 )
From Darcy's law:
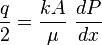 ( 2 )
( 2 )
( 2 ) →( 1 ):
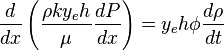 ( 3 )
( 3 )
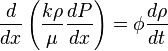 ( 4 )
( 4 )
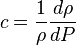 ( 5 )
( 5 )
( 5 ) -> ( 4 ):
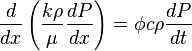 ( 6 )
( 6 )
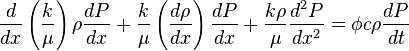 ( 7 )
( 7 )
Assumption that viscosity is constant cancels out first term in left hand side of (7):
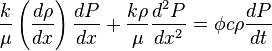 ( 8 )
( 8 )
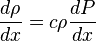 ( 9 )
( 9 )
( 9 ) -> ( 8 ):
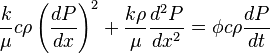 ( 10 )
( 10 )
Term 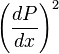 in (10) is second order of magnitude low and can be cancelled out, which yields:
in (10) is second order of magnitude low and can be cancelled out, which yields:
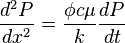 ( 11 )
( 11 )