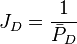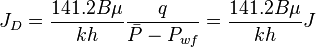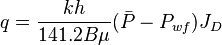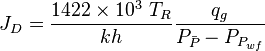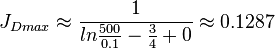JD
From wiki.pengtools.com
Contents
Brief
JD - dimensionless productivity index[1], inverse of dimensionless pressure (based on average pressure) which contains the type of flow regime, boundary condition, drainage shape and stimulation [2].
Math & Physics
From the Darcy's law for the unfractured well the JD is:
| Well in circular drainage area | Well in a drainage area with the shape factor 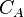 [2] [2] |
|
|---|---|---|
| Steady state | 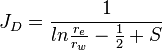 |
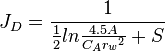 |
| Pseudo steady state | 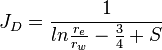 |
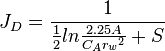 |
Some typical 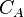 values: circle 31.6, square 30.88 [3].
values: circle 31.6, square 30.88 [3].
Oil
Gas
Maximum 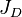
The undamaged unstimulated vertical well potential in a pseudo steady radial flow in a circular drainage area:
The maximum possible stimulated well potential for pseudo steady linear flow is:
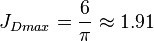 , see 6/π stimulated well potential
, see 6/π stimulated well potential
The maximum possible stimulated well potential for steady state linear flow is:
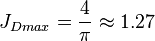 , see 4/π stimulated well potential
, see 4/π stimulated well potential
Nomenclature
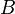 = formation volume factor, bbl/stb
= formation volume factor, bbl/stb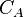 = Dietz shape factor, dimensionless
= Dietz shape factor, dimensionless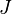 = productivity index, stb/psia
= productivity index, stb/psia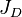 = dimensionless productivity index, dimensionless
= dimensionless productivity index, dimensionless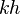 = permeability times thickness, md*ft
= permeability times thickness, md*ft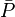 = average reservoir pressure, psia
= average reservoir pressure, psia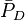 = dimensionless pressure (based on average pressure), dimensionless
= dimensionless pressure (based on average pressure), dimensionless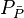 = average reservoir pseudopressure, psia2/cP
= average reservoir pseudopressure, psia2/cP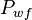 = well flowing pressure, psia
= well flowing pressure, psia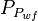 = average well flowing pseudopressure, psia2/cP
= average well flowing pseudopressure, psia2/cP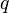 = flowing rate, stb/d
= flowing rate, stb/d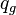 = gas rate, MMscfd
= gas rate, MMscfd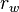 = wellbore radius, ft
= wellbore radius, ft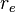 = drainage radius, ft
= drainage radius, ft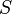 = skin factor, dimensionless
= skin factor, dimensionless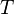 = temperature, °R
= temperature, °R
Greek symbols
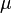 = viscosity, cp
= viscosity, cp
See Also
References
- ↑ Rueda, J.I.; Mach, J.; Wolcott, D. (2004). "Pushing Fracturing Limits to Maximize Producibility in Turbidite Formations in Russia"
 (SPE-91760-MS). Society of Petroleum Engineers.
(SPE-91760-MS). Society of Petroleum Engineers.
- ↑ 2.0 2.1
Wolcott, Don (2009). Applied Waterflood Field Development
 . Houston: Energy Tribune Publishing Inc.
. Houston: Energy Tribune Publishing Inc.
- ↑ Dietz, D.N. (1965). "Determination of Average Reservoir Pressure From Build-Up Surveys"
 (SPE-1156-PA). J Pet Technol.
(SPE-1156-PA). J Pet Technol.
By Mikhail Tuzovskiy on 20230712123204