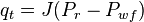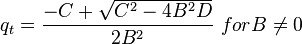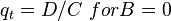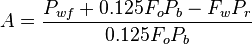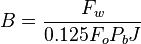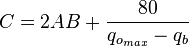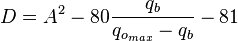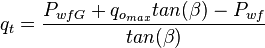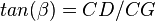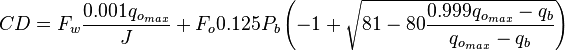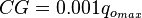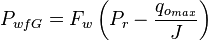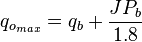3 Phase IPR

Three-phase Inflow Performance Relationship

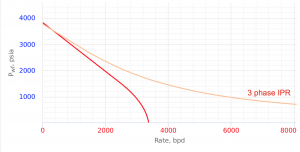
3 Phase IPR Curve

3 Phase IPR calculates IPR curve for oil wells producing water.

3 Phase IPR equation was derived by Petrobras based on combination of Vogel's IPR equation for oil flow and constant productivity for water flow .

3 Phase IPR curve is determined geometrically from those equations considering the fractional flow of oil and water .

Math and Physics

Total flow rate equations:

For P_b < P_wf < P_r

For pressures between reservoir pressure and bubble point pressure:

$q_t =J (P_r - P_{wf})$

For P_wfG < P_wf < P_b

For pressures between the bubble point pressure and the flowing bottom-hole pressures:

$q_t =\frac{-C+\sqrt{C^2-4B^2D}}{2B^2}\ for B \ne 0$

$q_t =D/C\ for B = 0$

where:

$A=\frac{P_{wf}+0.125F_oP_b-F_wP_r}{0.125F_oP_b}$

$B=\frac{F_w}{0.125F_oP_bJ}$

$C=2AB+\frac{80}{q_{o_{max}}-q_b}$

$D=A^2-80\frac{q_b}{q_{o_{max}}-q_b}-81$

For 0 < P_wf < P_wfG

$q_t =\frac{P_{wfG}+q_{o_{max}}tan(\beta)-P_{wf}}{tan(\beta)}$

where:

$tan(\beta) = CD/CG$

$CD = F_w\frac{0.001q_{o_{max}}}{J}+F_o0.125P_b \left ( -1+\sqrt{81-80 \frac{0.999q_{o_{max}}-q_b}{q_{o_{max}}-q_b}} \right)$

$CG = 0.001 q_{o_{max}}$

And

$P_{wfG}=F_w \left ( P_r - \frac{q_{o_{max}}}{J}\right )$

$q_{o_{max}}=q_b+\frac{JP_b}{1.8}$

IPR calculator software

• PQplot nodal analysis software is used to calculate the IPR curves. PQplot is available online at www.pengtools.com.
• Excel
• other

Nomenclature

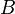$B$ = formation volume factor, bbl/stb

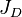$J_D$ = dimensionless productivity index, dimensionless

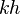$kh$ = permeability times thickness, md*ft

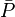$\bar{P}$ = average reservoir pressure, psia

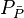$P_{\bar{P}}$ = average reservoir pseudopressure, psia²/cP

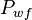$P_{wf}$ = well flowing pressure, psia

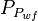$P_{P_{wf}}$ = average well flowing pseudopressure, psia²/cP

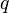$q$ = flowing rate, stb/d

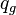$q_g$ = gas rate, MMscfd

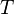$T$ = temperature, °R

Greek symbols

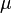$\mu$ = viscosity, cp

See also

141.2 derivation

Darcy's law

JD

Production Potential