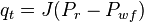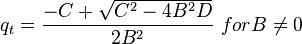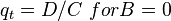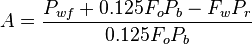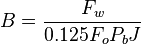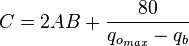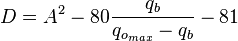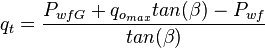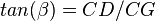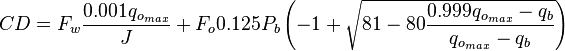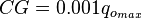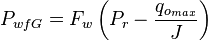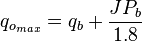Difference between revisions of "3 Phase IPR"

From wiki.pengtools.com
Jump to: navigation, search
(→‎For 0 wf wfG)
Line 14: Line 14:
 
===For P<sub>b</sub> < P<sub>wf</sub> < P<sub>r</sub>===
 
===For P<sub>b</sub> < P<sub>wf</sub> < P<sub>r</sub>===
 
For pressures between reservoir pressure and bubble point pressure:
 
For pressures between reservoir pressure and bubble point pressure:
−
:<math> q_t =J (P_r - P_{wf})</math>  
+
:<math> q_t =J (P_r - P_{wf})</math> <ref name=KermitBrown1984/>
  
 
===For P<sub>wfG</sub> < P<sub>wf</sub> < P<sub>b</sub>===
 
===For P<sub>wfG</sub> < P<sub>wf</sub> < P<sub>b</sub>===
 
For pressures between the bubble point pressure and the flowing bottom-hole pressures:
 
For pressures between the bubble point pressure and the flowing bottom-hole pressures:
−
:<math> q_t =\frac{-C+\sqrt{C^2-4B^2D}}{2B^2}\ for B \ne 0</math>
+
:<math> q_t =\frac{-C+\sqrt{C^2-4B^2D}}{2B^2}\ for B \ne 0</math><ref name=KermitBrown1984/>
−
:<math> q_t =D/C\ for B = 0</math>
+
:<math> q_t =D/C\ for B = 0</math><ref name=KermitBrown1984/>
  
 
where:
 
where:
  
−
:<math> A=\frac{P_{wf}+0.125F_oP_b-F_wP_r}{0.125F_oP_b}</math>
+
:<math> A=\frac{P_{wf}+0.125F_oP_b-F_wP_r}{0.125F_oP_b}</math><ref name=KermitBrown1984/>
−
:<math> B=\frac{F_w}{0.125F_oP_bJ}</math>
+
:<math> B=\frac{F_w}{0.125F_oP_bJ}</math><ref name=KermitBrown1984/>
−
:<math> C=2AB+\frac{80}{q_{o_{max}}-q_b}</math>
+
:<math> C=2AB+\frac{80}{q_{o_{max}}-q_b}</math><ref name=KermitBrown1984/>
−
:<math> D=A^2-80\frac{q_b}{q_{o_{max}}-q_b}-81</math>
+
:<math> D=A^2-80\frac{q_b}{q_{o_{max}}-q_b}-81</math><ref name=KermitBrown1984/>
  
 
=== For 0 < P<sub>wf</sub> < P<sub>wfG</sub>===
 
=== For 0 < P<sub>wf</sub> < P<sub>wfG</sub>===
−
:<math> q_t =\frac{P_{wfG}+q_{o_{max}}tan(\beta)-P_{wf}}{tan(\beta)}</math>
+
:<math> q_t =\frac{P_{wfG}+q_{o_{max}}tan(\beta)-P_{wf}}{tan(\beta)}</math><ref name=KermitBrown1984/>
  
 
where:
 
where:
  
−
:<math> tan(\beta) = CD/CG </math>
+
:<math> tan(\beta) = CD/CG </math><ref name=KermitBrown1984/>
−
:<math> CD = F_w\frac{0.001q_{o_{max}}}{J}+F_o0.125P_b \left ( -1+\sqrt{81-80 \frac{0.999q_{o_{max}}-q_b}{q_{o_{max}}-q_b}} \right)</math>
+
:<math> CD = F_w\frac{0.001q_{o_{max}}}{J}+F_o0.125P_b \left ( -1+\sqrt{81-80 \frac{0.999q_{o_{max}}-q_b}{q_{o_{max}}-q_b}} \right)</math><ref name=KermitBrown1984/>
−
:<math> CG = 0.001 q_{o_{max}}</math>
+
:<math> CG = 0.001 q_{o_{max}}</math><ref name=KermitBrown1984/>
  
 
===And===
 
===And===
−
:<math> P_{wfG}=F_w \left ( P_r - \frac{q_{o_{max}}}{J}\right )</math>
+
:<math> P_{wfG}=F_w \left ( P_r - \frac{q_{o_{max}}}{J}\right )</math><ref name=KermitBrown1984/>
−
:<math> q_{o_{max}}=q_b+\frac{JP_b}{1.8}</math>
+
:<math> q_{o_{max}}=q_b+\frac{JP_b}{1.8}</math><ref name=KermitBrown1984/>
  
 
==IPR calculator software==
 
==IPR calculator software==

Revision as of 08:44, 11 April 2019

Three-phase Inflow Performance Relationship

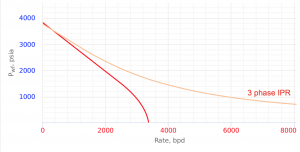
3 Phase IPR Curve [1]

3 Phase IPR calculates IPR curve for oil wells producing water.

3 Phase IPR equation was derived by Petrobras based on combination of Vogel's IPR equation for oil flow and constant productivity for water flow [1].

3 Phase IPR curve is determined geometrically from those equations considering the fractional flow of oil and water [1].

Math and Physics

Total flow rate equations:

For Pb < Pwf < Pr

For pressures between reservoir pressure and bubble point pressure:

q_t =J (P_r - P_{wf}) [1]

For PwfG < Pwf < Pb

For pressures between the bubble point pressure and the flowing bottom-hole pressures:

q_t =\frac{-C+\sqrt{C^2-4B^2D}}{2B^2}\ for B \ne 0[1]
q_t =D/C\ for B = 0[1]

where:

A=\frac{P_{wf}+0.125F_oP_b-F_wP_r}{0.125F_oP_b}[1]
B=\frac{F_w}{0.125F_oP_bJ}[1]
C=2AB+\frac{80}{q_{o_{max}}-q_b}[1]
D=A^2-80\frac{q_b}{q_{o_{max}}-q_b}-81[1]

For 0 < Pwf < PwfG

q_t =\frac{P_{wfG}+q_{o_{max}}tan(\beta)-P_{wf}}{tan(\beta)}[1]

where:

tan(\beta) = CD/CG [1]
CD = F_w\frac{0.001q_{o_{max}}}{J}+F_o0.125P_b \left ( -1+\sqrt{81-80 \frac{0.999q_{o_{max}}-q_b}{q_{o_{max}}-q_b}} \right)[1]
CG = 0.001 q_{o_{max}}[1]

And

P_{wfG}=F_w \left ( P_r - \frac{q_{o_{max}}}{J}\right )[1]
q_{o_{max}}=q_b+\frac{JP_b}{1.8}[1]

IPR calculator software

Nomenclature

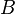B = formation volume factor, bbl/stb
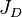J_D = dimensionless productivity index, dimensionless
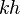kh = permeability times thickness, md*ft
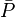\bar{P} = average reservoir pressure, psia
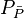P_{\bar{P}} = average reservoir pseudopressure, psia2/cP
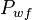P_{wf} = well flowing pressure, psia
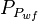P_{P_{wf}} = average well flowing pseudopressure, psia2/cP
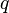q = flowing rate, stb/d
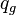q_g = gas rate, MMscfd
T = temperature, °R

Greek symbols

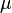\mu = viscosity, cp

References

  1. ↑ Jump up to: 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 1.12 1.13 1.14 1.15 Brown, Kermit (1984). The Technology of Artificial Lift Methods. Volume 4. Production Optimization of Oil and Gas Wells by Nodal System Analysis. Tulsa, Oklahoma: PennWellBookss. 

See also

141.2 derivation
Darcy's law
JD
Production Potential
Retrieved from "https://wiki.pengtools.com/index.php?title=3_Phase_IPR&oldid=6079"