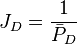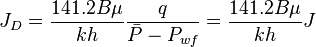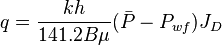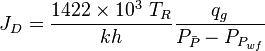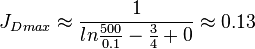Difference between revisions of "JD"

Revision as of 11:29, 11 July 2023

Brief

JD - dimensionless productivity index^[1], inverse of dimensionless pressure (based on average pressure) which contains the type of flow regime, boundary condition, drainage shape and stimulation ^[2].

Math & Physics

{J_D} = \frac{1}{\bar{P}_D}

From the Darcy's law for an unfractured well located in the center of a circular drainage area, the JD is:

Pseudo-steady state:

{J_D} = \frac{1}{ln{\frac{r_e}{r_w}-\frac{3}{4}+S}}

Steady state:

{J_D} = \frac{1}{ln{\frac{r_e}{r_w}-\frac{1}{2}+S}}

${J_D}$	Well in circular drainage area	Well in the drainage area with the shape factor 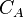${C_A}$
Steady state	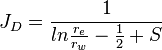${J_D} = \frac{1}{ln{\frac{r_e}{r_w}-\frac{1}{2}+S}}$	Calculated with Nodal Analysis using the PQplot by setting the flowing wellhead pressure (FWHP) equal to the current flowing line pressure (FLP) at the well head. Use the current value of JD.
Pseudo steady state	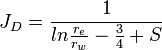${J_D} = \frac{1}{ln{\frac{r_e}{r_w}-\frac{3}{4}+S}}$	Calculated the same way as for the Gas Flowing case

Oil

{J_D} = \frac{141.2 B \mu}{kh} \frac{q}{\bar{P} - P_{wf}} = \frac{141.2 B \mu}{kh} J

{q} = \frac{kh}{141.2 B \mu} (\bar{P} - P_{wf}) J_D

Gas

J_D=\frac{1422 \times 10^3\ T_R}{kh} \frac{q_g}{P_{\bar{P}}-P_{P_{wf}}}

Maximum $J_D$

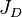
The undamaged unstimulated vertical well potential in a pseudo steady radial flow is:

{J_D}_{max} \approx \frac{1}{ln{\frac{500}{0.1}-\frac{3}{4}+0}} \approx 0.13

The maximum possible stimulated well potential for pseudo steady linear flow is:

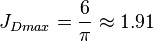${J_D}_{max}= \frac{6}{\pi} \approx 1.91$ , see 6/π stimulated well potential

The maximum possible stimulated well potential for steady state linear flow is:

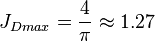${J_D}_{max}= \frac{4}{\pi} \approx 1.27$ , see 4/π stimulated well potential

Nomenclature

B

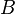= formation volume factor, bbl/stb

J

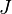= productivity index, stb/psia

J_D

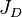= dimensionless productivity index, dimensionless

kh

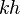= permeability times thickness, md*ft

\bar{P}

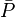= average reservoir pressure, psia

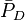\bar{P}_D

= dimensionless pressure (based on average pressure), dimensionless

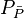P_{\bar{P}}

= average reservoir pseudopressure, psia²/cP

P_{wf}

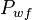= well flowing pressure, psia

P_{P_{wf}}

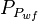= average well flowing pseudopressure, psia²/cP

q

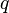= flowing rate, stb/d

q_g

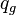= gas rate, MMscfd

r_w

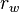= wellbore radius, ft

r_e

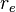= drainage radius, ft

S

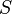= skin factor, dimensionless

T

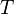= temperature, °R

Greek symbols

\mu

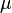= viscosity, cp

References

↑ Rueda, J.I.; Mach, J.; Wolcott, D. (2004). "Pushing Fracturing Limits to Maximize Producibility in Turbidite Formations in Russia" (SPE-91760-MS). Society of Petroleum Engineers.
↑ Cite error: Invalid <ref> tag; no text was provided for refs named DW

[pushing-1] Rueda, J.I.; Mach, J.; Wolcott, D. (2004). "Pushing Fracturing Limits to Maximize Producibility in Turbidite Formations in Russia" (SPE-91760-MS). Society of Petroleum Engineers.

[DW-2] Cite error: Invalid <ref> tag; no text was provided for refs named DW

[1]

[2]

@@ Line 21: / Line 21: @@
 <th>Well in circular drainage area</th>
 <th>Well in the drainage area with the shape factor <math> {C_A} </math></th>
-<th>Workover Potential (WOP)</th>
 </tr>
 <tr>
-<td>Gas</td>
+<td>Steady state</td>
-<td>Flowing</td>
+<td><math> {J_D} = \frac{1}{ln{\frac{r_e}{r_w}-\frac{1}{2}+S}} </math></td>
 <td> Calculated with Nodal Analysis using the [[PQplot]] by setting the flowing wellhead pressure (FWHP) equal to the current flowing line pressure (FLP) at the well head. <BR>Use the current value of [[JD]].</td>
-<td> Calculated with Nodal Analysis using the [[PQplot]] by using the largest tubing practical that will fit in the current well bore with a FWHP equal to the current FLP. The largest tubing size is approximately the casing drift diameter minus the tubing coupling diameter > 0.5 inches for clearance (see [[Pipe Catalog]]).<BR>Use [[JD]]=0.13.</td>
 </tr>
 <tr>
-<td>Oil</td>
+<td>Pseudo steady state</td>
-<td>Flowing</td>
+<td><math> {J_D} = \frac{1}{ln{\frac{r_e}{r_w}-\frac{3}{4}+S}} </math></td>
 <td>Calculated the same way as for the '''Gas Flowing''' case</td>
-<td>Calculated as absolute open flow (AOF).<BR>Use [[JD]]=1.27.</td>
-</tr>
-<tr>
-<td>Oil</td>
-<td>Artificial Lift (ESP, Rod Pump, PCP)</td>
-<td>Calculated by setting the flowing bottomhole pressure (Pwf) equal to the fluid level at the pump depth.<BR>Use the current value of [[JD]].</td>
-<td>Calculated as absolute open flow (AOF).<BR>Use [[JD]]=1.27. <BR>Note: If WOP > all lift capacities thats good, must engineer a higher performance system.</td>
 </tr>

Navigation menu

Navigation

Categories

Products