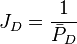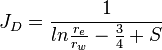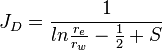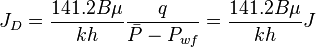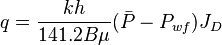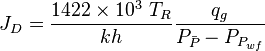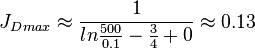Difference between revisions of "JD"

From wiki.pengtools.com
Jump to: navigation, search
(→‎Math & Physics)
Line 15: Line 15:
 
Steady state:
 
Steady state:
 
:<math> {J_D} = \frac{1}{ln{\frac{r_e}{r_w}-\frac{1}{2}+S}} </math>
 
:<math> {J_D} = \frac{1}{ln{\frac{r_e}{r_w}-\frac{1}{2}+S}} </math>
 +
 +
<table width="100%" border="1" cellpadding="3" cellspacing="1">
 +
<tr>
 +
<th><math> {J_D} </math></th>
 +
<th>Well in circular drainage area</th>
 +
<th>Well in the drainage area with the shape factor <math> {C_A} </math></th>
 +
<th>Workover Potential (WOP)</th>
 +
 +
</tr>
 +
 +
<tr>
 +
<td>Gas</td>
 +
<td>Flowing</td>
 +
<td> Calculated with Nodal Analysis using the [[PQplot]] by setting the flowing wellhead pressure (FWHP) equal to the current flowing line pressure (FLP) at the well head. <BR>Use the current value of [[JD]].</td>
 +
<td> Calculated with Nodal Analysis using the [[PQplot]] by using the largest tubing practical that will fit in the current well bore with a FWHP equal to the current FLP. The largest tubing size is approximately the casing drift diameter minus the tubing coupling diameter > 0.5 inches for clearance (see [[Pipe Catalog]]).<BR>Use [[JD]]=0.13.</td>
 +
</tr>
 +
 +
<tr>
 +
<td>Oil</td>
 +
<td>Flowing</td>
 +
<td>Calculated the same way as for the '''Gas Flowing''' case</td>
 +
<td>Calculated as absolute open flow (AOF).<BR>Use [[JD]]=1.27.</td>
 +
</tr>
 +
 +
<tr>
 +
<td>Oil</td>
 +
<td>Artificial Lift (ESP, Rod Pump, PCP)</td>
 +
<td>Calculated by setting the flowing bottomhole pressure (Pwf) equal to the fluid level at the pump depth.<BR>Use the current value of [[JD]].</td>
 +
<td>Calculated as absolute open flow (AOF).<BR>Use [[JD]]=1.27. <BR>Note: If WOP > all lift capacities thats good, must engineer a higher performance system.</td>
 +
</tr>
 +
 +
</table>
  
 
===Oil===
 
===Oil===

Revision as of 11:27, 11 July 2023

Brief

JD - dimensionless productivity index[1], inverse of dimensionless pressure (based on average pressure) which contains the type of flow regime, boundary condition, drainage shape and stimulation [2].

Math & Physics

{J_D} = \frac{1}{\bar{P}_D}

From the Darcy's law for an unfractured well located in the center of a circular drainage area, the JD is:

Pseudo-steady state:

{J_D} = \frac{1}{ln{\frac{r_e}{r_w}-\frac{3}{4}+S}}

Steady state:

{J_D} = \frac{1}{ln{\frac{r_e}{r_w}-\frac{1}{2}+S}}
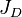{J_D} Well in circular drainage area Well in the drainage area with the shape factor 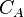{C_A} Workover Potential (WOP)
Gas Flowing Calculated with Nodal Analysis using the PQplot by setting the flowing wellhead pressure (FWHP) equal to the current flowing line pressure (FLP) at the well head.
Use the current value of JD.		 Calculated with Nodal Analysis using the PQplot by using the largest tubing practical that will fit in the current well bore with a FWHP equal to the current FLP. The largest tubing size is approximately the casing drift diameter minus the tubing coupling diameter > 0.5 inches for clearance (see Pipe Catalog).
Use JD=0.13.
Oil Flowing Calculated the same way as for the Gas Flowing case Calculated as absolute open flow (AOF).
Use JD=1.27.
Oil Artificial Lift (ESP, Rod Pump, PCP) Calculated by setting the flowing bottomhole pressure (Pwf) equal to the fluid level at the pump depth.
Use the current value of JD.		 Calculated as absolute open flow (AOF).
Use JD=1.27.
Note: If WOP > all lift capacities thats good, must engineer a higher performance system.

Oil

{J_D} = \frac{141.2 B \mu}{kh} \frac{q}{\bar{P} - P_{wf}} = \frac{141.2 B \mu}{kh} J
{q} = \frac{kh}{141.2 B \mu} (\bar{P} - P_{wf}) J_D

Gas

J_D=\frac{1422 \times 10^3\ T_R}{kh} \frac{q_g}{P_{\bar{P}}-P_{P_{wf}}}

Maximum J_D

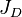
The undamaged unstimulated vertical well potential in a pseudo steady radial flow is:

{J_D}_{max} \approx \frac{1}{ln{\frac{500}{0.1}-\frac{3}{4}+0}} \approx 0.13

The maximum possible stimulated well potential for pseudo steady linear flow is:

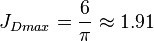{J_D}_{max}= \frac{6}{\pi} \approx 1.91 , see 6/π stimulated well potential

The maximum possible stimulated well potential for steady state linear flow is:

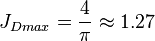{J_D}_{max}= \frac{4}{\pi} \approx 1.27 , see 4/π stimulated well potential

Nomenclature

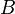B = formation volume factor, bbl/stb
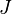J = productivity index, stb/psia
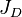J_D = dimensionless productivity index, dimensionless
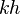kh = permeability times thickness, md*ft
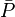\bar{P} = average reservoir pressure, psia
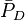\bar{P}_D = dimensionless pressure (based on average pressure), dimensionless
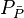P_{\bar{P}} = average reservoir pseudopressure, psia2/cP
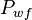P_{wf} = well flowing pressure, psia
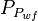P_{P_{wf}} = average well flowing pseudopressure, psia2/cP
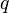q = flowing rate, stb/d
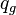q_g = gas rate, MMscfd
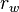r_w = wellbore radius, ft
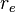r_e = drainage radius, ft
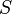S = skin factor, dimensionless
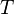T = temperature, °R

Greek symbols

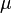\mu = viscosity, cp

See Also

References

  1. ↑ Rueda, J.I.; Mach, J.; Wolcott, D. (2004). "Pushing Fracturing Limits to Maximize Producibility in Turbidite Formations in Russia"Free registration required (SPE-91760-MS). Society of Petroleum Engineers. 
  2. ↑ Cite error: Invalid <ref> tag; no text was provided for refs named DW
Retrieved from "https://wiki.pengtools.com/index.php?title=JD&oldid=7675"