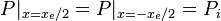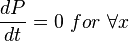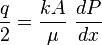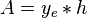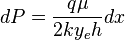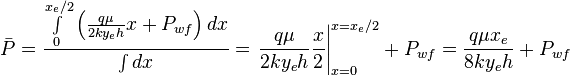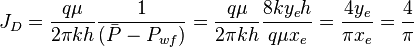Difference between revisions of "4/π stimulated well potential"

From wiki.pengtools.com
Jump to: navigation, search
(→‎Math & Physics)
(→‎Brief)
 
(55 intermediate revisions by the same user not shown)
Line 2: Line 2:
 
[[File:fracture linear flow.png|thumb|right|300px| Stimulated well drainage]]
 
[[File:fracture linear flow.png|thumb|right|300px| Stimulated well drainage]]
  
−
[[4/π stimulated well potential |4/π]] is the maximum possible stimulation potential for steady state linear flow in a square well spacing.
+
[[4/π stimulated well potential |4/π]] is the maximum possible stimulation well potential for steady state linear flow in a square well spacing.
  
 
==Math & Physics==
 
==Math & Physics==
Line 8: Line 8:
 
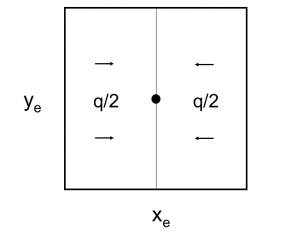
Steady state flow boundary conditions:
 
Steady state flow boundary conditions:
  
−
<math>P |_{x=x_e/2} = P |_{x=-x_e/2} = P_i</math>
+
:<math>P |_{x=x_e/2} = P |_{x=-x_e/2} = P_i</math>
  
−
<math> \frac{dp}{dt} =0\ for \ \forall x </math>
+
:<math> \frac{dP}{dt} =0\ for \ \forall x </math>
  
 
From [[Darcy's law]]:
 
From [[Darcy's law]]:
  
−
<math>\frac{q}{2}=\frac{kA}{B \mu}\ \frac{dP}{dx}</math>
+
:<math>\frac{q}{2}=\frac{kA}{\mu}\ \frac{dP}{dx}</math>
  
 +
:<math> A =y_e*h</math>
 +
 +
:<math>dP=\frac{q \mu}{2ky_eh} dx</math>
 +
 +
Integration gives: <math>P-P_{wf}=\frac{q \mu}{2ky_eh} x</math>
 +
 +
Since average pressure is: <math>\bar P = \frac{\int P dx}{\int dx}</math>
 +
 +
:<math> \bar P = \frac{ \int \limits_{0}^{x_e/2} \left ( \frac{q \mu}{2ky_eh} x + P_{wf} \right ) dx}{\int dx} = \left. \frac{q \mu}{2ky_eh} \frac{x}{2} \right|_{x=0}^{x=x_e/2} + P_{wf} = \frac{q \mu x_e}{8ky_eh} + P_{wf}</math>
 +
 +
:<math>J_D=\frac{q \mu}{2 \pi k h} \frac{1}{( \bar P - P_{wf})} =\frac{q \mu}{2 \pi k h} \frac{8ky_eh}{q \mu x_e} = \frac{4y_e}{\pi x_e}=\frac{4}{\pi}</math>
 +
 +
==See also==
 +
[[6/π stimulated well potential]]<BR/>
 +
[[JD]]<BR/>
 +
[[:Category:optiFrac | optiFrac]]<BR/>
 +
[[:Category:fracDesign | fracDesign]]<BR/>
 +
[[Production Potential]]
 +
 +
==Nomenclature==
 +
 +
:<math> A </math> = cross-sectional area, cm2
 +
:<math> h </math> = thickness, m
 +
:<math> J_D</math> = dimensionless productivity index, dimensionless
 +
:<math> k</math> = permeability, d
 +
:<math> P </math> = pressure, atm
 +
:<math> P_i </math> = initial pressure, atm
 +
:<math> \bar P</math> = average pressure, atm
 +
:<math> q </math> = flow rate, cm<sup>3</sup>/sec
 +
:<math> x </math> = length, m
 +
:<math> x_e</math> = drinage area length, m
 +
:<math> y_e</math> = drinage area width, m
 +
 +
===Greek symbols===
 +
 +
:<math> \mu </math> =viscosity, cp
  
 
[[Category:Technology]]
 
[[Category:Technology]]
 +
[[Category:pengtools]]
 
[[Category:optiFrac]]
 
[[Category:optiFrac]]
 
[[Category:optiFracMS]]
 
[[Category:optiFracMS]]
 
[[Category:fracDesign]]
 
[[Category:fracDesign]]
 +
 +
{{#seo:
 +
|title=Hydraulic fracturing formulas 4/π
 +
|titlemode= replace
 +
|keywords=hydraulic fracturing, hydraulic fracturing formulas, well potential
 +
|description=Hydraulic fracturing formulas maximum possible stimulation well potential for steady state linear flow 4/π
 +
}}

Latest revision as of 06:40, 10 December 2018

Brief

Stimulated well drainage

4/π is the maximum possible stimulation well potential for steady state linear flow in a square well spacing.

Math & Physics

Steady state flow boundary conditions:

P |_{x=x_e/2} = P |_{x=-x_e/2} = P_i
\frac{dP}{dt} =0\ for \ \forall x

From Darcy's law:

\frac{q}{2}=\frac{kA}{\mu}\ \frac{dP}{dx}
A =y_e*h
dP=\frac{q \mu}{2ky_eh} dx

Integration gives: 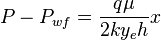P-P_{wf}=\frac{q \mu}{2ky_eh} x

Since average pressure is: 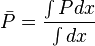\bar P = \frac{\int P dx}{\int dx}

\bar P = \frac{ \int \limits_{0}^{x_e/2} \left ( \frac{q \mu}{2ky_eh} x + P_{wf} \right ) dx}{\int dx} = \left. \frac{q \mu}{2ky_eh} \frac{x}{2} \right|_{x=0}^{x=x_e/2} + P_{wf} = \frac{q \mu x_e}{8ky_eh} + P_{wf}
J_D=\frac{q \mu}{2 \pi k h} \frac{1}{( \bar P - P_{wf})} =\frac{q \mu}{2 \pi k h} \frac{8ky_eh}{q \mu x_e} = \frac{4y_e}{\pi x_e}=\frac{4}{\pi}

See also

6/π stimulated well potential
JD
optiFrac
fracDesign
Production Potential

Nomenclature

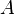A = cross-sectional area, cm2
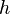h = thickness, m
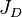J_D = dimensionless productivity index, dimensionless
k = permeability, d
P = pressure, atm
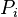P_i = initial pressure, atm
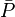\bar P = average pressure, atm
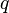q = flow rate, cm3/sec
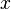x = length, m
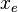x_e = drinage area length, m
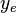y_e = drinage area width, m

Greek symbols

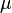\mu =viscosity, cp
Retrieved from "https://wiki.pengtools.com/index.php?title=4/π_stimulated_well_potential&oldid=5596"