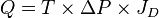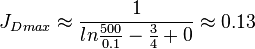Difference between revisions of "Production Potential"

From wiki.pengtools.com
Jump to: navigation, search
(→‎Math and Physics)
(→‎Maximum J_D)
 
(44 intermediate revisions by the same user not shown)
Line 4: Line 4:
  
 
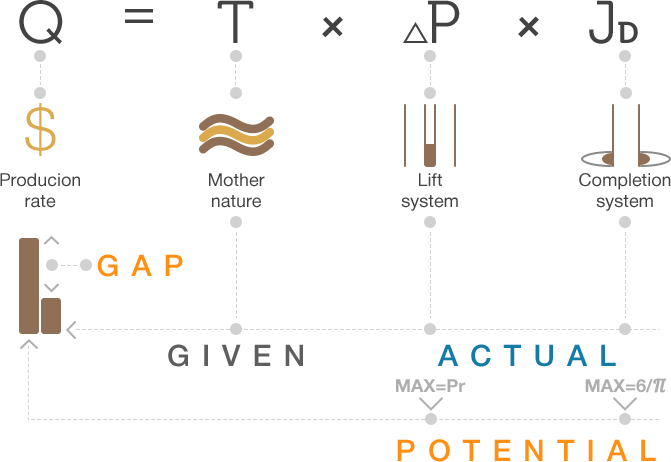
[[Production Potential]] is the '''maximum''' rate that can be delivered by [[Well]], [[Pattern]], [[Block]] or [[Reservoirs | Reservoir]].
 
[[Production Potential]] is the '''maximum''' rate that can be delivered by [[Well]], [[Pattern]], [[Block]] or [[Reservoirs | Reservoir]].
 +
 +
[[File:Production Potental.png| Production Potential]]
  
 
==Math and Physics==
 
==Math and Physics==
Line 13: Line 15:
 
where:
 
where:
  
 +
:<math>Q</math> is the oil or gas production rate,
 
:<math>T</math> is the [[Reservoirs | Reservoir]] transmissibility and is given by the [https://en.wikipedia.org/wiki/Mother_Nature Mother Nature],
 
:<math>T</math> is the [[Reservoirs | Reservoir]] transmissibility and is given by the [https://en.wikipedia.org/wiki/Mother_Nature Mother Nature],
−
:<math>\Delta P</math> is the '''Lift System''' Drawdawn which is set by the operational engineering practices,
+
:<math>\Delta P</math> is the '''Lift System''' Drawdawn which is set by the operational engineering practices<ref name=DW />,
−
:<math>J_D</math> is the '''Completion System''' dimensionless productivity index which is set by the design engineering practices.
+
:<math>J_D</math> is the '''Completion System''' dimensionless productivity index which is set by the design engineering practices<ref name=DW />.
 +
 
 +
The rate <math>Q</math> is '''maximum''' then <math>\Delta P</math> and <math>J_D</math> are '''maximum'''.
 +
 
 +
==Maximum <math>\Delta P</math>==
 +
 
 +
The drawdown is:
 +
 
 +
<math>\Delta P= \bar P_r - P_{wf}</math>
 +
 
 +
The maximum drawdown is reached then the flowing bottomhole pressure, <math>P_{wf} = 0</math>, so:
  
 +
<math>{\Delta P}_{max}= P_r</math>
  
 +
==Maximum <math>J_D</math>==
 +
The unstimulated vertical well potential in a pseudo steady radial flow is:
  
 +
:<math> {J_D}_{max} \approx \frac{1}{ln{\frac{500}{0.1}-\frac{3}{4}+0}} \approx 0.13</math>
 +
 +
The maximum possible stimulated well potential for pseudo steady linear flow is:
 +
 +
<math>{J_D}_{max}= \frac{6}{\pi} \approx 1.91 </math> , see [[6/π stimulated well potential]]
 +
 +
The maximum possible stimulated well potential for steady state linear flow is:
 +
 +
<math>{J_D}_{max}= \frac{4}{\pi} \approx 1.27 </math> , see [[4/π stimulated well potential]]
 +
 +
==Achieving potential==
 +
 +
Can [[Production Potential]] be achieved?
 +
 +
The ideal, of producing and recovering at potential, is rarely obtained in practice. [[29+ reasons why you can not increase the production |Reasons]] for this vary from company to company, but more often than not, the reason is [[Production Potential]] is not known and therefore not managed<ref name=DW />.
 +
 +
Calculating the [[Production Potential]] opens the pathway to achieve potential.
 +
 +
==See also==
 +
[[JD]]<BR/>
 +
[[6/π stimulated well potential]]<BR/>
 +
[[4/π stimulated well potential]]<BR/>
 +
 +
== References ==
 +
<references>
 +
 +
<ref name=DW>
 +
{{cite book
 +
|last1= Wolcott |first1=Don
 +
|title=Applied Waterflood Field Development
 +
|date=2009
 +
|publisher=Energy Tribune Publishing Inc
 +
|place=Houston
 +
|url=https://www.amazon.com/Applied-Waterflood-Field-Development-Wolcott/dp/0578023946/ref=sr_1_1?ie=UTF8&qid=1481788841&sr=8-1&keywords=Don+wolcott
 +
|url-access=subscription
 +
}}</ref>
 +
 +
</references>
  
−
[[File:Production Potental.png| Production Potential]]
 
  
 
[[Category:Enhancement List]]
 
[[Category:Enhancement List]]
 
[[Category:E&P Portal]]
 
[[Category:E&P Portal]]
 +
 +
{{#seo:
 +
|title=Production Potential
 +
|titlemode= replace
 +
|keywords=production potential, oil and gas production, oil production, oil and gas production optimization
 +
|description=Production Potential is the maximum rate that can be delivered through oil and gas production optimization
 +
}}

Latest revision as of 18:45, 8 July 2023

Brief

Production Potential is the maximum rate that can be delivered by Well, Pattern, Block or Reservoir.

Production Potential

Math and Physics

The Darcy's law can be written as:

Q = T \times \Delta P \times J_D

where:

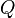Q is the oil or gas production rate,
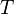T is the Reservoir transmissibility and is given by the Mother Nature,
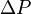\Delta P is the Lift System Drawdawn which is set by the operational engineering practices[1],
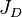J_D is the Completion System dimensionless productivity index which is set by the design engineering practices[1].

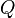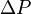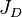The rate Q is maximum then \Delta P and J_D are maximum.

Maximum 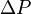\Delta P

The drawdown is:

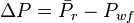
\Delta P= \bar P_r - P_{wf}

The maximum drawdown is reached then the flowing bottomhole pressure, 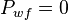P_{wf} = 0, so:

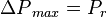
{\Delta P}_{max}= P_r

Maximum J_D

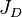
The unstimulated vertical well potential in a pseudo steady radial flow is:

{J_D}_{max} \approx \frac{1}{ln{\frac{500}{0.1}-\frac{3}{4}+0}} \approx 0.13

The maximum possible stimulated well potential for pseudo steady linear flow is:

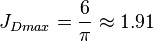{J_D}_{max}= \frac{6}{\pi} \approx 1.91 , see 6/π stimulated well potential

The maximum possible stimulated well potential for steady state linear flow is:

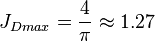{J_D}_{max}= \frac{4}{\pi} \approx 1.27 , see 4/π stimulated well potential

Achieving potential

Can Production Potential be achieved?

The ideal, of producing and recovering at potential, is rarely obtained in practice. Reasons for this vary from company to company, but more often than not, the reason is Production Potential is not known and therefore not managed[1].

Calculating the Production Potential opens the pathway to achieve potential.

See also

JD
6/π stimulated well potential
4/π stimulated well potential

References

  1. ↑ 1.0 1.1 1.2 Wolcott, Don (2009). Applied Waterflood Field DevelopmentPaid subscription required. Houston: Energy Tribune Publishing Inc. 
Retrieved from "https://wiki.pengtools.com/index.php?title=Production_Potential&oldid=7643"