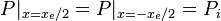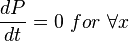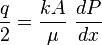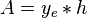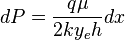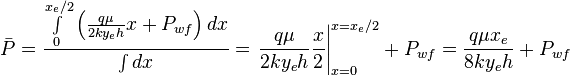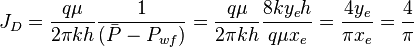4/π stimulated well potential

Brief

Stimulated well drainage

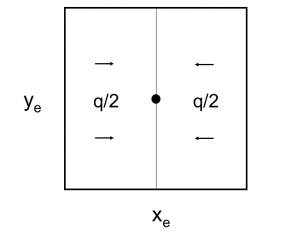
4/π is the maximum possible stimulation potential for steady state linear flow in a square well spacing.

Math & Physics

Steady state flow boundary conditions:

$P |_{x=x_e/2} = P |_{x=-x_e/2} = P_i$

$\frac{dP}{dt} =0\ for \ \forall x$

From Darcy's law:

$\frac{q}{2}=\frac{kA}{\mu}\ \frac{dP}{dx}$

$A =y_e*h$

$dP=\frac{q \mu}{2ky_eh} dx$

Integration gives: 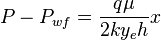$P-P_{wf}=\frac{q \mu}{2ky_eh} x$

Since average pressure is: 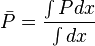$\bar P = \frac{\int P dx}{\int dx}$

$\bar P = \frac{ \int \limits_{0}^{x_e/2} \left ( \frac{q \mu}{2ky_eh} x + P_{wf} \right ) dx}{\int dx} = \left. \frac{q \mu}{2ky_eh} \frac{x}{2} \right|_{x=0}^{x=x_e/2} + P_{wf} = \frac{q \mu x_e}{8ky_eh} + P_{wf}$

$J_D=\frac{q \mu}{2 \pi k h} \frac{1}{( \bar P - P_{wf})} =\frac{q \mu}{2 \pi k h} \frac{8ky_eh}{q \mu x_e} = \frac{4y_e}{\pi x_e}=\frac{4}{\pi}$

See also

JD
optiFrac
fracDesign
Production Potential

Nomenclature

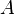$A$ = cross-sectional area, cm2

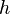$h$ = thickness, m

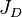$J_D$ = dimensionless productivity index, dimensionless

$k$ = permeability, d

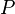$P$ = pressure, atm

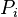$P_i$ = initial pressure, atm

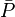$\bar P$ = average pressure, atm

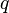$q$ = flow rate, cm³/sec

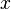$x$ = length, m

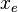$x_e$ = drinage area length, m

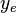$y_e$ = drinage area width, m

Greek symbols

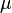$\mu$ =viscosity, cp