Difference between revisions of "Can Of Beans (Gas)"
(→Can of beans analogy) |
(→Can of beans analogy) |
||
| Line 15: | Line 15: | ||
==Can of beans analogy== | ==Can of beans analogy== | ||
| − | If you eat the can of beans fast then the can doesn’t last as long as if you eat it slow, but you still eat the same amount of beans. Same is true for the gas reservoir with bottom water. | + | If you eat the can of beans fast then the can doesn’t last as long as if you eat it slow, but you still eat the same amount of beans. |
| + | |||
| + | Same is true for the gas reservoir with bottom water. | ||
There is a fixed volume of gas above the water. When you remove the gas the water moves up. You can do it slow or fast but the volume of gas above the water is the same. The water level will raise Gravity stable as defined by Newton’s Law. | There is a fixed volume of gas above the water. When you remove the gas the water moves up. You can do it slow or fast but the volume of gas above the water is the same. The water level will raise Gravity stable as defined by Newton’s Law. | ||
Revision as of 07:20, 12 December 2022
Contents
Brief
A case study on how to increase the gas recovery factor by increasing the gas production rates.
Have you ever heard that if you increase the choke size on a gas well, the well will "die" soon, because of the water? And gas recovery will go down too?
What if you could increase the gas production and recover more gas instead?
This case study clearly demonstrates that gas recovery is increased with increasing the gas rate.
It is shown that enhanced well will add more reserves then non-enhanced well.
Case study is done using the simulation model assuring physics is well governed.
Can of beans analogy
If you eat the can of beans fast then the can doesn’t last as long as if you eat it slow, but you still eat the same amount of beans.
Same is true for the gas reservoir with bottom water.
There is a fixed volume of gas above the water. When you remove the gas the water moves up. You can do it slow or fast but the volume of gas above the water is the same. The water level will raise Gravity stable as defined by Newton’s Law.
The Power of Well Nodal Analysis
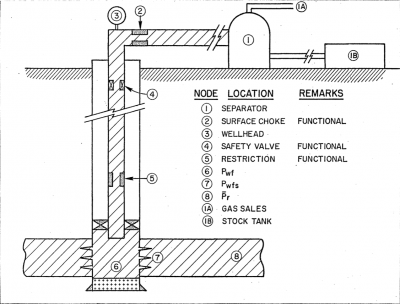
Well Nodal Analysis is the cornerstone of petroleum engineering. It allows to:
Typical Applications
Math and Physics
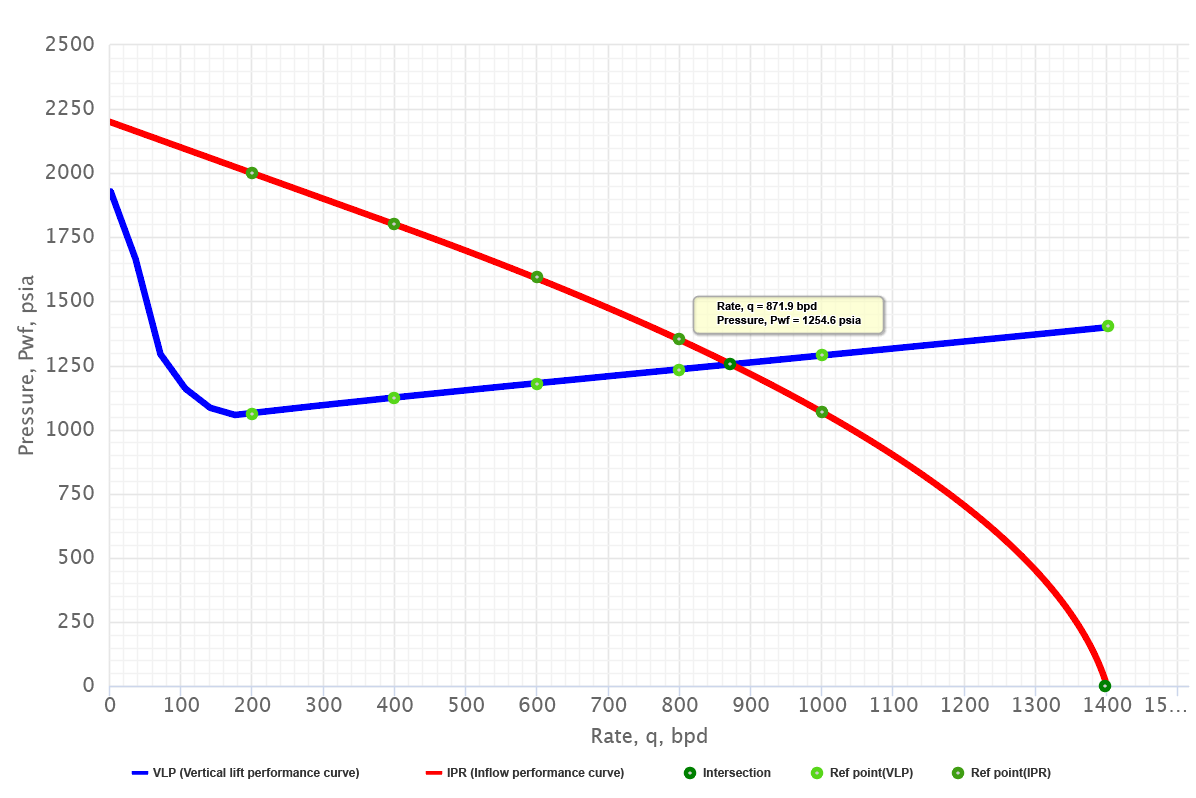
Well Nodal Analysis is done on a pressure vs rate plot. IPR and VLP curves intersect at well operating point.
Well IPR curve: Darcy's law, Vogel's IPR, Composite IPR.
Well VLP curve: Hagedorn and Brown multiphase flow correlation
Well Nodal Analysis Example
Given data[1]:
SGg=0.65, SGo=35 API, Pr=2200 psi, Pb=1800 psi, Tr=140 F, depth = 5000ft, tubing size = 2 3/8 in OD, GOR=400 scf/stb, WOR=0 Productivity index J = 1 bbl/d/psi
It's required to find the well flowing rate at the wellhead pressure of 230 psi. Surface flow line and separator are not in question.
Solution at bottom of well
In order to solve for the flow rate at bottomhole (node position 6), the entire system is divided into two components, the reservoir or well capability component, IPR and the piping system component, VLP [2].
- First, Vogel's equation is used to calculate the IPR curve. The AOF = 1400 bbl/d
| Rate, bbl/d | Pwf, psi |
|---|---|
| 0 | 2200 |
| 200 | 2000 |
| 400 | 1800 |
| 600 | 1590 |
| 800 | 1350 |
| 1000 | 1067 |
| 1400 | 0 |
- Second, Hagedorn and Brown multiphase flow correlation is used to calculate the required tubing intake pressures at the given wellhead pressure, VLP curve.
| Rate, bbl/d | Pwf, psi |
|---|---|
| 0 | 1929 |
| 200 | 1065 |
| 400 | 1125 |
| 600 | 1181 |
| 800 | 1235 |
| 1000 | 1289 |
| 1400 | 1399 |
- Third, IPR and VLP curves are plotted on the pressure vs rate plot. The intersection of these two curves shows the flow rate to be 872 bbl/d.
This is "the rate" possible for this system. It is not a maximum, minimum, or optimum but is the rate at which this well will produce for the piping system installed. The rate can be changed only by changing something in the system - that is, pipe sizes, choke or by shifting the IPR curve through simulation treatment.— Kermit Brown et al [2]
See also
References
- ↑ 1.0 1.1
Mach, Joe; Proano, Eduardo; Brown, Kermit E. (1979). "A Nodal Approach For Applying Systems Analysis To The Flowing And Artificial Lift Oil Or Gas Well"
 (SPE-8025-MS). Society of Petroleum Engineers.
(SPE-8025-MS). Society of Petroleum Engineers.
- ↑ 2.0 2.1 Brown, Kermit (1984). The Technology of Artificial Lift Methods. Volume 4. Production Optimization of Oil and Gas Wells by Nodal System Analysis. Tulsa, Oklahoma: PennWellBookss.
Cite error: <ref> tag with name "Legends" defined in <references> is not used in prior text.