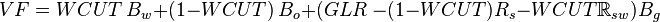Difference between revisions of "3 Phase IPR"

Revision as of 07:00, 17 April 2019

Three-phase Inflow Performance Relationship

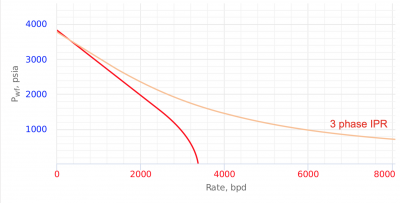
3 Phase IPR Curve ^[1]

3 Phase IPR is an IPR curve calculated on the basis of total barrels of produced fluid, including gas.

3 Phase IPR curve is used in Pump Design software for pump sizing.

Math and Physics

The volume of 1 stb of liquid plus associated gas at any pressure and temperature is given by^[1]:

VF=WCUT\ B_w + (1-WCUT)\ B_o + (GLR\ - (1-WCUT)R_s - WCUT\R_{sw})B_g

^[1]

3 Phase IPR calculation example

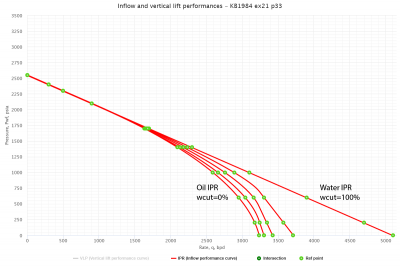
Figure.1 3 Phase IPR calculation example

Following the example problem #21, page 33 ^[1]:

Given:

P_r

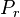= 2550 psi

P_b

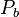= 2100 psi

Test data:

P_{wf}

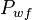= 2300 psi

q_t

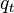= 500 b/d

Calculate:

Determine the 3 Phase IPR curves for F_w=0, 0.25, 0.5, 0.75, and 1.

Solution:

The problem was run through PQplot software for different values of watercut.

Result 3 Phase IPR curves are shown on Fig.1. Points indicate results obtained by Brown ^[1].

The PQplot model from this example is available online by the following link: 3 Phase IPR calculation example

Nomenclature

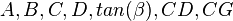A, B, C, D, tan(\beta), CD, CG

= calculation variables

F_o

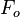= oil fraction, fraction

F_w

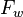= water fraction, fraction

J

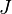= productivity index, stb/d/psia

P

= pressure, psia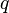

q

= flowing rate, stb/d

Subscripts

b = at bubble point

max = maximum

o = oil

r = reservoir

t = total

wf = well flowing bottomhole pressure

wfG = well flowing bottomhole pressure at point G

References

↑ ^1.0 ^1.1 ^1.2 ^1.3 ^1.4 Brown, Kermit (1984). The Technology of Artificial Lift Methods. Volume 4. Production Optimization of Oil and Gas Wells by Nodal System Analysis. Tulsa, Oklahoma: PennWellBookss.

@@ Line 8: / Line 8: @@
 ==Math and Physics==
-Total flow rate equations:
+The volume of 1 stb of liquid plus associated gas at any pressure and temperature is given by<ref name=KermitBrown1984/>:
-===For P<sub>b</sub> < P<sub>wf</sub> < P<sub>r</sub>===
+:<math> VF=WCUT\ B_w + (1-WCUT)\ B_o + (GLR\ - (1-WCUT)R_s - WCUT\R_{sw})B_g</math> <ref name=KermitBrown1984/>
-For pressures between reservoir pressure and bubble point pressure:
-:<math> q_t =J (P_r - P_{wf})</math> <ref name=KermitBrown1984/>
-===For P<sub>wfG</sub> < P<sub>wf</sub> < P<sub>b</sub>===
-For pressures between the bubble point pressure and the flowing bottom-hole pressures:
-:<math> q_t =\frac{-C+\sqrt{C^2-4B^2D}}{2B^2}\ for B \ne 0</math><ref name=KermitBrown1984/>
-:<math> q_t =D/C\ for B = 0</math><ref name=KermitBrown1984/>
-where:
-:<math> A=\frac{P_{wf}+0.125F_oP_b-F_wP_r}{0.125F_oP_b}</math><ref name=KermitBrown1984/>
-:<math> B=\frac{F_w}{0.125F_oP_bJ}</math><ref name=KermitBrown1984/>
-:<math> C=2AB+\frac{80}{q_{o_{max}}-q_b}</math><ref name=KermitBrown1984/>
-:<math> D=A^2-80\frac{q_b}{q_{o_{max}}-q_b}-81</math><ref name=KermitBrown1984/>
-=== For 0 < P<sub>wf</sub> < P<sub>wfG</sub>===
-:<math> q_t =\frac{P_{wfG}+q_{o_{max}}tan(\beta)-P_{wf}}{tan(\beta)}</math><ref name=KermitBrown1984/>
-where:
-:<math> tan(\beta) = CD/CG </math><ref name=KermitBrown1984/>
-:<math> CD = F_w\frac{0.001q_{o_{max}}}{J}+F_o0.125P_b \left ( -1+\sqrt{81-80 \frac{0.999q_{o_{max}}-q_b}{q_{o_{max}}-q_b}} \right)</math><ref name=KermitBrown1984/>
-:<math> CG = 0.001 q_{o_{max}}</math><ref name=KermitBrown1984/>
-===And===
-:<math> P_{wfG}=F_w \left ( P_r - \frac{q_{o_{max}}}{J}\right )</math><ref name=KermitBrown1984/>
-:<math> q_{o_{max}}=q_b+\frac{JP_b}{1.8}</math><ref name=KermitBrown1984/>
 ==[[3 Phase IPR]] calculation example==

Navigation menu

Navigation

Categories

Products