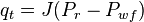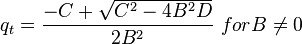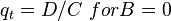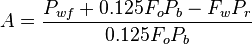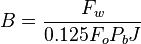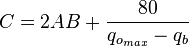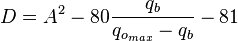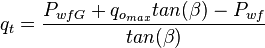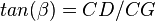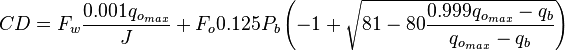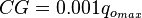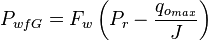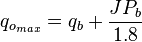Difference between revisions of "3 Phase IPR"

From wiki.pengtools.com
Jump to: navigation, search
(→‎See also)
(→‎3 Phase IPR calculation example)
Line 42: Line 42:
  
 
==[[3 Phase IPR]] calculation example==
 
==[[3 Phase IPR]] calculation example==
−
*[[:Category:PQplot | PQplot]] nodal analysis software is used to calculate the [[IPR]] curves. [[:Category:PQplot | PQplot]]  is available online at [https://www.pengtools.com www.pengtools.com].
+
Following the example problem #21, page 33 <ref name=KermitBrown1984 />:
−
*Excel
 
−
*other
 
  
 
== Nomenclature  ==
 
== Nomenclature  ==

Revision as of 09:12, 11 April 2019

Three-phase Inflow Performance Relationship

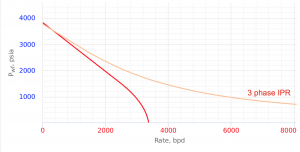
3 Phase IPR Curve [1]

3 Phase IPR calculates IPR curve for oil wells producing water at various watercuts.

3 Phase IPR equation was derived by Petrobras based on combination of Vogel's IPR equation for oil flow and constant productivity for water flow [1].

3 Phase IPR curve is determined geometrically from those equations considering the fractional flow of oil and water [1].

Math and Physics

Total flow rate equations:

For Pb < Pwf < Pr

For pressures between reservoir pressure and bubble point pressure:

q_t =J (P_r - P_{wf}) [1]

For PwfG < Pwf < Pb

For pressures between the bubble point pressure and the flowing bottom-hole pressures:

q_t =\frac{-C+\sqrt{C^2-4B^2D}}{2B^2}\ for B \ne 0[1]
q_t =D/C\ for B = 0[1]

where:

A=\frac{P_{wf}+0.125F_oP_b-F_wP_r}{0.125F_oP_b}[1]
B=\frac{F_w}{0.125F_oP_bJ}[1]
C=2AB+\frac{80}{q_{o_{max}}-q_b}[1]
D=A^2-80\frac{q_b}{q_{o_{max}}-q_b}-81[1]

For 0 < Pwf < PwfG

q_t =\frac{P_{wfG}+q_{o_{max}}tan(\beta)-P_{wf}}{tan(\beta)}[1]

where:

tan(\beta) = CD/CG [1]
CD = F_w\frac{0.001q_{o_{max}}}{J}+F_o0.125P_b \left ( -1+\sqrt{81-80 \frac{0.999q_{o_{max}}-q_b}{q_{o_{max}}-q_b}} \right)[1]
CG = 0.001 q_{o_{max}}[1]

And

P_{wfG}=F_w \left ( P_r - \frac{q_{o_{max}}}{J}\right )[1]
q_{o_{max}}=q_b+\frac{JP_b}{1.8}[1]

3 Phase IPR calculation example

Following the example problem #21, page 33 [1]:

Nomenclature

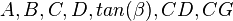A, B, C, D, tan(\beta), CD, CG = calculation variables
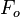F_o = oil fraction, fraction
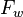F_w = water fraction, fraction
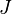J = productivity index, stb/d/psia
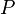P = pressure, psia
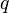q = flowing rate, stb/d

Subscripts

b = at bubble point
max = maximum
o = oil
r = reservoir
t = total
wf = well flowing bottomhole pressure
wfG = well flowing bottomhole pressure at point G

References

  1. ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 1.12 1.13 1.14 1.15 1.16 Brown, Kermit (1984). The Technology of Artificial Lift Methods. Volume 4. Production Optimization of Oil and Gas Wells by Nodal System Analysis. Tulsa, Oklahoma: PennWellBookss. 

See also

IPR
Vogel's IPR
Darcy's law
Retrieved from "https://wiki.pengtools.com/index.php?title=3_Phase_IPR&oldid=6097"