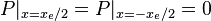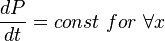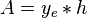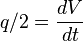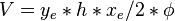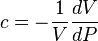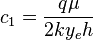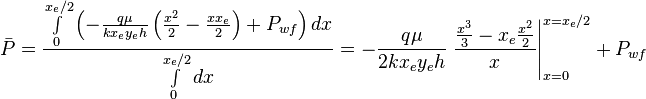Difference between revisions of "6/π stimulated well potential"

From wiki.pengtools.com
Jump to: navigation, search
(→‎Math & Physics)
(→‎Math & Physics)
Line 52: Line 52:
 
Since average pressure is: <math>\bar P = \frac{\int P dx}{\int dx}</math>:
 
Since average pressure is: <math>\bar P = \frac{\int P dx}{\int dx}</math>:
  
−
:<math> \bar P = \frac{ \int \limits_{0}^{x_e/2} \left ( - \frac{q \mu}{k x_e y_e h} \left ( \frac{x^2}{2} - \frac{x x_e}{2} \right ) +  P_{wf} \right ) dx}{\int  \limits_{0}^{x_e/2}dx} = - \frac{q \mu}{2 k x_e y_e h} \frac{\frac{x_3}{3} - x_e \frac{x_2}{2}}{x}</math>
+
:<math> \bar P = \frac{ \int \limits_{0}^{x_e/2} \left ( - \frac{q \mu}{k x_e y_e h} \left ( \frac{x^2}{2} - \frac{x x_e}{2} \right ) +  P_{wf} \right ) dx}{\int  \limits_{0}^{x_e/2}dx} = - \frac{q \mu}{2 k x_e y_e h} \left. \frac{\frac{x^3}{3} - x_e \frac{x^2}{2}}{x} \right|_{x=0}^{x=x_e/2} +  P_{wf} </math>
  
 
==Diff eq==
 
==Diff eq==

Revision as of 10:15, 12 September 2018

Brief

Stimulated well drainage

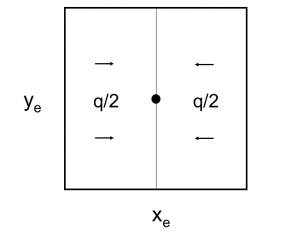
6/π is the maximum possible stimulation potential for pseudo steady state linear flow in a square well spacing.

Math & Physics

Pseudo steady state flow boundary conditions:

P |_{x=x_e/2} = P |_{x=-x_e/2} = 0
\frac{dP}{dt} =const\ for \ \forall x

From Diffusivity Equation:

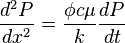\frac{d^2P}{dx^2}=\frac{\phi c \mu}{k} \frac{dP}{dt} ( 1 )

From Darcy's law:

\frac{q}{2}=\frac{kA}{\mu}\ \frac{dP}{dx}
A =y_e*h

From Material Balance:

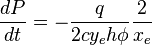q/2 =\frac{dV}{dt}
V =y_e*h*x_e/2*\phi
c=-\frac{1}{V} \frac{dV}{dP}
\frac{dP}{dt} = -\frac{q}{2 c y_e h \phi} \frac{2}{x_e} ( 2 )

( 2 ) - > ( 1 ) :

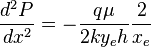\frac{d^2P}{dx^2}=- \frac{q \mu}{2 k y_e h} \frac{2}{x_e} ( 3 )

Integrating ( 3 ):

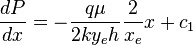\frac{dP}{dx}=- \frac{q \mu}{2 k y_e h} \frac{2}{x_e} x + c_1 ( 3 )
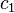c_1 must satisfy boundary condition:
c_1 = \frac{q \mu}{2 k y_e h}
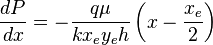\frac{dP}{dx}=- \frac{q \mu}{k x_e y_e h} \left ( x- \frac{x_e}{2} \right ) ( 4 )

Integrating ( 4 ):

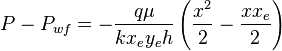P - P_{wf} = - \frac{q \mu}{k x_e y_e h} \left ( \frac{x^2}{2} - \frac{x x_e}{2} \right ) ( 5 )

Since average pressure is: 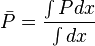\bar P = \frac{\int P dx}{\int dx}:

\bar P = \frac{ \int \limits_{0}^{x_e/2} \left ( - \frac{q \mu}{k x_e y_e h} \left ( \frac{x^2}{2} - \frac{x x_e}{2} \right ) + P_{wf} \right ) dx}{\int \limits_{0}^{x_e/2}dx} = - \frac{q \mu}{2 k x_e y_e h} \left. \frac{\frac{x^3}{3} - x_e \frac{x^2}{2}}{x} \right|_{x=0}^{x=x_e/2} + P_{wf}

Diff eq

From Mass conservation:

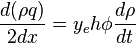\frac{d(\rho q)}{2 dx}=y_e h \phi \frac{d\rho}{dt} ( 1 )

From Darcy's law:

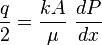\frac{q}{2}=\frac{kA}{\mu}\ \frac{dP}{dx} ( 2 )
A =y_e*h

( 2 ) →( 1 ):

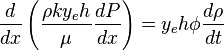\frac{d}{dx} \left ( \frac{\rho k y_e h}{\mu} \frac{dP}{dx} \right )=y_e h \phi \frac{d\rho}{dt} ( 3 )
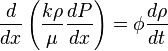\frac{d}{dx} \left ( \frac{k \rho}{\mu} \frac{dP}{dx} \right )=\phi \frac{d\rho}{dt} ( 4 )
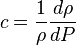c=\frac{1}{\rho} \frac{d \rho}{dP} ( 5 )

( 5 ) -> ( 4 ):

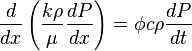\frac{d}{dx} \left ( \frac{k \rho}{\mu} \frac{dP}{dx} \right )=\phi c \rho \frac{dP}{dt} ( 6 )
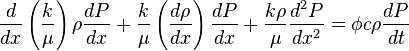\frac{d}{dx} \left ( \frac{k}{\mu} \right ) \rho \frac{dP}{dx} + \frac{k}{\mu} \left ( \frac{d \rho}{dx} \right ) \frac{dP}{dx} + \frac{k \rho}{\mu} \frac{d^2P}{dx^2}=\phi c \rho \frac{dP}{dt} ( 7 )

Assumption that viscosity is constant cancels out first term in left hand side of (7):

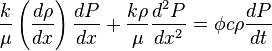\frac{k}{\mu} \left ( \frac{d \rho}{dx} \right ) \frac{dP}{dx} + \frac{k \rho}{\mu} \frac{d^2P}{dx^2}=\phi c \rho \frac{dP}{dt} ( 8 )
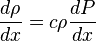\frac{d \rho}{dx} = c \rho \frac{d P}{dx} ( 9 )

( 9 ) -> ( 8 ):

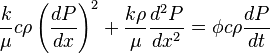\frac{k}{\mu} c \rho \left ( \frac{dP}{dx} \right )^2+ \frac{k \rho}{\mu} \frac{d^2P}{dx^2}=\phi c \rho \frac{dP}{dt} ( 10 )

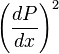Term \left ( \frac{dP}{dx} \right )^2 in (10) is second order of magnitude low and can be cancelled out, which yields:


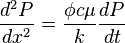\frac{d^2P}{dx^2}=\frac{\phi c \mu}{k} \frac{dP}{dt} ( 11 )

See also

optiFrac
fracDesign
Production Potential

Nomenclature

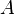A = cross-sectional area, cm2
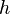h = thickness, m
k = permeability, d
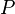P = pressure, atm
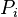P_i = initial pressure, atm
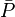\bar P = average pressure, atm
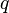q = flow rate, cm3/sec
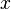x = length, m
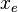x_e = drinage area length, m
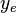y_e = drinage area width, m

Greek symbols

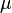\mu = oil viscosity, cp
Retrieved from "https://wiki.pengtools.com/index.php?title=6/π_stimulated_well_potential&oldid=4764"