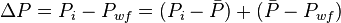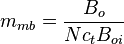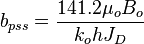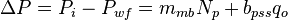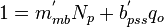Difference between revisions of "Reciprocal Rate Method"
(→Nomenclature) |
(→Nomenclature) |
||
| Line 86: | Line 86: | ||
:<math> B_{o} </math> = oil formation volume factor, bbl/stb | :<math> B_{o} </math> = oil formation volume factor, bbl/stb | ||
| + | :<math> B_{oi} </math> = initial oil formation volume factor, bbl/stb | ||
:<math> b_{pss} </math> = reservoir constant, inverse to productivity index, psia/stb/d | :<math> b_{pss} </math> = reservoir constant, inverse to productivity index, psia/stb/d | ||
:<math> c_t </math> = total compressibility, psia<sup>-1</sup> | :<math> c_t </math> = total compressibility, psia<sup>-1</sup> | ||
Revision as of 20:56, 28 May 2018
Contents
Brief
Reciprocal Rate Method - is the method to estimate oil Wells and Reservoirs EUR using only rate-time production data[1] published in 2007 by Thomas Blasingame et al.
The methodology does presume that flowing well bottomhole pressures are approximately constant[1].
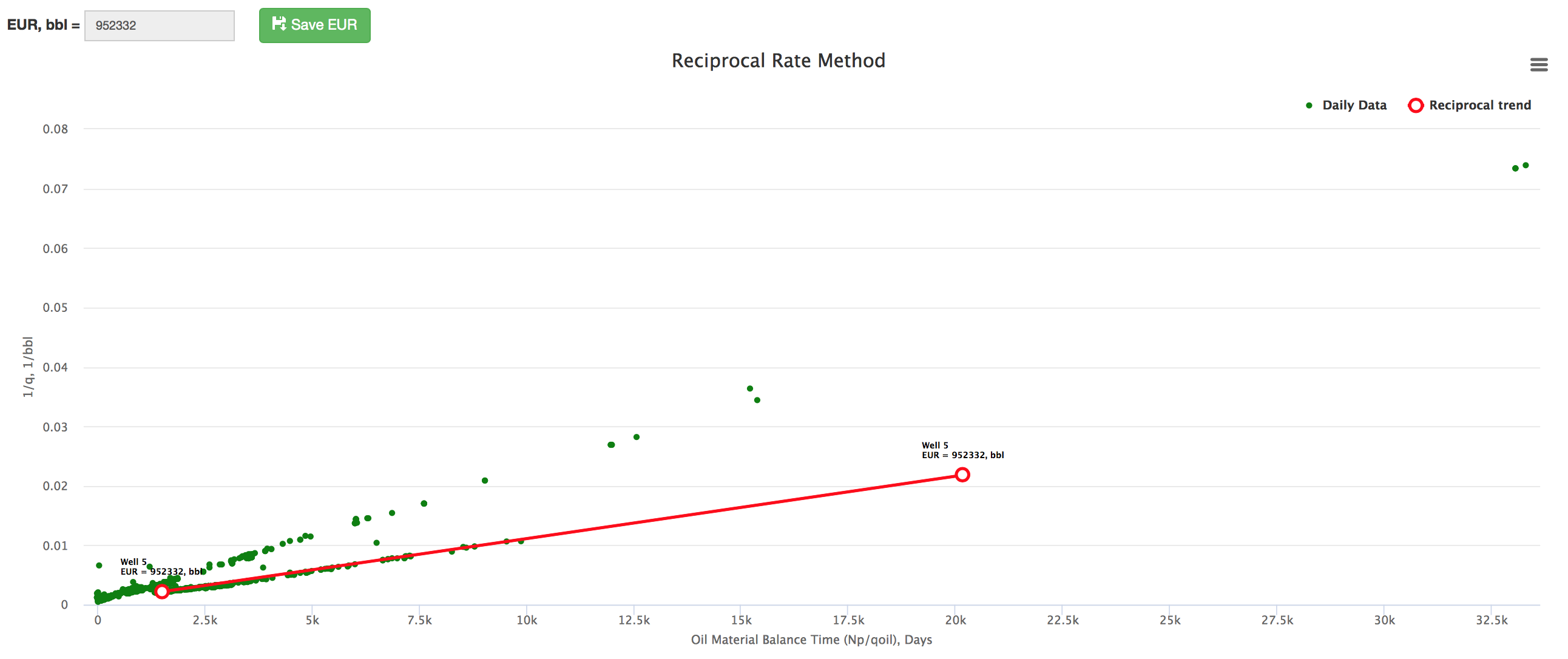
The interpretation technique is fitting the data points with the straight line to estimate the slope which gives EUR.
Math & Physics
The total pressure drop at the wellbore is:
Where:
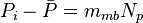 , is pressure drop due to depletion defined by the Oil Material Balance for black oil at P>Pb,
, is pressure drop due to depletion defined by the Oil Material Balance for black oil at P>Pb,
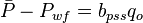 , is pressure drop due to Darcy's law
, is pressure drop due to Darcy's law
Where:
The total pressure drop at the wellbore now can be rewritten as:
Dividing both sides by the assumed constant: 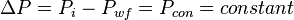 [1]:
[1]:
As the flowrate decreases to zero (i.e., qo → 0)[1]:
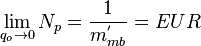
Therefore a plot of 1/qo versus Np/qo yields a straight-line trend where the slope of the line is inversely proportional to the EUR[1].
Discussion
Reciprocal Rate Method can be applied to estimate:
Case Study
This Case Study demonstrates the application of the Oil Flowing Material Balance engineering technique using the E&P Portal.
The Study is based on the oil well from a field in West Siberia, Russia.
It is shown how to:
- Input the data to the E&P Portal;
- Apply the Oil FMB to estimate the well's STOIIP and JD;
- Save and export the analysis results.
All the input data is attached to the Case Study for the reference.
Download the input well production data (csv)
Workflow
- Upload the data required
- Open the Oil Flowing Material Balance tool here
- Estimate the N (red line X-axis intercept)
- Calculate the average reservoir pressure
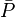 based on N, known production data and using Oil Material Balance equation
based on N, known production data and using Oil Material Balance equation - Calculate the
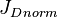
- Calculate the
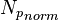
- Plot the orange
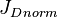 vs
vs 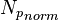 line:
line: - Change the N to match the orange line with the red one
- Change the gray JD line Y-axis intercept to match the changing JD
- Save the Oil Flowing Material Balance model
- Move to the next well
Data required
- Create Field here
- Create or Upload Reservoirs here
- Input the Reservoirs GIIP and STOIIP here
- Create or Upload PVT (SG, Pi, Ti) here
- Upload Wells
- Create or Upload Wells Perforations here
- Create or Upload kh and JD here
- Upload Daily Measures
In case you need to calculate the flowing bottomhole pressure from the wellhead pressure:
- Calculate the flowing bottomhole pressures using BHP Calculator
- Export flowing bottomhole pressures to Daily Measures here
In case you want to add the static reservoir pressures on the FMB Plot:
- Create or Upload the static reservoir pressures, here
- Calculate Monthly Measures from the Daily Measures using Monthly Data Calculator
Nomenclature
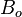 = oil formation volume factor, bbl/stb
= oil formation volume factor, bbl/stb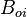 = initial oil formation volume factor, bbl/stb
= initial oil formation volume factor, bbl/stb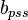 = reservoir constant, inverse to productivity index, psia/stb/d
= reservoir constant, inverse to productivity index, psia/stb/d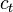 = total compressibility, psia-1
= total compressibility, psia-1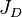 = dimensionless productivity index, dimensionless
= dimensionless productivity index, dimensionless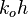 = oil permeability times thickness, md*ft
= oil permeability times thickness, md*ft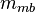 = slope term, psia/stb
= slope term, psia/stb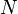 = stock tank oil initially in place, stb
= stock tank oil initially in place, stb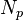 = cumulative oil production, stb
= cumulative oil production, stb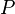 = pressure, psia
= pressure, psia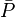 = average reservoir pressure, psia
= average reservoir pressure, psia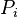 = initial pressure, psia
= initial pressure, psia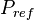 = reference pressure, psia
= reference pressure, psia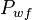 = well flowing pressure, psia
= well flowing pressure, psia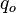 = oil rate, stb/d
= oil rate, stb/d
Greek symbols
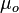 = oil viscosity , cp
= oil viscosity , cp