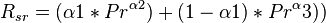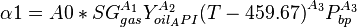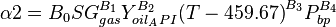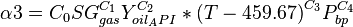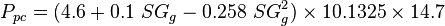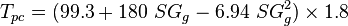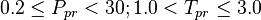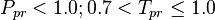Difference between revisions of "Velarde solution gas oil ratio correlation"
From wiki.pengtools.com
Gprotsykov (talk | contribs) (Created page with "__TOC__ === Brief === Velarde correlation is the fitting equation of the classic '''Standing and Katz''' <ref name=Standing&Katz /> gas compressibility factor correlatio...") |
Gprotsykov (talk | contribs) |
||
| Line 18: | Line 18: | ||
A4 = 1.056052<br/> | A4 = 1.056052<br/> | ||
| − | :<math> \alpha1 = A0 * SG^{A_1}_{gas} | + | :<math> \alpha1 = A0 * SG^{A_1}_{gas} Y^{A_2}_{oil_API} {(T- 459.67)}^{A_3} P^{A_3}_{bp} </math> |
B0 = 0.1004<br/> | B0 = 0.1004<br/> | ||
| Line 26: | Line 26: | ||
B4 = 0.302065<br/> | B4 = 0.302065<br/> | ||
| − | :<math>\alpha2 = B_0 SG^{B_1}_{gas} | + | :<math>\alpha2 = B_0 SG^{B_1}_{gas} Y^{B_2}_{oil_API} {(T - 459.67)}^{B_3} P^{B_4}_{bp}</math> |
C0 = 0.9167<br/> | C0 = 0.9167<br/> | ||
| Line 34: | Line 34: | ||
C4 = 0.047094<br/> | C4 = 0.047094<br/> | ||
| − | :<math>\ | + | :<math>\alpha3 = C_0 SG^{C_1}_{gas} Y^{C_2}_{oil_API} *{(T - 459.67)}^{C_3} P^{C_4}_{bp}</math> |
<ref name= Dranchuk/> | <ref name= Dranchuk/> | ||
Revision as of 08:18, 8 June 2017
Contents
Brief
Velarde correlation is the fitting equation of the classic Standing and Katz [1] gas compressibility factor correlation.
Math & Physics
where:
A0 = 1.8653e-4
A1 = 1.672608
A2 = 0.929870
A3 = 0.247235
A4 = 1.056052
B0 = 0.1004
B1 = -1.00475
B2 = 0.337711
B3 = 0.132795
B4 = 0.302065
C0 = 0.9167
C1 = -1.48548
C2 = -0.164741
C3 = -0.09133
C4 = 0.047094
Discussion
Why the Velarde correlation?
Workflow
To solve the Dranchuk equation use the iterative secant method.
To find the pseudo critical properties from the gas specific gravity [1]:
Application range
and
Nomenclature
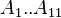 = coefficients
= coefficients = reduced density, dimensionless
= reduced density, dimensionless = pressure, psia
= pressure, psia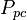 = pseudo critical pressure, psia
= pseudo critical pressure, psia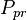 = pseudoreduced pressure, dimensionless
= pseudoreduced pressure, dimensionless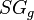 = gas specific gravity, dimensionless
= gas specific gravity, dimensionless = temperature, °R
= temperature, °R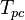 = pseudo critical temperature, °R
= pseudo critical temperature, °R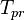 = pseudoreduced temperature, dimensionless
= pseudoreduced temperature, dimensionless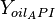 = oil API gravity, dimensionless
= oil API gravity, dimensionless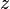 = gas compressibility factor, dimensionless
= gas compressibility factor, dimensionless
References
- ↑ 1.0 1.1 Standing, M. B.; Katz, D. L. (December 1942). "Density of Natural Gases"
 . Transactions of the AIME. Society of Petroleum Engineers. 146 (SPE-942140-G).
. Transactions of the AIME. Society of Petroleum Engineers. 146 (SPE-942140-G).
- ↑ 2.0 2.1 2.2 Dranchuk, P. M.; Abou-Kassem, H. (July 1975). "Calculation of Z Factors For Natural Gases Using Equations of State"
 . The Journal of Canadian Petroleum. 14 (PETSOC-75-03-03).
. The Journal of Canadian Petroleum. 14 (PETSOC-75-03-03).