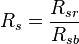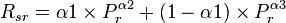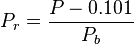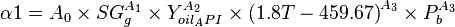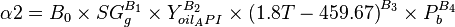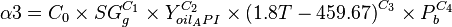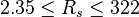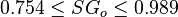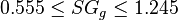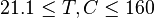Velarde solution gas oil ratio correlation
From wiki.pengtools.com
(Redirected from Velarde correlation)
Contents
Velarde solution gas oil ratio correlation
Velarde solution gas oil ratio correlation is an empirical correlation for the solution gas oil ratio published in 1997. [1]
Math & Physics
where:
A0 = 1.8653e-4[2]
A1 = 1.672608
A2 = 0.929870
A3 = 0.247235
A4 = 1.056052
B0 = 0.1004[2]
B1 = -1.00475
B2 = 0.337711
B3 = 0.132795
B4 = 0.302065
C0 = 0.9167[2]
C1 = -1.48548
C2 = -0.164741
C3 = -0.09133
C4 = 0.047094
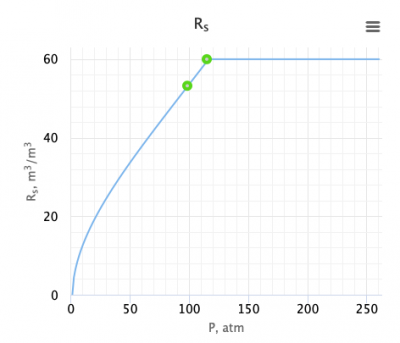
Example. Calculation of the solution gas oil ratio
Example source [3]
Input data
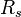 = 60 sm3/sm3
= 60 sm3/sm3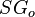 = 0.85 or 35 API
= 0.85 or 35 API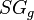 = 0.75
= 0.75 = 90C or 363K
= 90C or 363K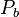 = 11.65 MPa
= 11.65 MPa
Calculate solution gas oil ratio at p = 10 MPa?
Solution
Pr = 0.8493
a1=0.1545
a2=1.8812
a3=0.5431
Rsr=0.8874
Rs=53.24 sm3/sm3
The solution is available in the online PVT calculator software at www.pengtools.com
Application range
Nomenclature
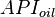 = oil specific gravity, °R
= oil specific gravity, °R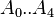 = coefficients
= coefficients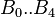 = coefficients
= coefficients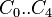 = coefficients
= coefficients = pressure, MPa
= pressure, MPa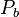 = bubble point pressure, MPa
= bubble point pressure, MPa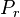 = reduced pressure, MPa
= reduced pressure, MPa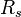 = solution oil gas ratio, sm3/sm3
= solution oil gas ratio, sm3/sm3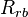 = solution oil gas ratio at bubble point pressure, sm3/sm3
= solution oil gas ratio at bubble point pressure, sm3/sm3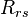 = reduced solution oil gas ratio, sm3/sm3
= reduced solution oil gas ratio, sm3/sm3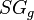 = gas specific gravity, dimensionless
= gas specific gravity, dimensionless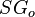 = oil specific gravity, dimensionless
= oil specific gravity, dimensionless = temperature, °K
= temperature, °K
References
- ↑
Velarde, J.; Blasingame, T. A.; McCain Jr., W. D. (1997). "Correlation of Black Oil Properties At Pressures Below Bubble Point Pressure - A New Approach"
 . Presented at the Annual Technical Meeting of CIM, Calgary, Alberta. Petroleum Society of Canada (PETSOC-97-93).
. Presented at the Annual Technical Meeting of CIM, Calgary, Alberta. Petroleum Society of Canada (PETSOC-97-93).
- ↑ 2.0 2.1 2.2 Afanasyev, Vitaliy; Moskvin, Igor; Wolcott, Ken; McCain, W.D. (2004). "Practical PVT Calculations for black oils". YUKOS publication.
- ↑
Wolcott, Don (2009). Applied Waterflood Field Development
 . Houston: Energy Tribune Publishing Inc.
. Houston: Energy Tribune Publishing Inc.