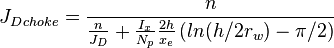Difference between revisions of "Category: OptiFracMS"

Revision as of 08:28, 12 November 2019

1 Multistage Fracturing Software
2 Typical applications
3 Math & Physics
4 Type Curves
- 4.1 Modification to rectangular (nonsquare) drainage areas
5 Physical Constraints
- 5.1 Choke skin
- 5.2 Minimum fracture width constraint
6 Flow Diagram
7 Workflow
8 Case Study
9 Main features
10 Interface features
11 References

Multistage Fracturing Software

pengtools optiFracMS

optiFracMS is a software to optimize the number of hydraulic fractures in horizontal well ^[1].

For the given set of reservoir properties and the proppant mass optiFracMS calculates optimal number of transverse hydraulic fractures and required fractures geometry to maximize well productivity index.

optiFracMS is available online at www.pengtools.com.

Typical applications

Multistage Fracturing Design in tight oil and gas reservoirs
- How many fractures are required to maximize production?
  - Number of fractures, n.
- What fractures geometry is required to maximize production?
  - Dimensionless Fracture conductivity, C_fD .
  - Fracture half length, X_f .
  - Fracture width, w .
  - Fracture penetration, I_x .
- What would be the optimal productivity index?
  - Dimensionless productivity index, J_D .
Multistage Post fracture performance reviews
- Find out how far your well's productivity from where it should be (from the optimum)
Multistage Fracturing Sensitivity Studies and Benchmarking

Math & Physics

Horizontal well with multiple transverse fractures in a rectangular drainage area

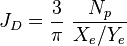J_D=\frac{3}{\pi}\ \frac{N_p}{X_e/Y_e}

- technical potential for multistage fracturing ^[1],

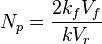N_p=\frac{2 k_f V_f}{k V_r}

- proppant number,

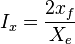I_x=\frac{2x_f}{X_e}

- penetration ratio,

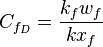C_{f_D}=\frac{k_f w_f}{k x_f}

- dimensionless fracture conductivity,

Type Curves

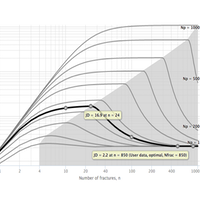
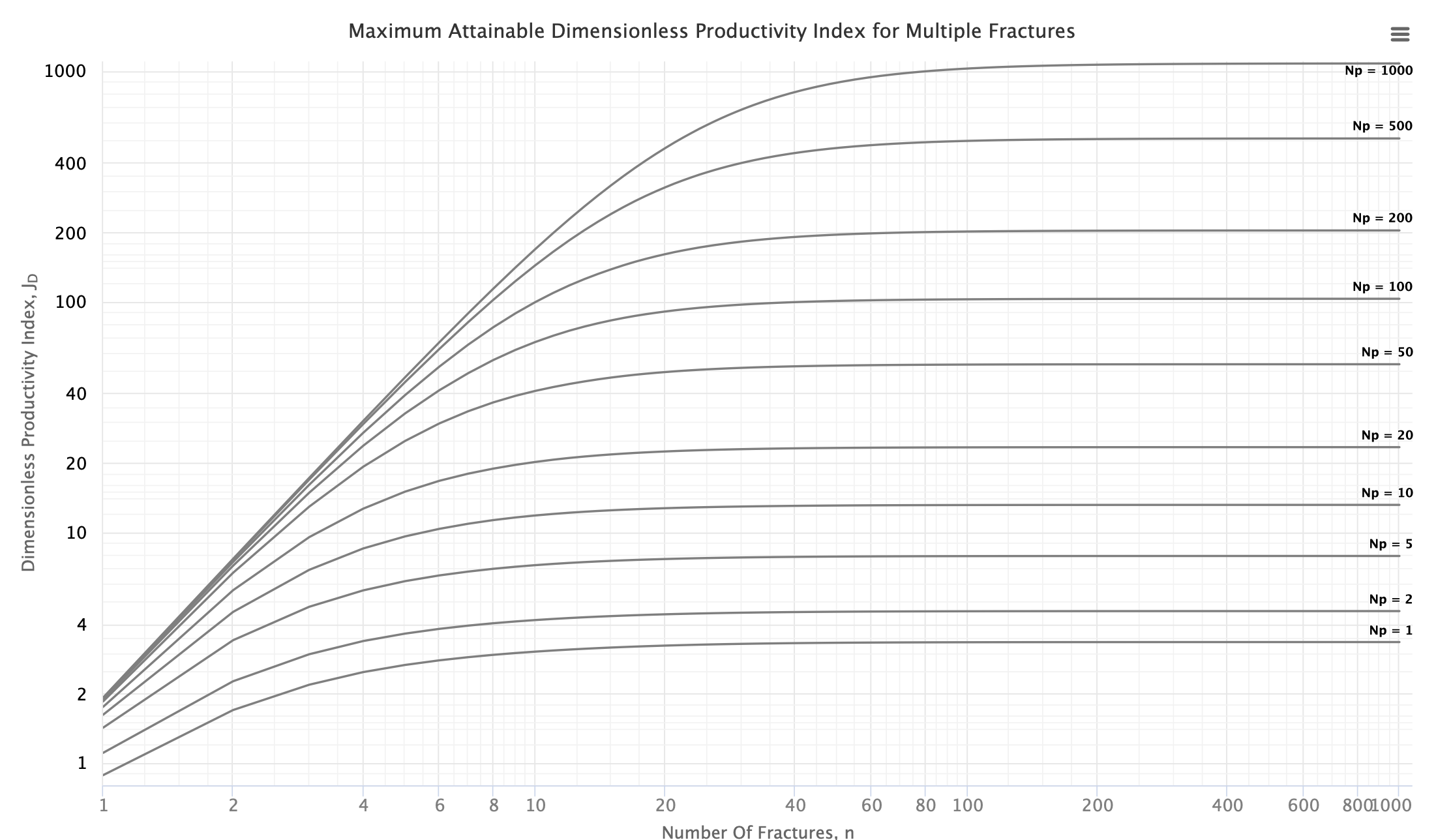
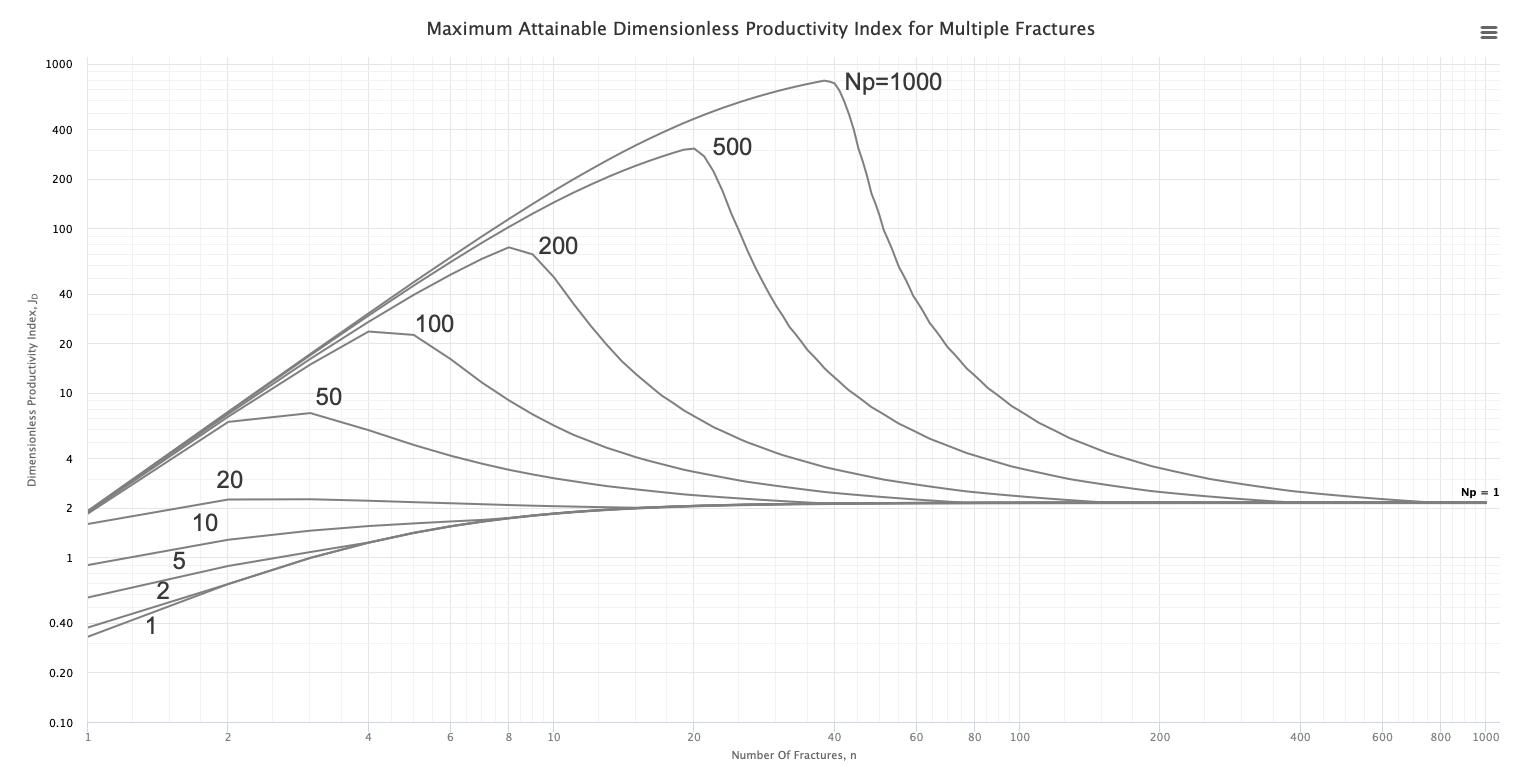
The type curves show multistage fracturing dimensionless productivity index, J_D , at pseudo-steady state as a function of number of fractures, n and proppant number, N_p for a horizontal well with multiple transverse hydraulic fractures in a square drainage area.

Type Curves were obtained, through 28,000 runs with direct boundary element (DBE) method ^[1].

For the given proppant number, N_p, the more fractures that are created the higher the well J_D. This is achieved by increasing the number of fractures, n, at the expense of individual fracture half-length and/or width. However, at some point, the additional increase in the number of fractures will result in fractures that are too slim to be practical. Such constrain is addressed below.

These type curves are also applicable for the case of rectangular (nonsquare) drainage areas.

Modification to rectangular (nonsquare) drainage areas

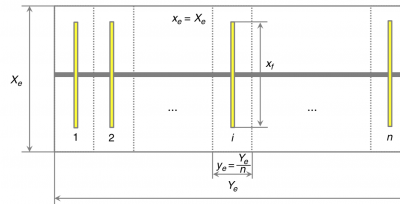
The modification needed for a rectangular well drainage is to divide both number of fractures and the corresponding JD by (Xe/Ye) ^[1].

Physical Constraints

Choke skin

Choke skin is defined as the additional pressure loss because of convergence of flow in the vertical fracture to the horizontal wellbore.

Choke skin can be calculated as follows:

{J_D}_{choke}= \frac{n}{\frac{n}{J_D}+\frac{I_x}{N_p} \frac{2h}{x_e} \left ( ln(h/2r_w)-\pi/2 \right )}

The effect of choke skin does not change the behavior of JD vs. n type curve, but the value of JD is multiplied by a factor that is a function of the number of fractures.

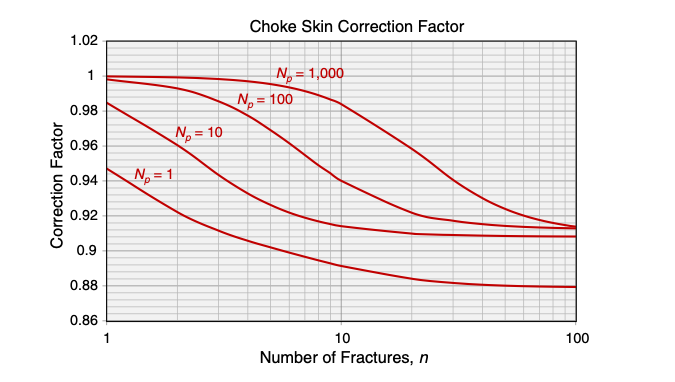
The correction factor as a function of n for xe/h = 65 and h/rw=250 ^[1].

The choke skin effect increases with the number of fractures, however this dependence finally flattens out ^[1].

Minimum fracture width constraint

To maintain fracture permeability k_f, at least three proppant grains of width are required.

To account for this practical requirement, the deviation from the technical optimum will be required^[2]. Instead of further decreasing the fracture width, the only possible option for a further increase in the number of fractures will be to decrease each fracture half-length. This will result in suboptimal performance of each fracture and, hence, suboptimal performance of the whole system in comparison to the ideal case without the minimum practical fracture width.

$Minimum fracture width constraint$
Effect of applying minimum fracture width constraint to the type curves (k=0.01md, kf=100d, xe=1609m, wmin=2.1mm) ^[1].

The J_D is no longer asymptotes to the technical maximum. Instead, the J_D decreases sharply as the number of fractures increases, because the fracture length is reduced to maintain minimum width.

For a given volume of proppant, with an increasing number of fractures, there is an ever- reducing volume per fracture. With less proppant per fracture, at some point, adding more fractures is detrimental to the overall well potential.

Flow Diagram

Workflow

Case Study

Main features

Plot of J_D as a function of n and N_p as parameter.
Plot of J_D as a function of N_p showing the width constraint influence.
Plot of J_D and w_f as a function of n for the given N_p .
Plot of J_D as a function of C_fD for the given n.
Design optimization curves which corresponds to the maximum J_D values for different N_p and n.
Optimum number of fractures n and well J_D.
Practical constrains envelope – minimum fracture width and choke skin effect.
Sensitivity for the different from the optimal n, X_f, I_x, C_fD, w_f.
Hydraulic fracturing proppant catalog with the predefined proppant properties.

Interface features

Save and share models with colleagues
Last saved model on current computer and browser is automatically opened
Metric and US oilfield units
Save as image and print plots by means of chart context menu (button at the upper-right corner of chart)
Download pdf report with input parameters, calculated values and plots
Select and copy results to Excel or other applications

References

↑ ^1.0 ^1.1 ^1.2 ^1.3 ^1.4 ^1.5 ^1.6 Guk, Vyacheslav; Tuzovskiy, Mikhail; Wolcott, Don; Mach, Joe (June 2019). "Optimizing Number of Fractures in Horizontal Well". SPE Journal. Society of Petroleum Engineers. 24 (SPE-174772-PA).
↑ Economides, Michael J.; Oligney, Ronald; Valko, Peter (2002). Unified Fracture Design: Bridging the Gap Between Theory and Practice. Alvin, Texas: Orsa Press.

Pages in category "OptiFracMS"

The following 7 pages are in this category, out of 7 total.

4

4/π stimulated well potential

6

6/π stimulated well potential

H

J

JD

O

OptiFracMS

[optifracMS-1] 1.0 ^1.1 ^1.2 ^1.3 ^1.4 ^1.5 ^1.6 Guk, Vyacheslav; Tuzovskiy, Mikhail; Wolcott, Don; Mach, Joe (June 2019). "Optimizing Number of Fractures in Horizontal Well". SPE Journal. Society of Petroleum Engineers. 24 (SPE-174772-PA).

[UFD2002-2] Economides, Michael J.; Oligney, Ronald; Valko, Peter (2002). Unified Fracture Design: Bridging the Gap Between Theory and Practice. Alvin, Texas: Orsa Press.

[1]

[2]

@@ Line 77: / Line 77: @@
 [[File:Minimum fracture width constraint.png | Minimum fracture width constraint]] <BR/>
 Effect of applying minimum fracture width constraint to the type curves (k=0.01md, kf=100d, xe=1609m, wmin=2.1mm) <ref name= optifracMS/>.
+The '''J<sub>D</sub>''' is no longer asymptotes to the technical maximum. Instead, the '''J<sub>D</sub>''' decreases sharply as the number of fractures increases, because the fracture length is reduced to maintain minimum width.
+For a given volume of proppant, with an increasing number of fractures, there is an ever- reducing volume per fracture. With less proppant per fracture, at some point, adding more fractures is detrimental to the overall well potential.
 == Flow Diagram ==

Navigation menu

Navigation

Categories

Products