Difference between revisions of "Category: OptiFrac"

Revision as of 13:55, 14 August 2018

Brief

pengtools optiFrac

optiFrac is a single well fracture design optimization tool.

For the given set of reservoir and proppant properties optiFrac calculates maximum achievable well productivity index (JD) and required fracture geometry.

In production optimization of hydraulic fracturing, it is important to recognize that for a fixed proppant volume, fracture length and fracture width compete to each other. Consequently, there is an optimum fracture length and width that would maximize the dimensionless productivity index of the fractured well ^[1]. Unified Fracture Design provides a methodology whereby for any given proppant volume the best combination of width and length could be determined ^[2].

optiFrac is available online at www.pengtools.com and in AppStore for iPad.

Typical applications

Optimization of hydraulic fracturing with Unified Fracture Design^[2]
Understanding post-fracturing production performance
Design Sensitivity Studies and Benchmarking
Optimum fracture design parameters determination:
- Dimensionless productivity index, J_D .
- Dimensionless Fracture conductivity, C_fD .
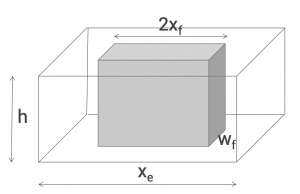
- Fracture half length, X_f .
- Fracture width, w .
- Fracture penetration, I_x .

Main features

Plot of J_D as a function of C_fD and I_x as parameter.
Plot of J_D as a function of C_fD and N_p as parameter.
Design optimization curve which corresponds to the maximum J_D values for different N_p.
Design Optimum Point at which the dimensionless productivity index, J_D, is maximized for the given proppant, fracture and reservoir parameters.
Physical constraints envelope.
Proppant library with predefined proppant properties.
Users Data Worksheet for benchmarking vs actual.

Interface features

Save and share models with colleagues
Last saved model on current computer and browser is automatically opened
Metric and US oilfield units
Save as image and print plots by means of chart context menu (button at the upper-right corner of chart)
Download pdf report with input parameters, calculated values and plots
Select and copy results to Excel or other applications

Math & Physics

Fracture Notation

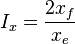I_x=\frac{2x_f}{x_e}

- penetration ratio ^[2],

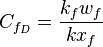C_{f_D}=\frac{k_f w_f}{k x_f}

- dimensionless fracture conductivity ^[2],

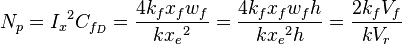N_p={I_x}^2 C_{f_D} = \frac{4 k_f x_f w_f}{k {x_e}^2} = \frac{4 k_f x_f w_f h}{k {x_e}^2 h} = \frac{2 k_f V_f}{k V_r}

- proppant numer ^[2],

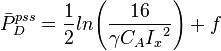{\bar{P}_D}^{pss} = \frac{1}{2} ln{\left (\frac{16}{\gamma C_A {I_x}^2} \right )} + f

- pseudo-steady state equation for finite-conductivity fractured wells ^[1],

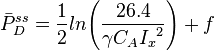{\bar{P}_D}^{ss} = \frac{1}{2} ln{\left (\frac{26.4}{\gamma C_A {I_x}^2} \right )} + f

- steady state equation for finite-conductivity fractured wells ^[1],

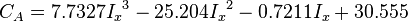C_{A}=7.7327 {I_x}^3 - 25.204 {I_x}^2 - 0.7211 I_x + 30.555

- shape factor ^[1].

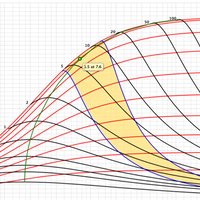
Type Curves

For finite fracture conductivities, the shape factors, C_A, can be calculated if the P_D is known for a specific value of I_x The P_D value could be obtained either by analytical solution or numerical simulations. After knowing C_A (which would be a function of I_x), “f-function” values can be calculated if PˆWD is known for a specific dimensionless fracture conductivity C_fD and fracture penetration I_x.

Type Curves were obtained, through seven hundred runs with a numerical simulator, modeling a fractured well in a closed square reservoir.

shows the dimensionless productivity index at pseudo-steady state as function of CfD, using IX as parameter and overlapping with the type curve with NP as parameter.

Workflow

Discussion

References

↑ ^1.0 ^1.1 ^1.2 ^1.3 Rueda, J.I.; Mach, J.; Wolcott, D. (2004). "Pushing Fracturing Limits to Maximize Producibility in Turbidite Formations in Russia" (SPE-91760-MS). Society of Petroleum Engineers.
↑ ^2.0 ^2.1 ^2.2 ^2.3 ^2.4 Economides, Michael J.; Oligney, Ronald; Valko, Peter (2002). Unified Fracture Design: Bridging the Gap Between Theory and Practice. Alvin, Texas: Orsa Press.

Pages in category "OptiFrac"

The following 6 pages are in this category, out of 6 total.

4

4/π stimulated well potential

6

6/π stimulated well potential

H

J

JD

O

OptiFrac

[pushing-1] 1.0 ^1.1 ^1.2 ^1.3 Rueda, J.I.; Mach, J.; Wolcott, D. (2004). "Pushing Fracturing Limits to Maximize Producibility in Turbidite Formations in Russia" (SPE-91760-MS). Society of Petroleum Engineers.

[UFD2002-2] 2.0 ^2.1 ^2.2 ^2.3 ^2.4 Economides, Michael J.; Oligney, Ronald; Valko, Peter (2002). Unified Fracture Design: Bridging the Gap Between Theory and Practice. Alvin, Texas: Orsa Press.

[1]

[2]

@@ Line 59: / Line 59: @@
 ==Type Curves==
+For finite fracture conductivities, the shape factors, '''C<sub>A</sub>''', can be calculated if the '''P<sub>D</sub>''' is known for a specific value of '''I<sub>x</sub>'''
+The '''P<sub>D</sub>''' value could be obtained either by analytical solution or numerical simulations. After knowing ''C<sub>A</sub>''' (which would be a function of  '''I<sub>x</sub>'''), “f-function” values can be calculated if PˆWD is known for a specific dimensionless fracture conductivity ''C<sub>fD</sub>''' and fracture penetration  '''I<sub>x</sub>'''.
+Type Curves were obtained, through seven hundred runs with a numerical simulator, modeling a fractured well in a closed square reservoir.
 shows the dimensionless productivity index at pseudo-steady state as function of CfD, using IX as parameter and overlapping with the type curve with NP as parameter.

Navigation menu

Navigation

Categories

Products