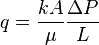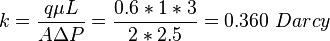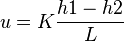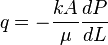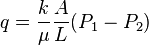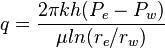Difference between revisions of "Darcy's law"

From wiki.pengtools.com
Jump to: navigation, search
(→‎Darcy's law)
(→‎See Also)
 
(24 intermediate revisions by the same user not shown)
Line 12: Line 12:
 
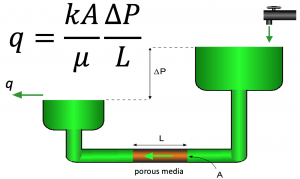
:<math>q=\frac{kA}{\mu} \frac{\Delta P}{L}</math>
 
:<math>q=\frac{kA}{\mu} \frac{\Delta P}{L}</math>
  
−
== Darcy's law History ==
+
where
 +
 
 +
:<math> A </math> = cross-sectional area, cm<sup>2</sup>
 +
:<math> k</math> = permeability, Darcy
 +
:<math> L </math> = length, cm
 +
:<math> P </math> = pressure, atm
 +
:<math> q </math> = flow rate, cm<sup>3</sup>/sec
 +
:<math> \mu </math> = fluid viscosity, cp
 +
 
 +
The permeability of 1 Darcy defined as permeability which allows fluid with viscosity of 1 centipoise flow a distance of 1 cm with velocity of 1 cc/sec through the crossectional area of 1 cm2 with the pressure gradient of 1 atm.
 +
 
 +
==Example==
 +
Determine the water phase permeability given the core lab test data:
 +
100% water saturation, A=2.5 cm2, L=3 cm, qw=0.6 cm3/sec, dP=2 atm, water viscosity 1 cP.
 +
 
 +
:<math>k=\frac{q \mu L}{A \Delta P} = \frac{0.6 *1 *3}{2*2.5}=0.360\ Darcy</math>
 +
 
 +
==History ==
 
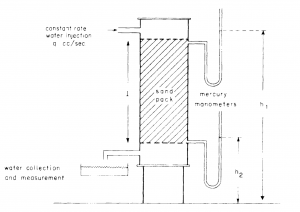
[[File:Darcy's experimental equipment.png|thumb|right|300px| Darcy's experimental equipment]]
 
[[File:Darcy's experimental equipment.png|thumb|right|300px| Darcy's experimental equipment]]
  
Line 21: Line 38:
 
:<math>u=K\frac{h1-h2}{L}</math>
 
:<math>u=K\frac{h1-h2}{L}</math>
  
−
All the experiments were carried out with water changing the type of sand pack. The effects of fluid density and viscosity on the flow was not investigated<ref name=DakeF/>.  
+
All the experiments were carried out with water changing the type of sand pack. The effects of fluid density and viscosity on the flow was not investigated<ref name=DakeF/> and therefore accounted for in the constant '''K'''.  
  
 
Subsequently, others experiments performed with a variety of different liquids revealed the dependence of fluid flow on fluid density and viscosity.  
 
Subsequently, others experiments performed with a variety of different liquids revealed the dependence of fluid flow on fluid density and viscosity.  
Line 27: Line 44:
 
The new constant '''k''' has therefore been isolated as being solely dependent on the nature of sand and is described as the '''permeability'''<ref name=DakeF/>.
 
The new constant '''k''' has therefore been isolated as being solely dependent on the nature of sand and is described as the '''permeability'''<ref name=DakeF/>.
  
−
== Darcy's law equation ==
+
== Equation ==
 
===Differential form ===
 
===Differential form ===
 
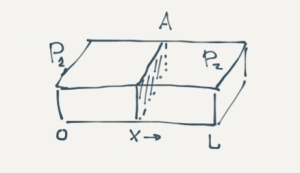
If distance is measured positive in the direction of flow, then the pressure gradient must be negative in the same direction since fluids move from high to low pressure<ref name=DakeF/>. Therefore, Darcy's law is:
 
If distance is measured positive in the direction of flow, then the pressure gradient must be negative in the same direction since fluids move from high to low pressure<ref name=DakeF/>. Therefore, Darcy's law is:
Line 44: Line 61:
 
*Constant fluid compressibility
 
*Constant fluid compressibility
 
*Constant temperature
 
*Constant temperature
−
 
−
==Darcy's law equation example==
 
−
The permeability of 1 Darcy defined as permeability which allows fluid with viscosity of 1 centipoise flow with velocity of 1 cc/sec through the crossectional area of 1 cm2 with the pressure gradient of 1 atm.
 
  
 
== Inflow Equations Derivation ==
 
== Inflow Equations Derivation ==
Line 52: Line 66:
 
Derivation of the Linear and Radial Inflow Equations
 
Derivation of the Linear and Radial Inflow Equations
 
[[File:Darcy's Law mtuz.png|800px]]
 
[[File:Darcy's Law mtuz.png|800px]]
−
 
−
== Nomenclature  ==
 
−
 
−
:<math> A </math> = cross-sectional area, cm<sup>2</sup>
 
−
:<math> k</math> = permeability, d
 
−
:<math> L </math> = length, cm
 
−
:<math> P </math> = pressure, atm
 
−
:<math> q </math> = flow rate, cm<sup>3</sup>/sec
 
−
 
−
===Greek symbols===
 
−
 
−
:<math> \mu </math> = [[Darcy's law]] fluid viscosity, cp
 
  
 
==See Also==
 
==See Also==
  
−
* Converting from the Darcy's law units to the field units in the well's inflow equations [[141.2 derivation]]
+
* [[141.2 derivation]] Converting from the Darcy's law units to the field units in the well's inflow equations
 +
* [[18.41 derivation]] Converting from the Darcy's law units to the metric units in the well's inflow equations
 
* Calculating [[Production Potential]] with the [[Darcy's law]]
 
* Calculating [[Production Potential]] with the [[Darcy's law]]
 +
* [[Petroleum Engineering]]
 +
* [[Relative Permeability]]
 +
* [[JD]]
 +
* [[Productivity index|J]]
  
 
==References==
 
==References==
Line 106: Line 113:
 
[[Category:E&P Portal]]
 
[[Category:E&P Portal]]
 
[[Category:pengtools]]
 
[[Category:pengtools]]
 +
[[Category:Mature Water Flood Analysis]]
  
 
{{#seo:
 
{{#seo:
−
|title=Darcy's law | Equation Formula Examples
+
|title=Darcy's law | Equation Formula Examples | Petroleum Engineering
 
|titlemode= replace
 
|titlemode= replace
 
|keywords=Darcy's law equation
 
|keywords=Darcy's law equation
−
|description=Darcy's law equation and derivation.
+
|description=Darcy's law equation, history, examples, derivation and applications in petroleum engineering.
 
}}
 
}}

Latest revision as of 13:43, 9 July 2023

Darcy's law

Darcy's law. Equation and notations

Darcy's law is the fundamental law of fluid motion in porous media published by Henry Darcy in 1856 [1]. French engineer Henry Darcy has earned himself a special place in history as the first experimental reservoir engineer [2].

Darcy's law has been successfully applied to determine the flow through permeable media since the early days of Petroleum Engineering.

The basic form of Darcy's law is very similar to in form to other physical laws. For example Fourier's law for heat conduction and Ohm's law for flow of electricity [3].

Darcy's law formula:

q=\frac{kA}{\mu} \frac{\Delta P}{L}

where

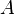A = cross-sectional area, cm2
k = permeability, Darcy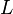
L = length, cm
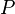P = pressure, atm
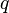q = flow rate, cm3/sec
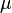\mu = fluid viscosity, cp

The permeability of 1 Darcy defined as permeability which allows fluid with viscosity of 1 centipoise flow a distance of 1 cm with velocity of 1 cc/sec through the crossectional area of 1 cm2 with the pressure gradient of 1 atm.

Example

Determine the water phase permeability given the core lab test data: 100% water saturation, A=2.5 cm2, L=3 cm, qw=0.6 cm3/sec, dP=2 atm, water viscosity 1 cP.

k=\frac{q \mu L}{A \Delta P} = \frac{0.6 *1 *3}{2*2.5}=0.360\ Darcy

History

Darcy's experimental equipment

Henry Darcy worked on the design of a filter large enough to process the Dijon towns daily water requirement [2].

By flowing water through the sand pack Darcy established that, for any flow rate, the velocity of the flow was directly proportional to the difference in manometric heights[2]:

u=K\frac{h1-h2}{L}

All the experiments were carried out with water changing the type of sand pack. The effects of fluid density and viscosity on the flow was not investigated[2] and therefore accounted for in the constant K.

Subsequently, others experiments performed with a variety of different liquids revealed the dependence of fluid flow on fluid density and viscosity.

The new constant k has therefore been isolated as being solely dependent on the nature of sand and is described as the permeability[2].

Equation

Differential form

If distance is measured positive in the direction of flow, then the pressure gradient must be negative in the same direction since fluids move from high to low pressure[2]. Therefore, Darcy's law is:

q = -\frac{kA}{\mu} \frac{dP}{dL}

Linear form

q = \frac{k}{\mu} \frac{A}{L} (P_1 - P_2) Darcy's Law Linear form equation notation

Radial form

q = \frac{2 \pi kh (P_e - P_w)}{\mu ln(r_e/r_w)} Darcy's Law Radial form equation notation

Conditions

  • Single fluid
  • Steady stay flow
  • Constant fluid compressibility
  • Constant temperature

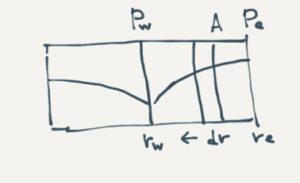
Inflow Equations Derivation

Derivation of the Linear and Radial Inflow Equations Darcy's Law mtuz.png

See Also

References

  1. ↑ Darcy, Henry (1856). "Les Fontaines Publiques de la Ville de Dijon". Paris: Victor Dalmont. 
  2. ↑ 2.0 2.1 2.2 2.3 2.4 2.5 Dake, L.P. (1978). Fundamentals of Reservoir Engineering. Amsterdam, Hetherlands: Elsevier Science. 
  3. ↑ Wolcott, Don (2009). Applied Waterflood Field DevelopmentPaid subscription required. Houston: Energy Tribune Publishing Inc. 
Retrieved from "https://wiki.pengtools.com/index.php?title=Darcy%27s_law&oldid=7663"