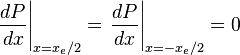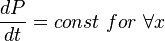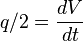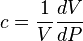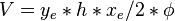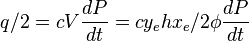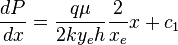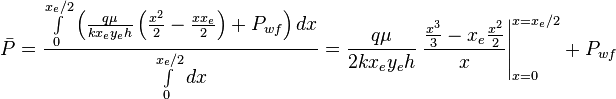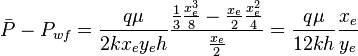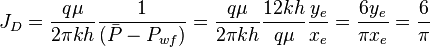Difference between revisions of "6/π stimulated well potential"

From wiki.pengtools.com
Jump to: navigation, search
(→‎Math & Physics)
(→‎Brief)
 
(3 intermediate revisions by the same user not shown)
Line 2: Line 2:
 
[[File:fracture linear flow.png|thumb|right|300px| Stimulated well drainage]]
 
[[File:fracture linear flow.png|thumb|right|300px| Stimulated well drainage]]
  
−
[[6/π stimulated well potential |6/π]] is the maximum possible stimulation potential for pseudo steady state linear flow in a square well spacing.
+
[[6/π stimulated well potential |6/π]] is the maximum possible stimulation well potential for pseudo steady state linear flow in a square well spacing.
  
 
==Math & Physics==
 
==Math & Physics==
Line 53: Line 53:
  
 
==See also==
 
==See also==
 +
[[4/π stimulated well potential]]<BR/>
 
[[JD]]<BR/>
 
[[JD]]<BR/>
 
[[:Category:optiFrac | optiFrac]]<BR/>
 
[[:Category:optiFrac | optiFrac]]<BR/>
Line 81: Line 82:
  
  
 +
[[Category:pengtools]]
 
[[Category:Technology]]
 
[[Category:Technology]]
 
[[Category:optiFrac]]
 
[[Category:optiFrac]]
 
[[Category:optiFracMS]]
 
[[Category:optiFracMS]]
 
[[Category:fracDesign]]
 
[[Category:fracDesign]]
 +
 +
{{#seo:
 +
|title=Hydraulic fracturing formulas 6/π
 +
|titlemode= replace
 +
|keywords=hydraulic fracturing, hydraulic fracturing formulas, well potential
 +
|description=Hydraulic fracturing formulas maximum possible stimulation well potential for pseudo steady state linear flow 6/π
 +
}}

Latest revision as of 06:40, 10 December 2018

Brief

Stimulated well drainage

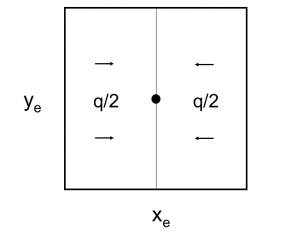
6/π is the maximum possible stimulation well potential for pseudo steady state linear flow in a square well spacing.

Math & Physics

Pseudo steady state flow boundary conditions:

\left. \frac{dP}{dx} \right|_{x=x_e/2} = \left. \frac{dP}{dx} \right|_{x=-x_e/2} = 0
\frac{dP}{dt} =const\ for \ \forall x

From Diffusivity Equation:

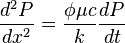\frac{d^2P}{dx^2}=\frac{\phi \mu c}{k} \frac{dP}{dt} ( 1 )

From Material Balance:

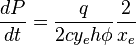q/2 =\frac{dV}{dt}
c=\frac{1}{V} \frac{dV}{dP}
V =y_e*h*x_e/2*\phi
q/2 =c V\frac{dP}{dt} = c y_e h x_e/2 \phi \frac{dP}{dt}
\frac{dP}{dt} = \frac{q}{2 c y_e h \phi} \frac{2}{x_e} ( 2 )

( 2 ) - > ( 1 ) :

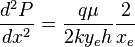\frac{d^2P}{dx^2}=\frac{q \mu}{2 k y_e h} \frac{2}{x_e} ( 3 )

Integrating ( 3 ):

\frac{dP}{dx}=\frac{q \mu}{2 k y_e h} \frac{2}{x_e} x + c_1
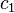c_1 must satisfy boundary condition: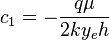 c_1 = - \frac{q \mu}{2 k y_e h}
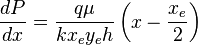\frac{dP}{dx}=\frac{q \mu}{k x_e y_e h} \left ( x- \frac{x_e}{2} \right ) ( 4 )

Integrating ( 4 ):

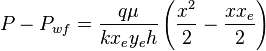P - P_{wf} = \frac{q \mu}{k x_e y_e h} \left ( \frac{x^2}{2} - \frac{x x_e}{2} \right ) ( 5 )

Since average pressure is: 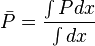\bar P = \frac{\int P dx}{\int dx}:

\bar P = \frac{ \int \limits_{0}^{x_e/2} \left ( \frac{q \mu}{k x_e y_e h} \left ( \frac{x^2}{2} - \frac{x x_e}{2} \right ) + P_{wf} \right ) dx}{\int \limits_{0}^{x_e/2}dx} = \frac{q \mu}{2 k x_e y_e h} \left. \frac{\frac{x^3}{3} - x_e \frac{x^2}{2}}{x} \right|_{x=0}^{x=x_e/2} + P_{wf}
\bar P - P_{wf} = \frac{q \mu}{2 k x_e y_e h} \frac{\frac{1}{3} \frac{x_e^3}{8} -\frac{x_e}{2} \frac{x_e^2}{4}}{\frac{x_e}{2}} = \frac{q \mu}{12 k h} \frac{x_e}{y_e}
J_D=\frac{q \mu}{2 \pi k h} \frac{1}{( \bar P - P_{wf})} =\frac{q \mu}{2 \pi k h} \frac{12 k h}{q \mu} \frac{y_e}{x_e} = \frac{6 y_e}{\pi x_e}=\frac{6}{\pi}

See also

4/π stimulated well potential
JD
optiFrac
fracDesign
Production Potential

Nomenclature

A = cross-sectional area, cm2
c = total compressibility, atm-1
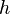h = thickness, m
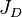J_D = dimensionless productivity index, dimensionless
k = permeability, d
P = pressure, atm
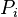P_i = initial pressure, atm
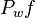P_wf = well flowing pressure, atm
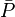\bar P = average pressure, atm
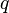q = flow rate, cm3/sec
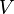V = one wing volume, m3
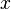x = length, m
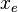x_e = drinage area length, m
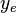y_e = drinage area width, m

Greek symbols

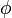\phi = porosity, fraction
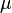\mu =viscosity, cp
Retrieved from "https://wiki.pengtools.com/index.php?title=6/π_stimulated_well_potential&oldid=5595"