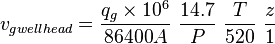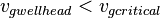Liquid loading
Contents
Brief
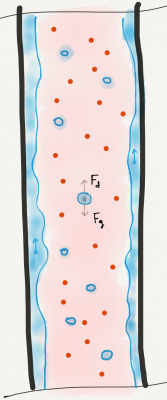
Liquid loading is a phenomenon when the gas phase does't provide sufficient transport energy to lift the liquids out of the well.
In 1969 Turner et al. published an empirical correlation defining the Liquid loading gas velocity[1].
Math & Physics
The minimum gas velocity to remove the liquid equation:
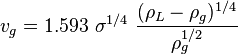 [2] (1)
[2] (1)
Note that original paper[1] uses 20.4 constant which is good if the surface tension units are in 'lbf/ft'. Also 20.4 is calculated by adjusting the theoretical equation constant by 20 percent. For the reference PROSPER uses 2.04. PQplot uses 1.593.
The minimum gas rate to remove the liquid equation:
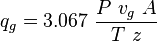 (2)
(2)
PQplot workflow
In order to calculate the liquid loading point in PQplot:
For every point in the VLP curve:
1. Critical gas velocity at the wellhead is calculated by eq (1)
2. Wellhead flowing gas velocity is calculated
3. Liquid loading flag is 1 if:
4. Critical gas rate is the last VLP curve point at which liquid loading flag is 1.
Discussion
To avoid the Liquid loading the gas velocity should be above the Liquid loading velocity.
The higher the gas rate the higher the gas velocity.
The lower the wellhead flowing pressure the higher the gas rate.
The bigger the tubing ID the higher the gas rate.
In case when the gas rate is limited by the Reservoir deliverability smaller tubing ID will increase the gas velocity.
Example. Calculating critical gas velocity and rate
Example 3-2 from [2]
Input data
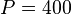 , flowing wellhead pressure, psia
, flowing wellhead pressure, psia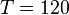 , flowing wellhead temperature, °F
, flowing wellhead temperature, °F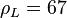 , liquid density, lbm/ft3
, liquid density, lbm/ft3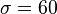 , water surface tension, dyne/cm
, water surface tension, dyne/cm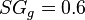 , gas specific gravity
, gas specific gravity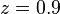 , gas compressibility factor
, gas compressibility factor
Production string = 2-3/8 inch tubing with 1.995 in ID, A = .0217 ft2
Water is the produced liquid
Solution
Calculate the gas density:
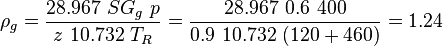 , lbm/ft2
, lbm/ft2
Calculate the critical gas velocity form (1):
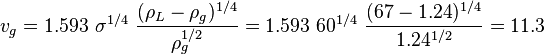 , ft/sec
, ft/sec
Calculate the critical gas rate form (2):
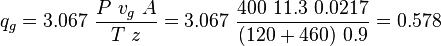 , MMscfd
, MMscfd
Solution with PQplot
PQplot calculates the following critical gas rate:
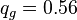 , MMscfd
, MMscfd
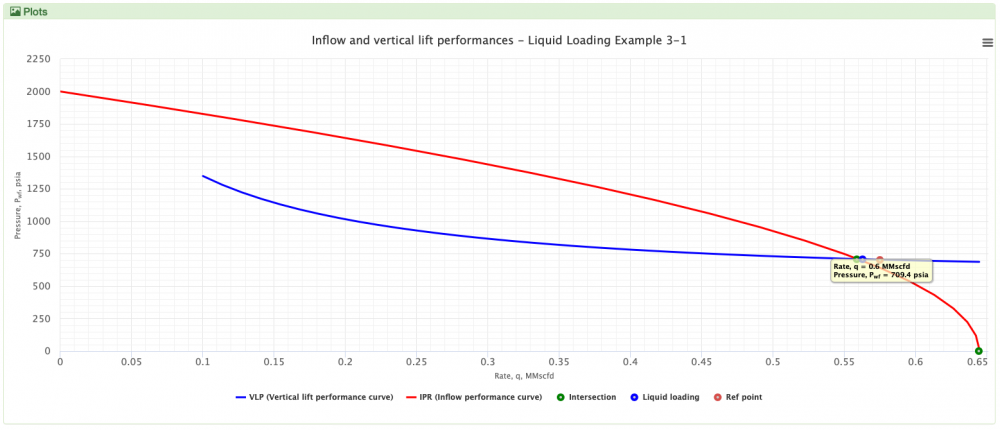
Liquid loading example 3-1 (Public model)
Nomenclature
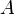 = flow area, ft^2
= flow area, ft^2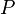 = flowing wellhead pressure, psia
= flowing wellhead pressure, psia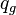 = gas rate, MMscf/d
= gas rate, MMscf/d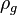 = gas density, lbm/ft3
= gas density, lbm/ft3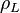 = liquid density, lbm/ft3
= liquid density, lbm/ft3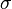 = surface tension, dyne/cm (ref values: 60 - water, 20 - condensate) [1]
= surface tension, dyne/cm (ref values: 60 - water, 20 - condensate) [1]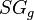 = gas specific gravity
= gas specific gravity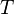 = flowing wellhead temperature, °R
= flowing wellhead temperature, °R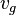 = gas velocity, ft/sec
= gas velocity, ft/sec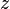 = gas compressibility factor at flowing P & T, dimensionless
= gas compressibility factor at flowing P & T, dimensionless
See also
References
- ↑ 1.0 1.1 1.2 Turner, R. G.; Hubbard, A. E.; Dukler (Nov 1969). "Analysis and Prediction of Minimum Flow Rate for the Continuous Removal of Liquids from Gas Wells"
 . Journal of Petroleum Technology (SPE-2198-PA): 1475–1482.
. Journal of Petroleum Technology (SPE-2198-PA): 1475–1482.
- ↑ 2.0 2.1 Lea, J. F.; Nickens, M.; Wells (2011). Gas Well Deliquification
 . Energy Tribune Publishing Inc.
. Energy Tribune Publishing Inc.