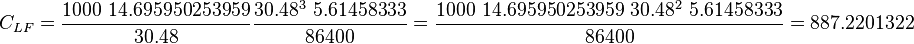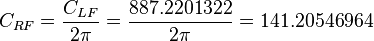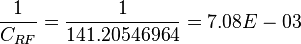141.2 derivation
From wiki.pengtools.com
Brief
141.2 is the well know constant which is used for converting from the Darcy's law units to the field units in the well's inflow equations.
For example Darcy's law for the single-phase flow is as follows[1]:
The derivation of the 141.2 constant is given below.
Math and Physics
In Darcy's units:
Converting to the field units:
So:
And:
where
For the radial flow:
One can be familiar with the inverse of the 141.2 constant:
See Also
Nomenclature
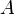 = Darcy's law cross-sectional area, cm2
= Darcy's law cross-sectional area, cm2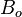 = oil formation volume factor, bbl/stb
= oil formation volume factor, bbl/stb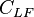 = linear flow units conversion constant
= linear flow units conversion constant 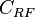 = radial flow units conversion constant
= radial flow units conversion constant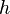 = effective feet of oil pay, ft
= effective feet of oil pay, ft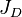 = dimensionless productivity index, dimensionless
= dimensionless productivity index, dimensionless = Darcy's law permeability, d
= Darcy's law permeability, d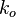 = effective permeability to oil, md
= effective permeability to oil, md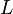 = Darcy's law length, cm
= Darcy's law length, cm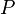 = Darcy's law pressure, atm
= Darcy's law pressure, atm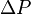 = drawdown, psia
= drawdown, psia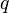 = Darcy's law flow rate, cm3/sec
= Darcy's law flow rate, cm3/sec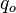 = oil flow rate, stb/d
= oil flow rate, stb/d
Greek symbols
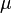 = Darcy's law oil viscosity, cp
= Darcy's law oil viscosity, cp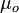 = oil viscosity, cp
= oil viscosity, cp
References
- ↑ Brown, Kermit (1984). The Technology of Artificial Lift Methods. Volume 4. Production Optimization of Oil and Gas Wells by Nodal System Analysis. 4. Tulsa, Oklahoma: PennWellBooks.
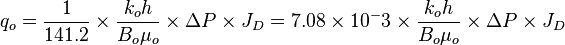
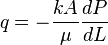
![\frac{[cm^3]}{[sec]} = - \frac{[D][cm^2]}{[cP]} \frac{[atm]}{[cm]}](/images/math/5/5/5/555b9dc7f65e6db7f1cd05153aaae770.png)
![\frac{[cm^3] \frac{[ft^3]}{[30.48^3 cm^3]} \frac{[bbl]}{[5.61458333 ft^3]} }{[sec] \frac{[day]}{[86400 sec]}} = - \frac{[D] \frac{[1000 mD]}{[D]}[cm^2] \frac{[ft^2]}{[30.48^2 cm^2]}}{[cP]} \frac{[atm] \frac{[14.695950253959 psia]}{[atm]}}{[cm] \frac{[ft]}{[30.48 cm]}}](/images/math/a/e/f/aef6ab96a93f70f9312ea71cca7aeb57.png)
![\frac{[bbl]}{[day]} \frac{86400}{30.48^3\ 5.61458333} = - \frac{[mD][ft^2]}{[cP]} \frac{[psia]}{[ft]} \frac{1000\ 14.695950253959}{30.48}](/images/math/9/a/b/9abe955d3e8338add13d1fe96e9fd738.png)
![\frac{[bbl]}{[day]} = - C_{LF} \frac{[mD][ft^2]}{[cP]} \frac{[psia]}{[ft]}](/images/math/d/d/4/dd4c5bbb71e5c38a6ae238f62d56d9ea.png)