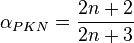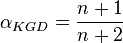Category: FracDesign

From wiki.pengtools.com
Revision as of 09:26, 12 October 2018 by MishaT (talk | contribs) (→‎Comparison study)
Jump to: navigation, search

Brief

pengtools fracDesign

fracDesign is a tool for designing a hydraulic fracture treatment in pengtools.

For the given set of reservoir, fluid and proppant properties fracDesign calculates the pumping schedule which will create the optimal fracture geometry to achieve maximum well’s productivity.

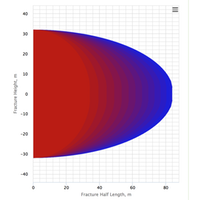
fracDesign algorithm is based on widely used fracture PKN and KGD models (see [1]. Pumping schedule realizes the optimal fracture geometry and assures uniform placement of the proppant (see [2]). If the optimum placement cannot be realized by traditional means, a TSO design option is available. Like any other model fracDesign inevitably uses a number of mathematical idealizations.

fracDesignis available online at www.pengtools.com.

Typical applications

  • Design mode: Calculating the pumping schedule required to achive optimal fracture geometry
  • Providing initial guess pumping schedule for more complex fracture simulators
  • Optimization of hydraulic fracture design with Unified Fracture Design[2]
  • Simulation mode: Simulation of the fracture geometry based on the given pumping schedule with PKN and KGD models
  • TSO design
  • Sensitivity studies: By modifying various input parameters, an intuitive feel for their relative importance in treatment design and final fractured well performance can be rapidly acquired

Math & Physics

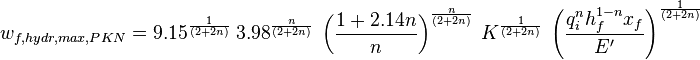w_{f,hydr,max,PKN}=9.15^{\frac{1}{(2 + 2 n)}}\ 3.98^{\frac{n}{(2 + 2 n)}}\ \left ( \frac{1+2.14n}{n}\right )^{\frac{n}{(2 + 2 n)}}\ K^{\frac{1}{(2 + 2 n)}}\ \left ( \frac{q_i^n h_f^{1-n} x_f}{E'} \right )^{\frac{1}{(2 + 2 n)}} - hydraulic maximum fracture width PKN (ref[1] eq 9.53)
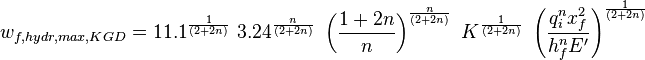w_{f,hydr,max,KGD}=11.1^{\frac{1}{(2 + 2 n)}}\ 3.24^{\frac{n}{(2 + 2 n)}}\ \left ( \frac{1+2n}{n}\right )^{\frac{n}{(2 + 2 n)}}\ K^{\frac{1}{(2 + 2 n)}}\ \left ( \frac{q_i^n x_f^2}{h_f^n E'} \right )^{\frac{1}{(2 + 2 n)}} - hydraulic maximum fracture width KGD (ref[1] eq 9.55)
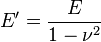E'=\frac{E}{1-\nu^2} - plain strain modulus
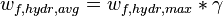w_{f,hydr,avg} = w_{f,hydr,max} * \gamma - hydraulic average fracture width
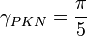\gamma_{PKN}=\frac{\pi}{5} - shape factor PKN (ref[1] eq 9.10)
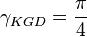\gamma_{KGD}=\frac{\pi}{4} - shape factor KGD (ref[1] eq 9.24)
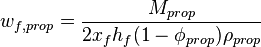w_{f,prop}=\frac{M_{prop}}{2 x_f h_f (1-\phi_{prop}) \rho_{prop}} - propped fracture width
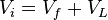V_i = V_f + V_L - mass balance equation (ref[1] eq 8.1)
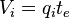V_i = q_i t_e - injected volume into one fracture wing
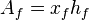A_f = x_f h_f - the area of one face of one wing for rectangular fracture shape
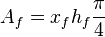A_f = x_f h_f \frac{\pi}{4} - the area of one face of one wing for elliptic fracture shape
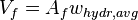V_f = A_f w_{hydr,avg} - volume of fluid contained in one fracture wing
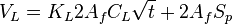V_L = K_L 2 A_f C_L \sqrt{t} + 2 A_f S_p - volume of fluid leak-off to formation through the two created fracture surfaces of one wing
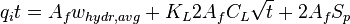q_i t = A_f w_{hydr,avg} + K_L 2 A_f C_L \sqrt{t} + 2 A_f S_p - mass balance equation (ref[2] eq 4.6)
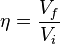\eta = \frac{V_f}{V_i} - fluid efficiency

Opening time distribution factor KL

Nolte opening time distribution factor KL

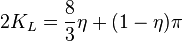2 K_L=\frac{8}{3} \eta + ( 1 - \eta) \pi - (ref[1] eq 8.36)

Carter opening time distribution factor KL

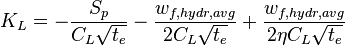K_L=-\frac{S_p}{C_L \sqrt{t_e}} - \frac{w_{f,hydr,avg}}{2C_L\sqrt{t_e}} + \frac{w_{f,hydr,avg}}{2 \eta C_L \sqrt{t_e}} (ref [2] eq 4.8)

where:

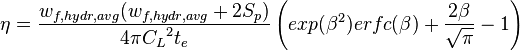\eta=\frac{w_{f,hydr,avg}(w_{f,hydr,avg}+2S_p)}{4\pi {C_L}^2 t_e} \left ( exp(\beta^2) erfc(\beta) + \frac{2\beta}{\sqrt\pi} - 1 \right )(ref [2] eq 4.9)

and:

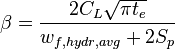\beta=\frac{2C_L \sqrt{\pi t_e}}{w_{f,hydr,avg} + 2S_p}(ref [2] eq 4.9)

Nolte G-function for opening time distribution factor KL

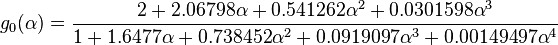g_0(\alpha)=\frac{2 + 2.06798 \alpha + 0.541262 \alpha^2 + 0.0301598 \alpha^3}{1 + 1.6477 \alpha + 0.738452 \alpha^2 + 0.0919097 \alpha^3 + 0.00149497 \alpha^4}(ref [2] eq 4.12)

where:

\alpha_{PKN} =\frac{2n+2}{2n+3}
\alpha_{KGD} =\frac{n+1}{n+2}

Pumping schedule

According to Nolte[3] the schedule is derived from the following assumptions:

  • the whole length created should be propped
  • at the end of pumping, the proppant distribution in the fracture should be uniform
  • the proppant schedule should be of the form of a delayed power law with the Nolte's exponent and the fraction of pad being equal
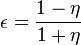\epsilon= \frac{1-\eta}{1+\eta} - Nolte exponent
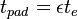t_{pad}=\epsilon t_e - pad pumping time
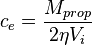c_e=\frac{M_{prop}}{2\eta V_i} - proppant concentration at the end of pumping
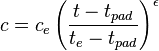c=c_e \left ( \frac{t-t_{pad}}{t_e-t_{pad}} \right )^{\epsilon} - slurry concentration vs time
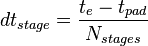dt_{stage}=\frac{t_e - t_{pad}}{N_{stages}} - ramping stage duration
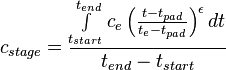c_{stage} = \frac {\int \limits_{t_{start}}^{t_{end}} c_e \left ( \frac{t-t_{pad}}{t_e-t_{pad}} \right )^{\epsilon} dt}{t_{end}-t_{start}} - ramping stage slurry concentration
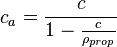c_a=\frac{c}{1-\frac{c}{\rho_{prop}}} - conversion form slurry concentration (proppant mass per unit of injected slurry) to clean concentration (proppant mass per unit of injected clean/base/"neat" fluid)

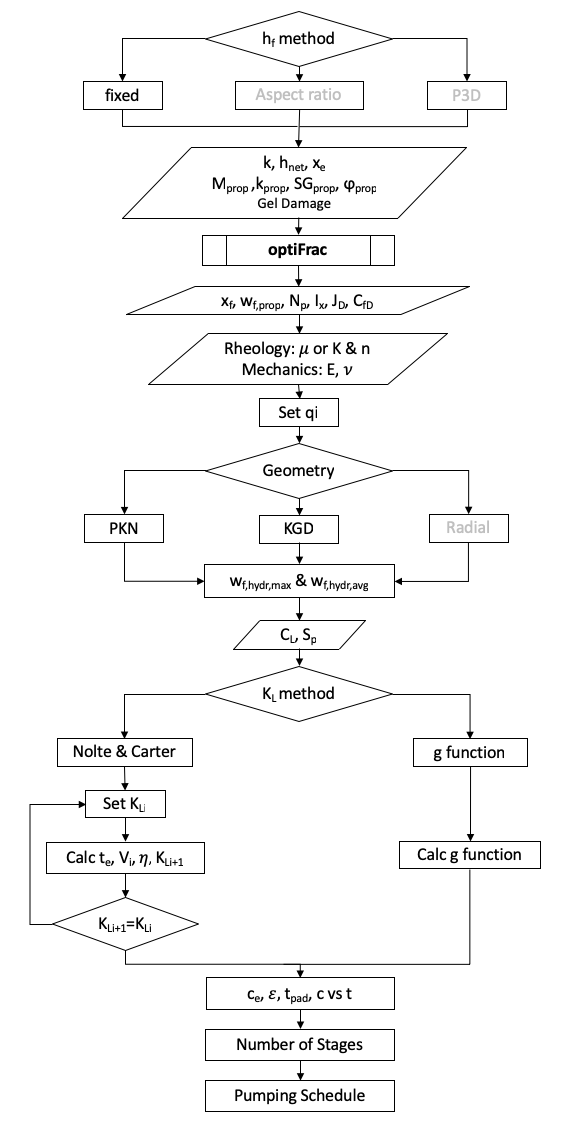
Flow Diagram

Design mode

FracDesign design mode flow diagram.png

Simulation mode

FracDesign simulation mode flow diagram.png

Workflow

Design mode

  1. Input the fracture height, hf
  2. Run optiFrac to get optimum xf and wf, prop
  3. Calculate maximum and average hydraulic fracture widths : wf,hydr,max and wf,hydr,avg
  4. Calculate opening time distribution factor, KL
  5. Solve mass balance equation for total pumping time, te
  6. Calculate fluid efficiency, η
  7. Calculate Nolte's exponent, ε
  8. Calculate pad time, tpad
  9. Calculate proppant concentration at the end of pumping, ce
  10. Calculate slurry concentration vs time curve, c vs t
  11. Set the number of stages, Nstage
  12. Calculate slurry concentration at each stage, cstage

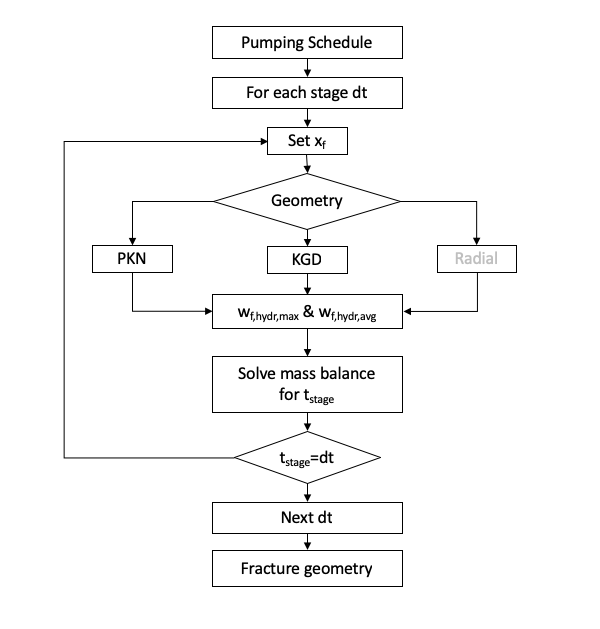
Simulation mode

  1. Input the fracture height, hf
  2. Input the pumping schedule, dt, cstage for each Nstage
  3. For each stage duration, dt
    1. Set the xf
    2. Calculate maximum and average hydraulic fracture widths : wf,hydr,max and wf,hydr,avg
    3. Calculate opening time distribution factor, KL
    4. Solve mass balance equation for total pumping time, tstage
    5. Iterate until tstage=dt
  4. Move to the next stage

Note that: Distribution of the proppant in the fracture is not modelled in the simulation mode. Only geometry evolution and byproducts are simulated under assumption that proppant is uniformly distributed in fracture.

TSO

Comparison study

Main features

  • PKN and KGD fracture geometry models
  • optiFrac workflow on fracture geometry optimization
  • Slurry concentration versus time pumping schedule as plot and table
  • Fracture length and width profiles vs time plots
  • Net pressure profiles vs time as plot and table
  • Practical pumping constrains and Fracture tuning options
  • Detailed output table with calculated fracture design parameters
  • Sensitivity option with benchmark to potential
  • Simulation mode: calculating the fracture geometry from the given pumping schedule
  • "New model" button resets input values to the default values.
  • Switch between Metric and Field units.
  • Save/load models to the files and to the user’s cloud.
  • Export pdf report containing input parameters, calculated values and the chart.
  • Share models to the public cloud or by using model’s link.
  • Continue your work from where you stopped: last saved model will be automatically opened.
  • Download the chart as an image or data and print (upper-right corner chart’s button).

Nomenclature

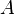A = surface area, m2
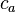c_a = clean concentration (proppant mass per unit of injected clean/base/"neat" fluid), kg/m3
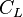C_L = leak-off coefficient, m/s0.5
c = slurry concentration (proppant mass per unit of injected slurry), kg/m3
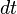dt = time step, sec
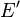E' = plain strain modulus, Pa
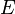E = Young's Modulus, Pa
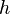h = height, m
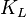K_L = opening time distribution factor, dimensionless
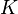K = rheology consistency index, Pa*sn
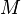M = mass, kg
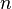n = rheology flow behavior index, dimensionless
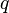q = slurry injection rate for one wing, m3/sec
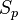S_p = spurt loss coefficient, m
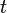t = pumping time, sec
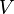V = volume, m3
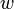w = width, m
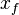x_f = fracture half-length, m

Greek symbols

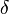\delta = dry to wet width ratio at the end of pumping, usually 0.5-0.7
\epsilon = Nolte exponent, dimensionless
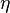\eta = fluid efficiency, fraction
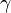\gamma = geometric factor in vertical direction, dimensionless
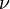\nu = Poisson's ratio, dimensionless
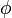\phi = porosity, fraction
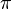\pi = 3.1415
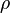\rho = density, kg/m3

Subscripts

avg = average
e = end of pumping
f = fracture
gross = gross
hydr = hydraulic
i = injected
KGD = Khristianovic-Geertsma-de Klerk geometry
L = leak-off
max = maximum
net = net
pad = pad
PKN = Perkins-Kern-Nordgren geometry
prop = propped or proppant
r = reservoir

References

  1. ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 Valko, Peter; Economides, Michael J. (1995). Hydraulic fracture mechanics. Texas A & M University: John Wiley and Sons. 
  2. ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 Economides, Michael J.; Oligney, Ronald; Valko, Peter (2002). Unified Fracture Design: Bridging the Gap Between Theory and Practice. Alvin, Texas: Orsa Press. 
  3. ↑ Nolte, K.G. (1986). "Determination of Proppant and Fluid Schedules From Fracturing-Pressure Decline"Free registration required (SPE-13278-PA). Society of Petroleum Engineers. 
Retrieved from "https://wiki.pengtools.com/index.php?title=Category:FracDesign&oldid=5044"