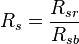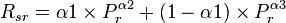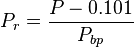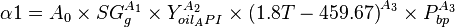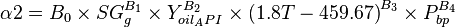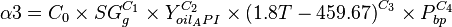Difference between revisions of "Velarde solution gas oil ratio correlation"
From wiki.pengtools.com
| Line 20: | Line 20: | ||
A4 = 1.056052<br/> | A4 = 1.056052<br/> | ||
| − | :<math> \alpha1 = A_0 \times SG^{A_1}_g \times Y^{A_2}_{oil_API} \times {(T- 459.67)}^{A_3} \times P^{A_3}_{bp} </math> | + | :<math> \alpha1 = A_0 \times SG^{A_1}_g \times Y^{A_2}_{oil_API} \times {(1.8 T- 459.67)}^{A_3} \times P^{A_3}_{bp} </math> |
B0 = 0.1004<br/> | B0 = 0.1004<br/> | ||
| Line 28: | Line 28: | ||
B4 = 0.302065<br/> | B4 = 0.302065<br/> | ||
| − | :<math>\alpha2 = B_0 \times SG^{B_1}_g \times Y^{B_2}_{oil_API} \times {(T - 459.67)}^{B_3} \times P^{B_4}_{bp}</math> | + | :<math>\alpha2 = B_0 \times SG^{B_1}_g \times Y^{B_2}_{oil_API} \times {(1.8 T - 459.67)}^{B_3} \times P^{B_4}_{bp}</math> |
C0 = 0.9167<br/> | C0 = 0.9167<br/> | ||
| Line 36: | Line 36: | ||
C4 = 0.047094<br/> | C4 = 0.047094<br/> | ||
| − | :<math>\alpha3 = C_0 \times SG^{C_1}_g \times Y^{C_2}_{oil_API} \times {(T - 459.67)}^{C_3} \times P^{C_4}_{bp}</math> | + | :<math>\alpha3 = C_0 \times SG^{C_1}_g \times Y^{C_2}_{oil_API} \times {(1.8 T - 459.67)}^{C_3} \times P^{C_4}_{bp}</math> |
=== Discussion === | === Discussion === | ||
Revision as of 08:25, 28 September 2020
Brief
Velarde correlation is an empirical correlation for the solution gas oil ratio published in 1997. [1]
Math & Physics
where:
A0 = 1.8653e-4
A1 = 1.672608
A2 = 0.929870
A3 = 0.247235
A4 = 1.056052
B0 = 0.1004
B1 = -1.00475
B2 = 0.337711
B3 = 0.132795
B4 = 0.302065
C0 = 0.9167
C1 = -1.48548
C2 = -0.164741
C3 = -0.09133
C4 = 0.047094
Discussion
Why the Velarde correlation?
Application range
Nomenclature
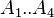= coefficients
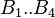= coefficients
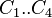= coefficients
= pressure, MPA
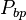= bubble point pressure, MPA
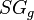= gas specific gravity, dimensionless
= temperature, °R
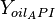= oil API gravity, dimensionless
References
- ↑ 1.0 1.1
Velarde, J.; Blasingame, T. A.; McCain Jr., W. D. (1997). "Correlation of Black Oil Properties At Pressures Below Bubble Point Pressure - A New Approach"
. Presented at the Annual Technical Meeting of CIM, Calgary, Alberta. Petroleum Society of Canada (PETSOC-97-93).
