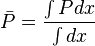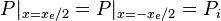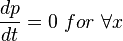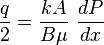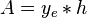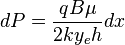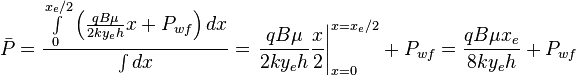Difference between revisions of "4/π stimulated well potential"
From wiki.pengtools.com
(→Math & Physics) |
(→Math & Physics) |
||
| Line 24: | Line 24: | ||
Since average pressure is: <math>\bar P = \frac{\int P dx}{\int dx}</math> | Since average pressure is: <math>\bar P = \frac{\int P dx}{\int dx}</math> | ||
| − | :<math> \bar P = \frac{ \int \limits_{0}^{x_e/2} \left ( \frac{q B \mu}{2ky_eh} x + P_{wf} \right ) dx}{\int dx} = \left. \frac{q B \mu}{2ky_eh} \frac{x}{2} \right|_{x=0}^{x=x_e/2} + P_{wf}</math> | + | :<math> \bar P = \frac{ \int \limits_{0}^{x_e/2} \left ( \frac{q B \mu}{2ky_eh} x + P_{wf} \right ) dx}{\int dx} = \left. \frac{q B \mu}{2ky_eh} \frac{x}{2} \right|_{x=0}^{x=x_e/2} + P_{wf} = \frac{q B \mu x_e}{8ky_eh} + P_{wf}</math> |
[[Category:Technology]] | [[Category:Technology]] | ||
Revision as of 09:54, 10 September 2018
Brief
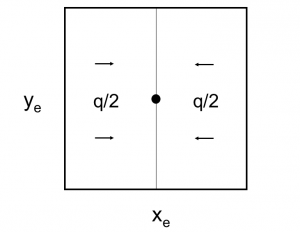
4/π is the maximum possible stimulation potential for steady state linear flow in a square well spacing.
Math & Physics
Steady state flow boundary conditions:
From Darcy's law:
Integration gives: 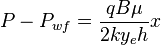
Since average pressure is: