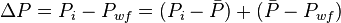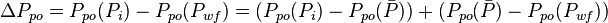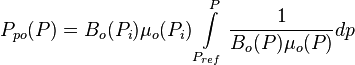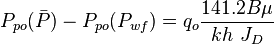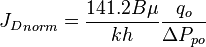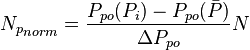Difference between revisions of "Oil Flowing Material Balance"
(→Math & Physics) |
(→Math & Physics) |
||
| Line 40: | Line 40: | ||
Finally, the [[Oil Flowing Material Balance]] equation: | Finally, the [[Oil Flowing Material Balance]] equation: | ||
| − | :<math> | + | :<math> {J_D}_{norm} = J_D - \frac{P_{po}(P_i) - {N_p}_{norm} \frac{J_D}{N}</math> |
| + | Where | ||
:<math> {J_D}_{norm} = \frac{141.2 B \mu}{kh} \frac{q_o}{\Delta P_{po}} </math> | :<math> {J_D}_{norm} = \frac{141.2 B \mu}{kh} \frac{q_o}{\Delta P_{po}} </math> | ||
Revision as of 07:03, 10 April 2018
Contents
Brief
Oil Flowing Material Balance (Oil FMB) is the advanced engineering technique published in 2005 by Louis Mattar and David Anderson [1].
Oil Flowing Material Balance is applied to determine:
- Reservoirs STOIIP & EUR
- Well's EUR and JD
Oil Flowing Material Balance uses readily available Well flowing data: production rate and bottomhole pressure.
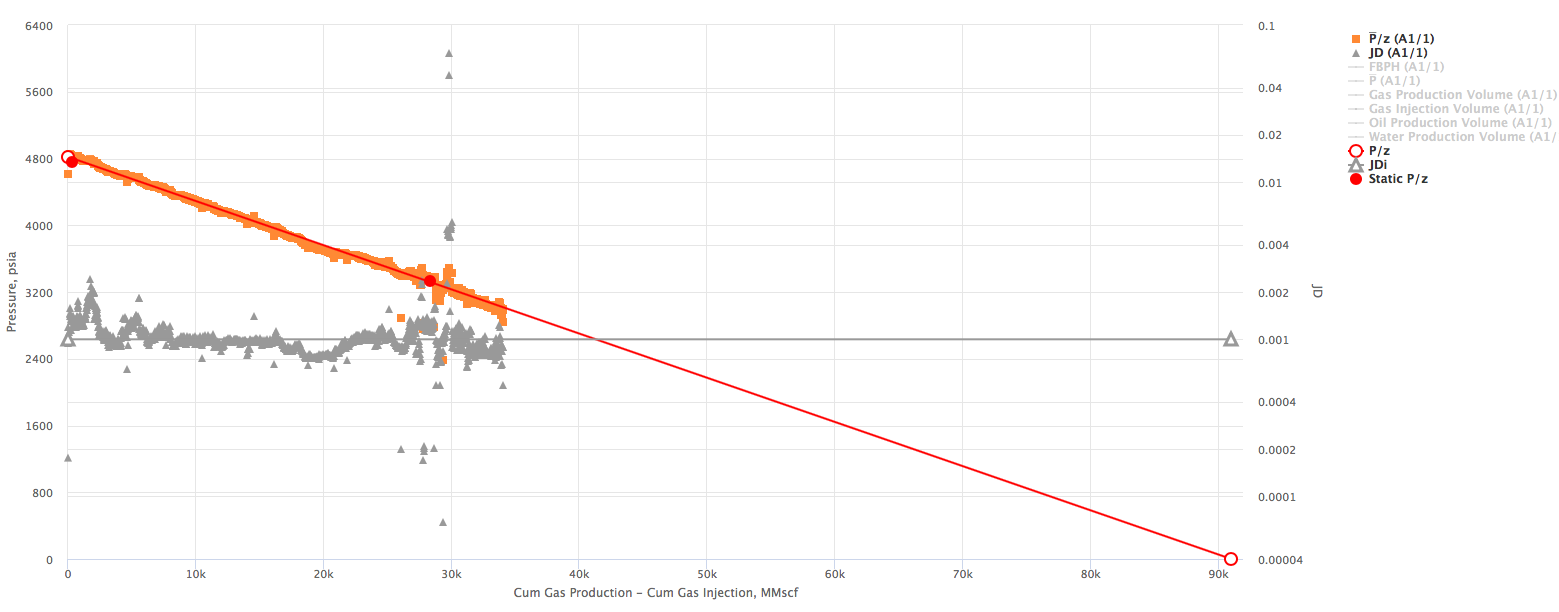
The interpretation technique is fitting the data points with the straight lines to estimate STOIIP and JD.
Math & Physics
The total pressure drop at the wellbore is:
Where
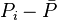 , is pressure drop due to depletion defined by the Oil Material Balance
, is pressure drop due to depletion defined by the Oil Material Balance
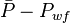 , is pressure drop due to Darcy's law
, is pressure drop due to Darcy's law
In terms of oil pseudo pressure the total pressure drop is:
Where
Finally, the Oil Flowing Material Balance equation:
- Failed to parse (syntax error): {J_D}_{norm} = J_D - \frac{P_{po}(P_i) - {N_p}_{norm} \frac{J_D}{N}
Where
Discussion
Gas Flowing Material Balance can be applied to:
- single well
- multiple wells producing from the same Reservoir.
The X axis on the Gas Flowing Material Balance Plot can be selected as:
Example 1. Multiple wells producing from the same Reservoir. X axis - Wells cumulative
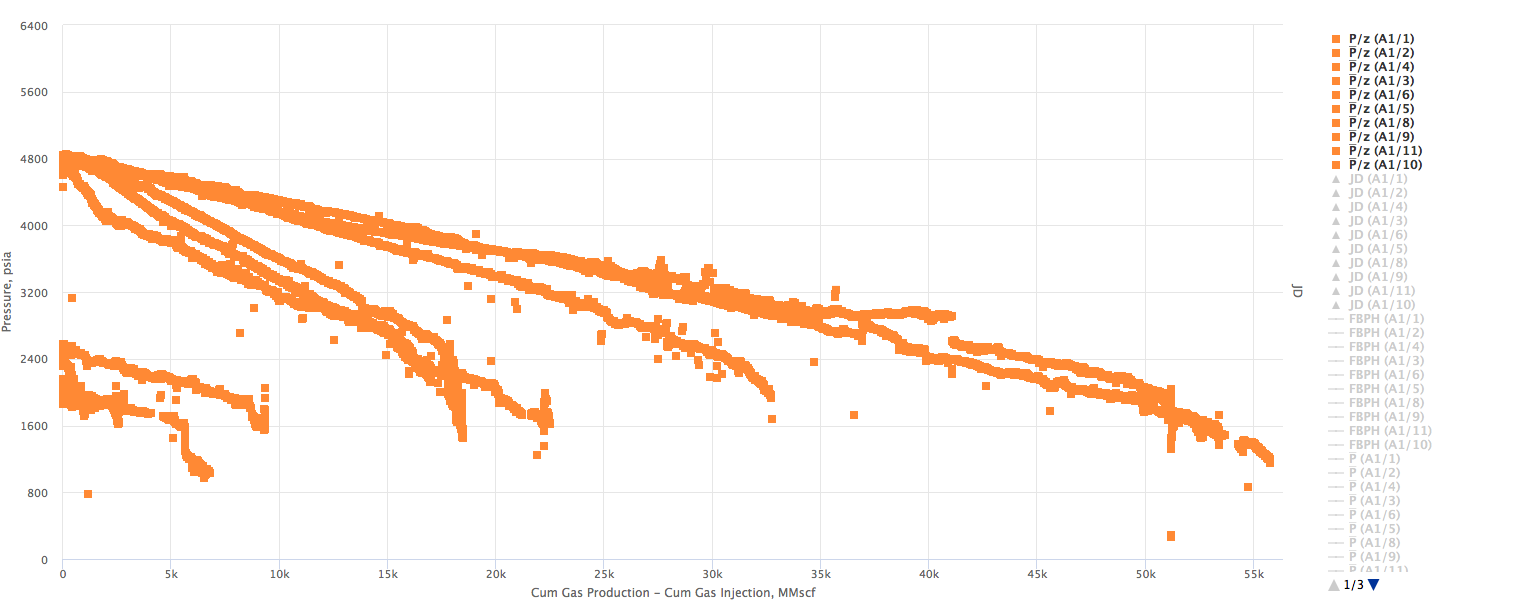 Example 2. Multiple wells producing from the same Reservoir. X axis - Reservoir cumulative
Example 2. Multiple wells producing from the same Reservoir. X axis - Reservoir cumulative
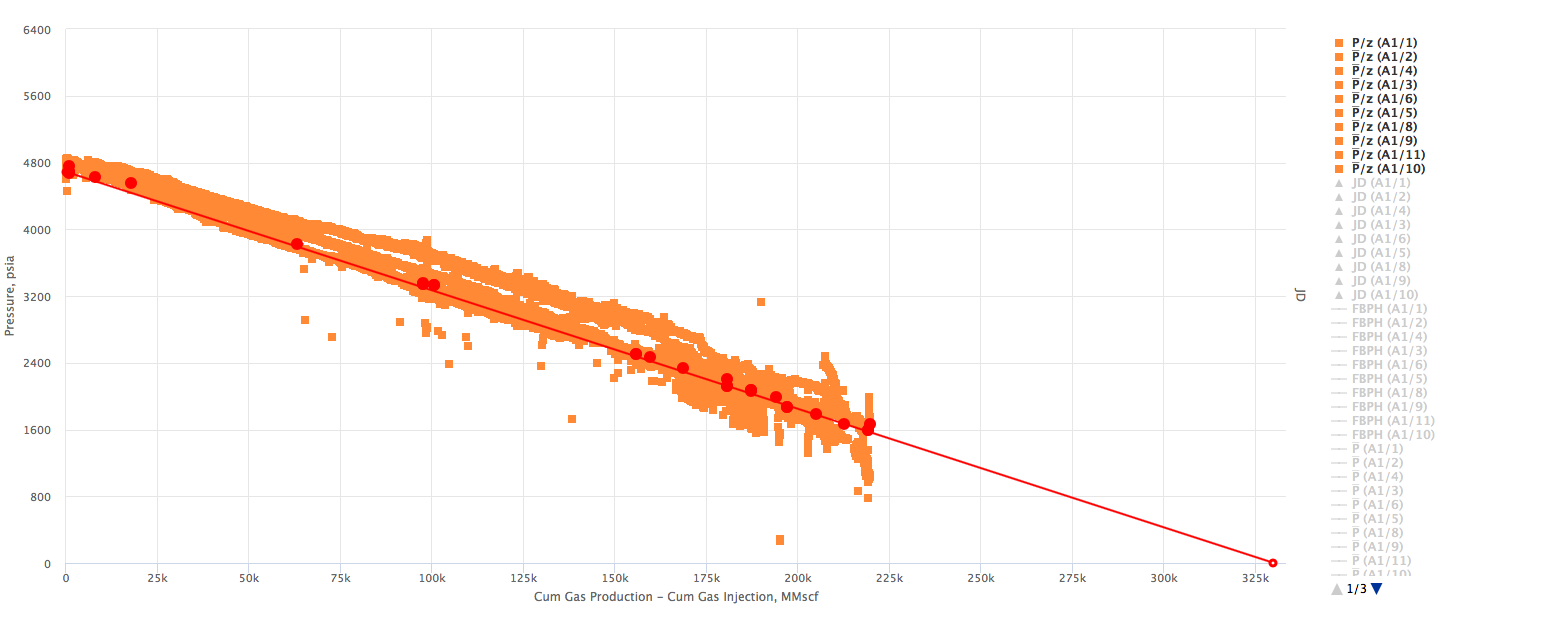 Example 3. Shifted Model Start (to account for gas injection)
Example 3. Shifted Model Start (to account for gas injection)
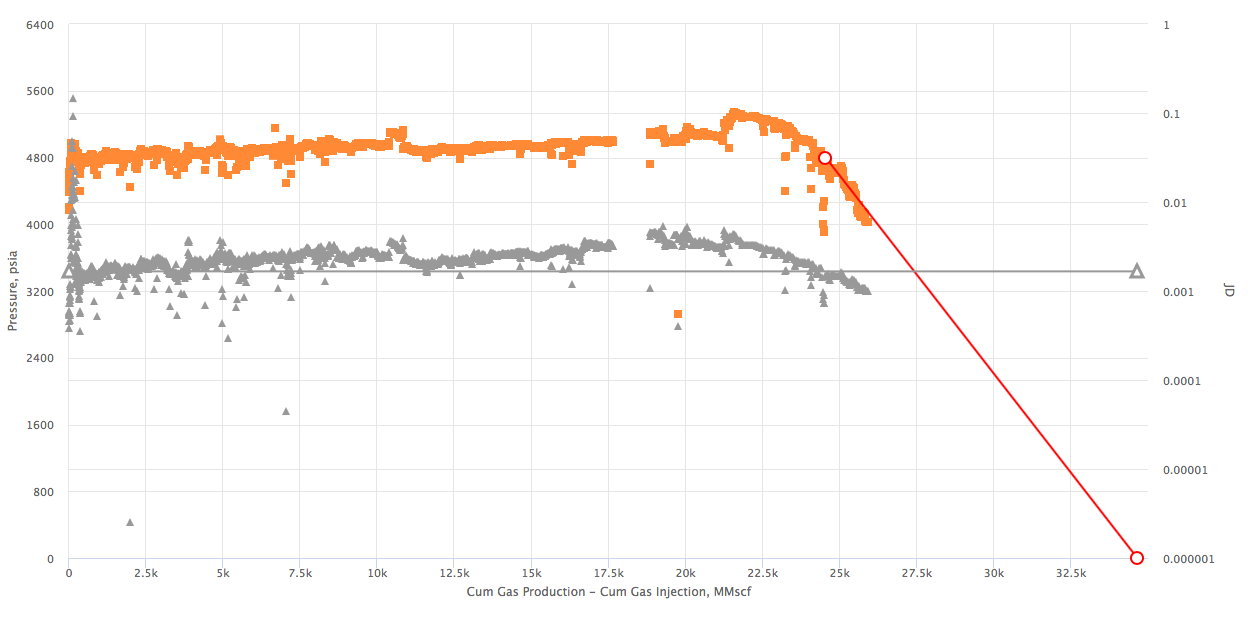
Workflow
- Upload the data required
- Open the Gas Flowing Material Balance tool here
- Calculate the red
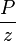 line:
line:
- Given the GIIP
- Calculate the
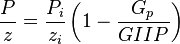
- Calculate the orange
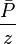 curve:
curve:
- Given the flowing wellhead pressures, calculate the flowing bottomhole pressures,
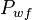
- Convert the flowing pressures to pseudopressures,
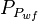
- Given the JD, calculate the
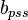
- Calculate the pseudopressure,
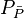
- Convert the pseudopressure to pressure,
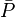
- Calculate the
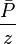
- Given the flowing wellhead pressures, calculate the flowing bottomhole pressures,
- Calculate the gray JD curve:
- Calculate the gas productivity index,
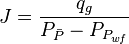
- Calculate the JD,
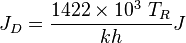
- Calculate the gas productivity index,
- Change the red
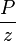 line to match the orange
line to match the orange 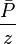 curve
curve
- Change the GIIP
- Change the intitial
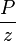
- Change the flat JD gray line to match the changing JD gray line
- Save the FMB model
- Move to the next well
Extra Plot to find bpss
- Calculate the initial pseudopressure,
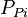
- Calculate the material balance pseudo-time,
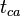
- Plot
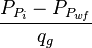 versus
versus 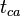
- The intercept with the Y axis gives
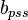 and
and 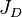
Data required
- Create Field here
- Create or Upload Reservoirs here
- Input the Reservoirs GIIP and STOIIP here
- Create or Upload PVT (SG, Pi, Ti) here
- Upload Wells
- Create or Upload Wells Perforations here
- Create or Upload kh and JD here
- Upload Daily Measures
In case you need to calculate the flowing bottomhole pressure from the wellhead pressure:
- Calculate the flowing bottomhole pressures using BHP Calculator
- Export flowing bottomhole pressures to Daily Measures here
In case you want to add the static reservoir pressures on the FMB Plot:
- Create or Upload the static reservoir pressures, here
- Calculate Monthly Measures from the Daily Measures using Monthly Data Calculator
Nomenclature
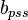 = reservoir constant, inverse to productivity index, psia2/cP/MMscfd
= reservoir constant, inverse to productivity index, psia2/cP/MMscfd = compressibility, psia-1
= compressibility, psia-1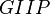 = gas initially in place, MMscf
= gas initially in place, MMscf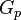 = cumulative gas produced, MMscf
= cumulative gas produced, MMscf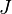 = gas productivity index, MMscfd/(psia2/cP)
= gas productivity index, MMscfd/(psia2/cP)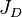 = dimensionless productivity index, dimensionless
= dimensionless productivity index, dimensionless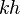 = permeability times thickness, md*m
= permeability times thickness, md*m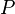 = pressure, psia
= pressure, psia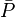 = average reservoir pressure, psia
= average reservoir pressure, psia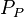 = pseudopressure, psia2/cP
= pseudopressure, psia2/cP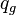 = gas rate, MMscfd
= gas rate, MMscfd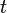 = time, day
= time, day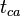 = material balance pseudotime for gas, day
= material balance pseudotime for gas, day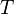 = temperature, °R
= temperature, °R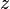 = gas compressibility factor, dimensionless
= gas compressibility factor, dimensionless
Greek symbols
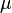 = viscosity, cp
= viscosity, cp
Subscripts
- g = gas
- i = initial
- R = °R
- wf = well flowing
References
- ↑ 1.0 1.1 Mattar, L.; Anderson, D (2005). "Dynamic Material Balance (Oil or Gas-In-Place Without Shut-Ins)" (PDF). CIPC.
- ↑ 2.0 2.1 Stalgorova, Louis; Mattar, Ekaterina (2016). "Analytical Methods for Single-Phase Oil Flow: Accounting for Changing Liquid and Rock Properties". Society of Petroleum Engineers.