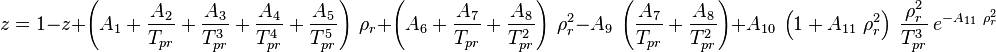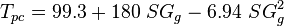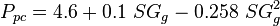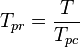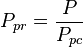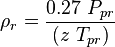Difference between revisions of "Dranchuk correlation"
From wiki.pengtools.com
Gprotsykov (talk | contribs) |
Gprotsykov (talk | contribs) |
||
| Line 56: | Line 56: | ||
=== Nomenclature === | === Nomenclature === | ||
:<math> A_1..A_{11} </math> coefficients | :<math> A_1..A_{11} </math> coefficients | ||
| + | :<math> \rho_r </math> = reduced density, dimensionless | ||
:<math> P </math> = Pressure, psia | :<math> P </math> = Pressure, psia | ||
| − | :<math> P_{pc} </math> = | + | :<math> P_{pc} </math> = pseudo critical pressure, psia |
:<math> P_{pr} </math> = pseudoreduced pressure, dimensionless | :<math> P_{pr} </math> = pseudoreduced pressure, dimensionless | ||
:<math> SG_g </math> = gas specific density, dimensionless | :<math> SG_g </math> = gas specific density, dimensionless | ||
| − | :<math> T </math> = | + | :<math> T </math> = temperature, °R |
| − | :<math> T_{pc} </math> = | + | :<math> T_{pc} </math> = pseudo critical temperature, °R |
| − | :<math> T_{pr} </math> = | + | :<math> T_{pr} </math> = pseudoreduced temperature, dimensionless |
:<math> z </math> = gas compressibility factor, dimensionless | :<math> z </math> = gas compressibility factor, dimensionless | ||
| − | |||
=== References === | === References === | ||
Revision as of 12:24, 25 April 2017
Brief
Dranchuk correlation is the fitting function of the classic Standing and Katz [1] gas compressibility factor correlation.
Math & Physics
A1 = 0.3265
A2 = –1.0700
A3 = –0.5339
A4 = 0.01569
A5 = –0.05165
A6 = 0.5475
A7 = –0.7361
A8 = 0.1844
A9 = 0.1056
A10 = 0.6134
A11 = 0.7210
where
Discussion
To avoid the Liquid loading the gas velocity should be above the Liquid loading velocity.
The higher the gas rate the higher the gas velocity.
The lower the wellhead flowing pressure the higher the gas rate.
The bigger the tubing ID the higher the gas rate.
In case when the gas rate is limited by the Reservoir deliverability smaller tubing ID will increase the gas velocity.
Nomenclature
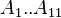 coefficients
coefficients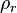 = reduced density, dimensionless
= reduced density, dimensionless = Pressure, psia
= Pressure, psia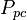 = pseudo critical pressure, psia
= pseudo critical pressure, psia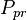 = pseudoreduced pressure, dimensionless
= pseudoreduced pressure, dimensionless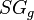 = gas specific density, dimensionless
= gas specific density, dimensionless = temperature, °R
= temperature, °R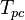 = pseudo critical temperature, °R
= pseudo critical temperature, °R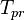 = pseudoreduced temperature, dimensionless
= pseudoreduced temperature, dimensionless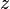 = gas compressibility factor, dimensionless
= gas compressibility factor, dimensionless
References
- ↑ Standing, M. B.; Katz, D. L. (December 1942). "Density of Natural Gases"
 . Transactions of the AIME. Society of Petroleum Engineers. 146 (SPE-942140-G).
. Transactions of the AIME. Society of Petroleum Engineers. 146 (SPE-942140-G).
- ↑ Dranchuk, P. M.; Abou-Kassem, H. (July 1975). "Calculation of Z Factors For Natural Gases Using Equations of State"
 . The Journal of Canadian Petroleum. 14 (PETSOC-75-03-03).
. The Journal of Canadian Petroleum. 14 (PETSOC-75-03-03).