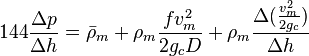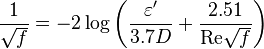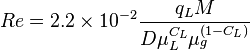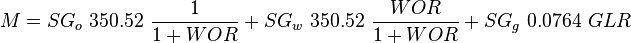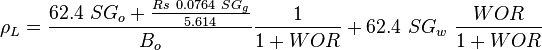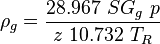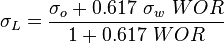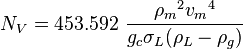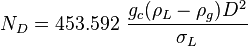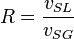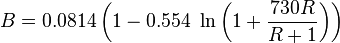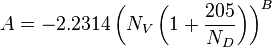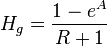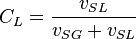Difference between revisions of "Gray correlation"

From wiki.pengtools.com
Jump to: navigation, search
(→‎Workflow Hg)
(→‎Workflow Hg)
Line 37: Line 37:
 
:<math> \rho_m = \rho_L C_L + \rho_g (1-C_L) </math>
 
:<math> \rho_m = \rho_L C_L + \rho_g (1-C_L) </math>
  
−
:<math> \sigma_L = \frac{\sigma_o + 0.617 \sigma_w WOR}{1 + 0.617 WOR}</math>
+
:<math> \sigma_L = \frac{\sigma_o + 0.617\ \sigma_w\ WOR}{1 + 0.617\ WOR}</math>
  
 
:<math> N_V = 453.592\ \frac{{\rho_m}^2 {v_m}^4}{g_c \sigma_L (\rho_L - \rho_g)} </math><ref name= Gray/>
 
:<math> N_V = 453.592\ \frac{{\rho_m}^2 {v_m}^4}{g_c \sigma_L (\rho_L - \rho_g)} </math><ref name= Gray/>

Revision as of 19:09, 4 April 2017

Brief

life is good with Gray[1]

Math & Physics

Following the law of conservation of energy the basic steady state flow equation is:

144 \frac{\Delta p}{\Delta h} = \bar \rho_m + \rho_m \frac{f v_m^2 }{2 g_c D} + \rho_m \frac{\Delta{(\frac{v_m^2}{2g_c}})}{\Delta h}[1]

where

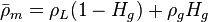\bar \rho_m = \rho_L (1-H_g) + \rho_g H_g, slip mixture density
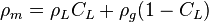\rho_m = \rho_L C_L + \rho_g (1-C_L) , no-slip mixture density

Colebrook–White [2] equation for the Darcy's friction factor:

\frac{1}{\sqrt{f}}= -2 \log \left( \frac { \varepsilon'} {3.7 D} + \frac {2.51} {\mathrm{Re} \sqrt{f}} \right)[3]

The pseudo wall roughness [1]:

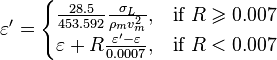\varepsilon' = \begin{cases} \frac{28.5}{453.592} \frac{\sigma_L}{\rho_m v_m^2}, &\mbox{if } R \geqslant 0.007 \\ \varepsilon + R \frac{\varepsilon'-\varepsilon}{0.0007}, & \mbox{if } R < 0.007 \end{cases} , with the limit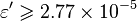 \varepsilon' \geqslant 2.77 \times 10^{-5}

Reynolds two phase number:

Re = 2.2 \times 10^{-2} \frac {q_L M}{D \mu_L^{C_L} \mu_g^{(1-C_L)}}

Discussion

Workflow Hg

M =SG_o\ 350.52\ \frac{1}{1+WOR}+SG_w\ 350.52\ \frac{WOR}{1+WOR}+SG_g\ 0.0764\ GLR[4]
\rho_L= \frac{62.4\ SG_o + \frac{Rs\ 0.0764\ SG_g}{5.614}}{B_o} \frac{1}{1+WOR} + 62.4\ SG_w\ \frac{WOR}{1 + WOR}[5]
\rho_g = \frac{28.967\ SG_g\ p}{z\ 10.732\ T_R} [5]
\rho_m = \rho_L C_L + \rho_g (1-C_L)
\sigma_L = \frac{\sigma_o + 0.617\ \sigma_w\ WOR}{1 + 0.617\ WOR}
N_V = 453.592\ \frac{{\rho_m}^2 {v_m}^4}{g_c \sigma_L (\rho_L - \rho_g)} [1]
N_D = 453.592\ \frac{g_c (\rho_L - \rho_g) D^2}{\sigma_L }
R = \frac{v_{SL}}{v_{SG}}
B = 0.0814 \left ( 1 - 0.554\ \ln \left (1 + \frac{730 R}{R+1} \right ) \right )
A = -2.2314 \left ( N_V \left (1 + \frac{205}{N_D} \right ) \right )^B
H_g = \frac{1-e^A}{R+1}
C_L = \frac{v_{SL}}{v_{SG}+v_{SL}}

Nomenclature

NV velocity number

References

  1. ↑ 1.0 1.1 1.2 1.3 Gray, H. E. (1974). "Vertical Flow Correlation in Gas Wells". User manual for API 14B, Subsurface controlled safety valve sizing computer program. API. 
  2. ↑ Colebrook, C. F. (1938–1939). "Turbulent Flow in Pipes, With Particular Reference to the Transition Region Between the Smooth and Rough Pipe Laws"Paid subscription required. Journal of the Institution of Civil Engineers. London, England. 11: 133–156. 
  3. ↑ Moody, L. F. (1944). "Friction factors for pipe flow"Paid subscription required. Transactions of the ASME. 66 (8): 671–684. 
  4. ↑ Cite error: Invalid <ref> tag; no text was provided for refs named HB
  5. ↑ 5.0 5.1 Cite error: Invalid <ref> tag; no text was provided for refs named Lyons
Retrieved from "https://wiki.pengtools.com/index.php?title=Gray_correlation&oldid=1885"