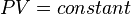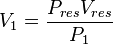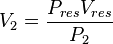Difference between revisions of "Can Of Beans (Gas)"
(→Math and Physics) |
(→Math and Physics) |
||
| Line 50: | Line 50: | ||
:<math> PV = constant = P_1V_1 = P_2V_2=P_{res}V_{res}</math> | :<math> PV = constant = P_1V_1 = P_2V_2=P_{res}V_{res}</math> | ||
| + | |||
| + | The gas produced volume of the "Slow case" | ||
| + | :<math> V_1 = \frac{P_{res}V_{res}}{P_1}</math> | ||
| + | |||
| + | The gas produced volume of the "Fast case" | ||
| + | :<math> V_2 = \frac{P_{res}V_{res}}{P_2}</math> | ||
==Well Nodal Analysis Example== | ==Well Nodal Analysis Example== | ||
Revision as of 07:58, 12 December 2022
Contents
Brief
A case study on how to increase the gas recovery factor by increasing the gas production rates.
Have you ever heard that if you increase the choke size on a gas well, the well will "die" soon, because of the water? And gas recovery will go down too?
What if you could increase the gas production and recover more gas instead?
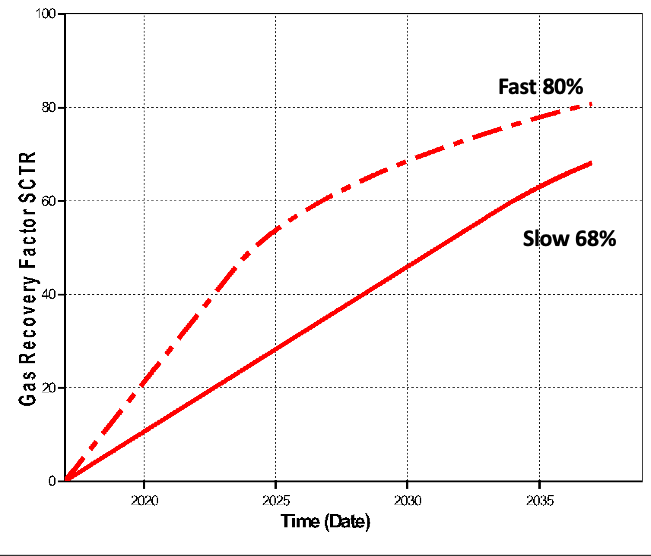
This case study clearly demonstrates that gas recovery is increased with increasing the gas rate.
It is shown that enhanced well will add more reserves then non-enhanced well.
Case study is done using the simulation model assuring physics is well governed.
Can of beans analogy
If you eat the can of beans fast then the can doesn’t last as long as if you eat it slow, but you still eat the same amount of beans.
Same logic is true for the gas reservoir with the bottom water.
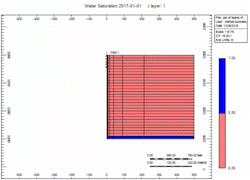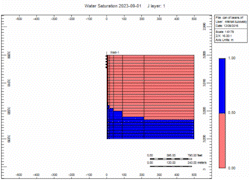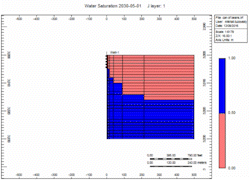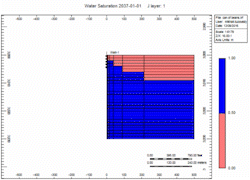
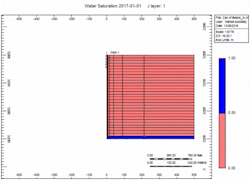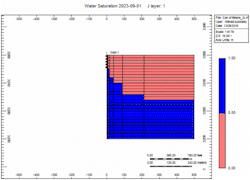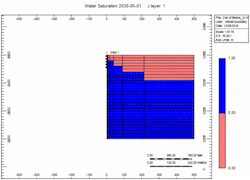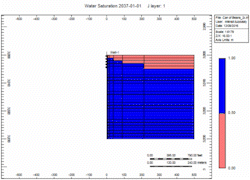
There is a fixed volume of gas above the water. When you remove the gas the water moves up. You can do it slow or fast but the volume of gas above the water is the same. The water level will raise Gravity stable as defined by Newton’s Law.
Simulation Runs
Now let's attach the infinite aquifer to the can of gas and run scenarios:
- Slow - choked gas rate
- Fast - 2x enhanced gas rate
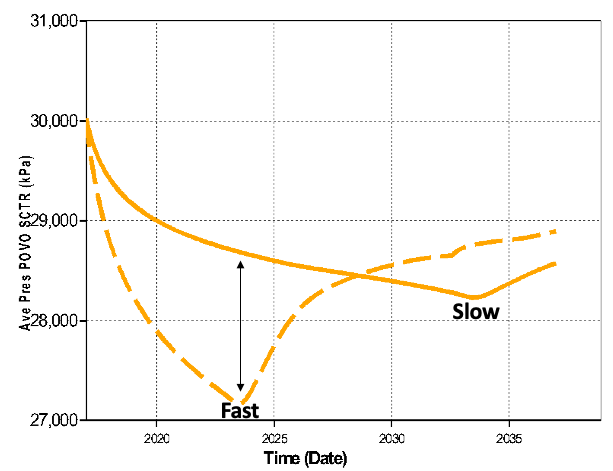
Oh no, water killed the well quick in the "Fast" case! We told you what! Right, but … which case produced more gas?
Gas Recovery
12% more recovery with the enhanced production over 20 years. Why?
Because of the pressure! The lower the reservoir pressure the more gas is produced before the water hits the perfs. It’s just physics!
Math and Physics
According to the Boyle's law (1662):
where P is pressure, V is volume.
In our case
The gas produced volume of the "Slow case"
The gas produced volume of the "Fast case"
Well Nodal Analysis Example
Given data[1]:
SGg=0.65, SGo=35 API, Pr=2200 psi, Pb=1800 psi, Tr=140 F, depth = 5000ft, tubing size = 2 3/8 in OD, GOR=400 scf/stb, WOR=0 Productivity index J = 1 bbl/d/psi
It's required to find the well flowing rate at the wellhead pressure of 230 psi. Surface flow line and separator are not in question.
Solution at bottom of well
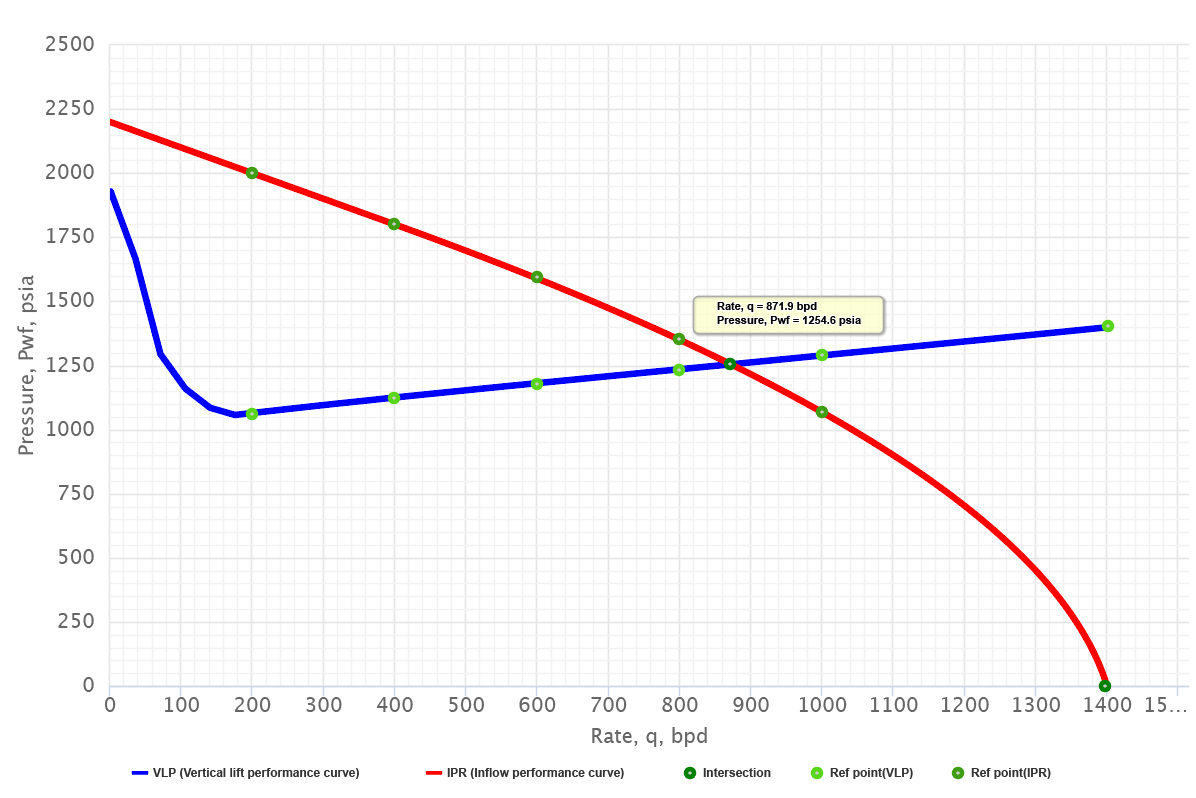
In order to solve for the flow rate at bottomhole (node position 6), the entire system is divided into two components, the reservoir or well capability component, IPR and the piping system component, VLP [2].
- First, Vogel's equation is used to calculate the IPR curve. The AOF = 1400 bbl/d
| Rate, bbl/d | Pwf, psi |
|---|---|
| 0 | 2200 |
| 200 | 2000 |
| 400 | 1800 |
| 600 | 1590 |
| 800 | 1350 |
| 1000 | 1067 |
| 1400 | 0 |
- Second, Hagedorn and Brown multiphase flow correlation is used to calculate the required tubing intake pressures at the given wellhead pressure, VLP curve.
| Rate, bbl/d | Pwf, psi |
|---|---|
| 0 | 1929 |
| 200 | 1065 |
| 400 | 1125 |
| 600 | 1181 |
| 800 | 1235 |
| 1000 | 1289 |
| 1400 | 1399 |
- Third, IPR and VLP curves are plotted on the pressure vs rate plot. The intersection of these two curves shows the flow rate to be 872 bbl/d.
This is "the rate" possible for this system. It is not a maximum, minimum, or optimum but is the rate at which this well will produce for the piping system installed. The rate can be changed only by changing something in the system - that is, pipe sizes, choke or by shifting the IPR curve through simulation treatment.— Kermit Brown et al [2]
See also
References
- ↑
Mach, Joe; Proano, Eduardo; Brown, Kermit E. (1979). "A Nodal Approach For Applying Systems Analysis To The Flowing And Artificial Lift Oil Or Gas Well"
 (SPE-8025-MS). Society of Petroleum Engineers.
(SPE-8025-MS). Society of Petroleum Engineers.
- ↑ 2.0 2.1 Brown, Kermit (1984). The Technology of Artificial Lift Methods. Volume 4. Production Optimization of Oil and Gas Wells by Nodal System Analysis. Tulsa, Oklahoma: PennWellBookss.
Cite error: <ref> tag with name "Legends" defined in <references> is not used in prior text.