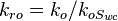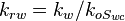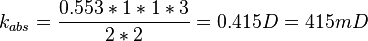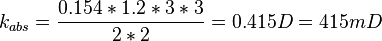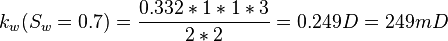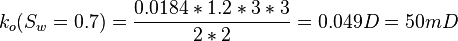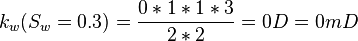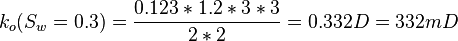Difference between revisions of "Relative Permeability"
| Line 26: | Line 26: | ||
Core dimensions: A=2 cm2, L=3 cm. PVT: water viscosity = 1 cP, oil viscosity = 3 cP, Bw=1 cc/cc, Bo=1.2 cc/cc. | Core dimensions: A=2 cm2, L=3 cm. PVT: water viscosity = 1 cP, oil viscosity = 3 cP, Bw=1 cc/cc, Bo=1.2 cc/cc. | ||
| + | ===Absolute permeability=== | ||
| + | |||
Core is at 100% water and qw=0.553 cc/sec: | Core is at 100% water and qw=0.553 cc/sec: | ||
| Line 35: | Line 37: | ||
:<math> k_{abs} = \frac{0.154*1.2*3*3}{2*2} = 0.415 D = 415 mD </math> | :<math> k_{abs} = \frac{0.154*1.2*3*3}{2*2} = 0.415 D = 415 mD </math> | ||
| + | |||
| + | === Effective permeability=== | ||
Same core at 70% water and 30% oil and qw=0.332 cc/sec and qo=0.0184 cc/sec: | Same core at 70% water and 30% oil and qw=0.332 cc/sec and qo=0.0184 cc/sec: | ||
| Line 46: | Line 50: | ||
:<math> k_o(S_w=0.3)= \frac{0.123*1.2*3*3}{2*2} = 0.332 D = 332 mD </math> | :<math> k_o(S_w=0.3)= \frac{0.123*1.2*3*3}{2*2} = 0.332 D = 332 mD </math> | ||
| − | + | === Relative permeability=== | |
In this case the mobility of water is 15 times higher than the mobility of water. | In this case the mobility of water is 15 times higher than the mobility of water. | ||
Revision as of 16:50, 30 March 2022
Contents
Brief
Relative Permeability is the ratio of the effective permeability to base oil permeability measured at connate water saturation[1].
where
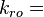 Oil relative permeability, fraction
Oil relative permeability, fraction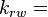 Water relative permeability, fraction
Water relative permeability, fraction 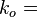 Effective water permeability, mD
Effective water permeability, mD 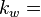 Effective water permeability, mD
Effective water permeability, mD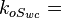 Effective oil permeability at irreducible oil saturation, mD
Effective oil permeability at irreducible oil saturation, mD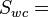 Connate water saturation, fraction
Connate water saturation, fraction
Related definitions
Effective permeability - oil, water, gas phase permeability when more than one phase is present. Depends on fluids saturations.
Absolute permeability - permeability of the core sample when saturated with one liquid. Independent of fluid. Dependent on pore throat sizes.
Example
Determine the Relative Permeability using the following data[1]:
Core dimensions: A=2 cm2, L=3 cm. PVT: water viscosity = 1 cP, oil viscosity = 3 cP, Bw=1 cc/cc, Bo=1.2 cc/cc.
Absolute permeability
Core is at 100% water and qw=0.553 cc/sec:
Using Darcy's law:
Same core at 100% oil and qo=0.154 cc/sec:
Effective permeability
Same core at 70% water and 30% oil and qw=0.332 cc/sec and qo=0.0184 cc/sec:
Same core at 30% water and 70% oil and qw=0 cc/sec and qo=0.123 cc/sec:
Relative permeability
In this case the mobility of water is 15 times higher than the mobility of water.
See Also
References
- ↑ 1.0 1.1
Wolcott, Don (2009). Applied Waterflood Field Development
 . Houston: Energy Tribune Publishing Inc.
. Houston: Energy Tribune Publishing Inc.