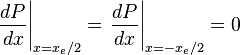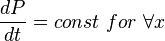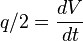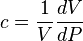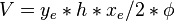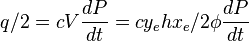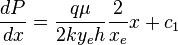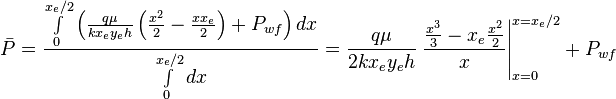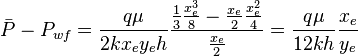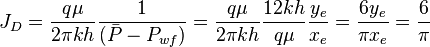Difference between revisions of "6/π stimulated well potential"

From wiki.pengtools.com
Jump to: navigation, search
(→‎See also)
(→‎Nomenclature)
Line 61: Line 61:
  
 
:<math> A </math> = cross-sectional area, cm2
 
:<math> A </math> = cross-sectional area, cm2
 +
:<math> c</math> = total compressibility, atm-1
 
:<math> h </math> = thickness, m
 
:<math> h </math> = thickness, m
 +
:<math> J_D</math> = dimensionless productivity index, dimensionless
 
:<math> k</math> = permeability, d
 
:<math> k</math> = permeability, d
 
:<math> P </math> = pressure, atm
 
:<math> P </math> = pressure, atm
Line 68: Line 70:
 
:<math> \bar P</math> = average pressure, atm
 
:<math> \bar P</math> = average pressure, atm
 
:<math> q </math> = flow rate, cm<sup>3</sup>/sec
 
:<math> q </math> = flow rate, cm<sup>3</sup>/sec
 +
:<math> V</math> = one wing volume, m3
 
:<math> x </math> = length, m
 
:<math> x </math> = length, m
 
:<math> x_e</math> = drinage area length, m
 
:<math> x_e</math> = drinage area length, m
 
:<math> y_e</math> = drinage area width, m
 
:<math> y_e</math> = drinage area width, m
−
:<math> V</math> = one wing volume, m3
 
−
:<math> c</math> = total compressibility, atm-1
 
−
:<math> J_D</math> = dimensionless productivity index, dimensionless
 
  
 
===Greek symbols===
 
===Greek symbols===

Revision as of 10:55, 12 September 2018

Brief

Stimulated well drainage

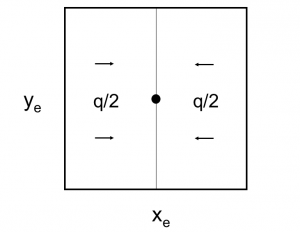
6/π is the maximum possible stimulation potential for pseudo steady state linear flow in a square well spacing.

Math & Physics

Pseudo steady state flow boundary conditions:

\left. \frac{dP}{dx} \right|_{x=x_e/2} = \left. \frac{dP}{dx} \right|_{x=-x_e/2} = 0
\frac{dP}{dt} =const\ for \ \forall x

From Diffusivity Equation:

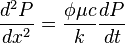\frac{d^2P}{dx^2}=\frac{\phi \mu c}{k} \frac{dP}{dt} ( 1 )

From Material Balance:

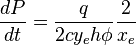q/2 =\frac{dV}{dt}
c=\frac{1}{V} \frac{dV}{dP}
V =y_e*h*x_e/2*\phi
q/2 =c V\frac{dP}{dt} = c y_e h x_e/2 \phi \frac{dP}{dt}
\frac{dP}{dt} = \frac{q}{2 c y_e h \phi} \frac{2}{x_e} ( 2 )

( 2 ) - > ( 1 ) :

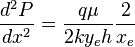\frac{d^2P}{dx^2}=\frac{q \mu}{2 k y_e h} \frac{2}{x_e} ( 3 )

Integrating ( 3 ):

\frac{dP}{dx}=\frac{q \mu}{2 k y_e h} \frac{2}{x_e} x + c_1
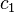c_1 must satisfy boundary condition: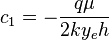 c_1 = - \frac{q \mu}{2 k y_e h}
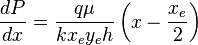\frac{dP}{dx}=\frac{q \mu}{k x_e y_e h} \left ( x- \frac{x_e}{2} \right ) ( 4 )

Integrating ( 4 ):

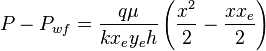P - P_{wf} = \frac{q \mu}{k x_e y_e h} \left ( \frac{x^2}{2} - \frac{x x_e}{2} \right ) ( 5 )

Since average pressure is: 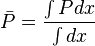\bar P = \frac{\int P dx}{\int dx}:

\bar P = \frac{ \int \limits_{0}^{x_e/2} \left ( \frac{q \mu}{k x_e y_e h} \left ( \frac{x^2}{2} - \frac{x x_e}{2} \right ) + P_{wf} \right ) dx}{\int \limits_{0}^{x_e/2}dx} = \frac{q \mu}{2 k x_e y_e h} \left. \frac{\frac{x^3}{3} - x_e \frac{x^2}{2}}{x} \right|_{x=0}^{x=x_e/2} + P_{wf}
\bar P - P_{wf} = \frac{q \mu}{2 k x_e y_e h} \frac{\frac{1}{3} \frac{x_e^3}{8} -\frac{x_e}{2} \frac{x_e^2}{4}}{\frac{x_e}{2}} = \frac{q \mu}{12 k h} \frac{x_e}{y_e}
J_D=\frac{q \mu}{2 \pi k h} \frac{1}{( \bar P - P_{wf})} =\frac{q \mu}{2 \pi k h} \frac{12 k h}{q \mu} \frac{y_e}{x_e} = \frac{6 y_e}{\pi x_e}=\frac{6}{\pi}

See also

JD
optiFrac
fracDesign
Production Potential

Nomenclature

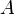A = cross-sectional area, cm2
c = total compressibility, atm-1
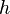h = thickness, m
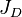J_D = dimensionless productivity index, dimensionless
k = permeability, d
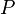P = pressure, atm
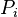P_i = initial pressure, atm
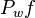P_wf = well flowing pressure, atm
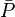\bar P = average pressure, atm
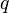q = flow rate, cm3/sec
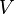V = one wing volume, m3
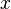x = length, m
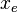x_e = drinage area length, m
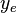y_e = drinage area width, m

Greek symbols

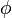\phi = porosity, fraction
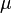\mu = oil viscosity, cp
Retrieved from "https://wiki.pengtools.com/index.php?title=6/π_stimulated_well_potential&oldid=4799"