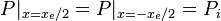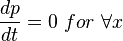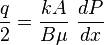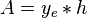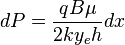Difference between revisions of "4/π stimulated well potential"
From wiki.pengtools.com
(→Math & Physics) |
(→Math & Physics) |
||
| Line 24: | Line 24: | ||
Since average pressure is: <math>\bar P = \frac{\int P dx}{\int dx}</math> | Since average pressure is: <math>\bar P = \frac{\int P dx}{\int dx}</math> | ||
| − | :<math> \bar P = \frac{ \int \limits_{0}^{x_e/2} \left ( \frac{q B \mu}{2ky_eh} x + P_{wf} \right ) dx}{\int dx} = \frac{q B \mu}{2ky_eh} \frac{x}{2} \ | + | :<math> \bar P = \frac{ \int \limits_{0}^{x_e/2} \left ( \frac{q B \mu}{2ky_eh} x + P_{wf} \right ) dx}{\int dx} = \frac{q B \mu}{2ky_eh} \frac{x}{2} | \limits_{0}^{1} + P_{wf}</math> |
Revision as of 09:49, 10 September 2018
Brief
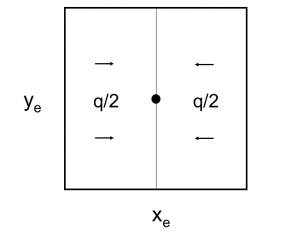
4/π is the maximum possible stimulation potential for steady state linear flow in a square well spacing.
Math & Physics
Steady state flow boundary conditions:
From Darcy's law:
Integration gives: 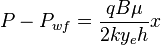
Since average pressure is: 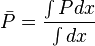
- Failed to parse (PNG conversion failed; check for correct installation of latex and dvipng (or dvips + gs + convert)): \bar P = \frac{ \int \limits_{0}^{x_e/2} \left ( \frac{q B \mu}{2ky_eh} x + P_{wf} \right ) dx}{\int dx} = \frac{q B \mu}{2ky_eh} \frac{x}{2} | \limits_{0}^{1} + P_{wf}