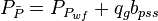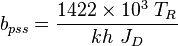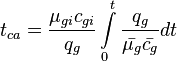Difference between revisions of "Gas Flowing Material Balance"
From wiki.pengtools.com
(→Extra Plot to find bsss) |
(→Extra Plot to find bsss) |
||
| Line 52: | Line 52: | ||
#Plot <math>\frac{P_{P_i}-P_{P_{wf}}}{q}</math> versus <math>t_{ca}</math> | #Plot <math>\frac{P_{P_i}-P_{P_{wf}}}{q}</math> versus <math>t_{ca}</math> | ||
#The intercept gives <math>b_{pss}</math> and <math>J_D</math> | #The intercept gives <math>b_{pss}</math> and <math>J_D</math> | ||
| − | |||
=== Data required === | === Data required === | ||
Revision as of 08:48, 11 December 2017
Contents
Brief
Gas Flowing Material Balance is the advanced engineering technique to determine the Reservoirs GIIP and recovery as well as Well's EUR and JD.
Gas Flowing Material Balance is applied on the Well level given readily available well flowing data: production rate and tubing head pressure.
The interpretation technique is fitting the data points with the straight line to estimate GIIP and JD.
Math & Physics
Combining the gas pseudo state flow equation and the Gas Material Balance equation to get Gas Flowing Material Balance equation:
where
Material balance pseudo-time:
Discussion
well vs reservoir model start
Workflow
- Calculate the red
 line:
line:
- Given the GIIP
- Calculate
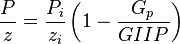
- Calculate the orange
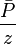 curve:
curve:
- Given the flowing wellhead pressures, calculate the flowing bottomhole pressures,
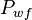
- Convert the flowing pressures to pseudopressures,
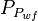
- Given the JD, calculate the
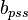
- Calculate the pseudopressure,
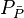
- Convert the pseudopressure to pressure,
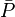
- Calculate the
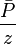
- Given the flowing wellhead pressures, calculate the flowing bottomhole pressures,
- Calculate the gray JD curve:
- Calculate the gas productivity index,
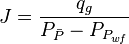
- Calculate the JD,
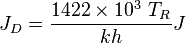
- Calculate the gas productivity index,
- Change the red
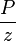 line to match the orange
line to match the orange 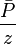 curve
curve
- Change the GIIP
- Change the intitial
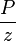
- Change the flat JD gray line to match the changing JD gray line
- Save the Gas Flowing Material Balance model
- Move to the next well
Extra Plot to find bsss
- Calculate the initial pseudopressure,
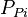
- Calculate material balance pseudo-time,
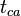
- Plot
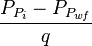 versus
versus 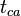
- The intercept gives
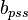 and
and 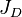
Data required
Nomenclature
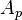 = flow area, ft2
= flow area, ft2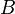 = correlation group, dimensionless
= correlation group, dimensionless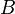 = formation factor, bbl/stb
= formation factor, bbl/stb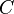 = coefficient for liquid viscosity number, dimensionless
= coefficient for liquid viscosity number, dimensionless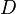 = pipe diameter, ft
= pipe diameter, ft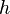 = depth, ft
= depth, ft = correlation group, dimensionless
= correlation group, dimensionless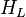 = liquid holdup factor, dimensionless
= liquid holdup factor, dimensionless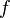 = friction factor, dimensionless
= friction factor, dimensionless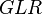 = gas-liquid ratio, scf/bbl
= gas-liquid ratio, scf/bbl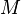 = total mass of oil, water and gas associated with 1 bbl of liquid flowing into and out of the flow string, lbm/bbl
= total mass of oil, water and gas associated with 1 bbl of liquid flowing into and out of the flow string, lbm/bbl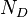 = pipe diameter number, dimensionless
= pipe diameter number, dimensionless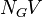 = gas velocity number, dimensionless
= gas velocity number, dimensionless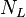 = liquid viscosity number, dimensionless
= liquid viscosity number, dimensionless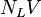 = liquid velocity number, dimensionless
= liquid velocity number, dimensionless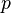 = pressure, psia
= pressure, psia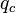 = conversion constant equal to 32.174049, lbmft / lbfsec2
= conversion constant equal to 32.174049, lbmft / lbfsec2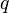 = total liquid production rate, bbl/d
= total liquid production rate, bbl/d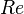 = Reynolds number, dimensionless
= Reynolds number, dimensionless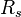 = solution gas-oil ratio, scf/stb
= solution gas-oil ratio, scf/stb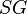 = specific gravity, dimensionless
= specific gravity, dimensionless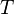 = temperature, °R or °K, follow the subscript
= temperature, °R or °K, follow the subscript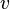 = velocity, ft/sec
= velocity, ft/sec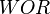 = water-oil ratio, bbl/bbl
= water-oil ratio, bbl/bbl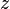 = gas compressibility factor, dimensionless
= gas compressibility factor, dimensionless
Greek symbols
 = absolute roughness, ft
= absolute roughness, ft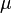 = viscosity, cp
= viscosity, cp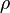 = density, lbm/ft3
= density, lbm/ft3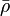 = integrated average density at flowing conditions, lbm/ft3
= integrated average density at flowing conditions, lbm/ft3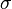 = surface tension of liquid-air interface, dynes/cm (ref. values: 72 - water, 35 - oil)
= surface tension of liquid-air interface, dynes/cm (ref. values: 72 - water, 35 - oil)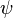 = secondary correlation factor, dimensionless
= secondary correlation factor, dimensionless
Subscripts
- g = gas
- K = °K
- L = liquid
- m = gas/liquid mixture
- o = oil
- R = °R
- SL = superficial liquid
- SG = superficial gas
- w = water
References
- ↑ Mattar, L.; Anderson, D (2005). "Dynamic Material Balance (Oil or Gas-In-Place Without Shut-Ins)" (PDF). CIPC.