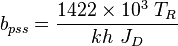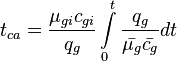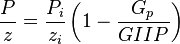Difference between revisions of "Gas Flowing Material Balance"
(→Workflow) |
|||
| Line 28: | Line 28: | ||
##<math> \frac{P}{z}=\frac{P_i}{z_i} \left (1- \frac{G_p}{GIIP}\right )</math> | ##<math> \frac{P}{z}=\frac{P_i}{z_i} \left (1- \frac{G_p}{GIIP}\right )</math> | ||
# Calculate the orange <math> \frac{\bar{P}}{z}</math> curve: | # Calculate the orange <math> \frac{\bar{P}}{z}</math> curve: | ||
| − | |||
## Calculate flowing bottomhole pressures, given flowing wellhead pressures, <math>P_{wf}</math> | ## Calculate flowing bottomhole pressures, given flowing wellhead pressures, <math>P_{wf}</math> | ||
## Calculate the flowing pseudopressures, <math>P_{P_{wf}}</math> | ## Calculate the flowing pseudopressures, <math>P_{P_{wf}}</math> | ||
##<math> P_{\bar{P}}= P_{P_{wf}} + q_g b_{pss}</math> | ##<math> P_{\bar{P}}= P_{P_{wf}} + q_g b_{pss}</math> | ||
| − | + | ===later=== | |
| − | + | Calculate initial pseudopressure, <math>P_{Pi}</math> | |
| − | + | Calculate material balance pseudo-time, <math>t_{ca}</math> | |
| − | + | Plot <math>\frac{P_{P_i}-P_{P_{wf}}}{q}</math> versus <math>t_{ca}</math>. The intercept gives <math>b_{pss}</math> and <math>J_D</math>. | |
| + | Calculate the average reservoir pseudopressure from [[Gas Flowing Material Balance]] equation, <math>P_{\bar{P}}</math> | ||
=== Data required === | === Data required === | ||
Revision as of 07:54, 11 December 2017
Contents
Brief
Gas Flowing Material Balance is the advanced engineering technique to determine the Reservoirs GIIP and recovery as well as Well's EUR and JD.
Gas Flowing Material Balance is applied on the Well level given readily available well flowing data: production rate and tubing head pressure.
The interpretation technique is fitting the data points with the straight line to estimate GIIP and JD.
Math & Physics
Combining the gas pseudo state flow equation and the Gas Material Balance equation to get Gas Flowing Material Balance equation:
where
Material balance pseudo-time:
Discussion
Workflow
- Calculate the red P/z line:
- Calculate the orange
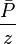 curve:
curve:
- Calculate flowing bottomhole pressures, given flowing wellhead pressures,
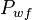
- Calculate the flowing pseudopressures,
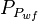
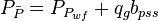
- Calculate flowing bottomhole pressures, given flowing wellhead pressures,
later
Calculate initial pseudopressure, 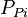 Calculate material balance pseudo-time,
Calculate material balance pseudo-time, 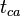 Plot
Plot 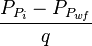 versus
versus 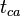 . The intercept gives
. The intercept gives 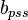 and
and 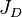 .
Calculate the average reservoir pseudopressure from Gas Flowing Material Balance equation,
.
Calculate the average reservoir pseudopressure from Gas Flowing Material Balance equation, 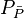
Data required
Nomenclature
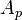 = flow area, ft2
= flow area, ft2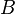 = correlation group, dimensionless
= correlation group, dimensionless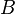 = formation factor, bbl/stb
= formation factor, bbl/stb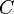 = coefficient for liquid viscosity number, dimensionless
= coefficient for liquid viscosity number, dimensionless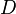 = pipe diameter, ft
= pipe diameter, ft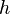 = depth, ft
= depth, ft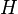 = correlation group, dimensionless
= correlation group, dimensionless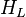 = liquid holdup factor, dimensionless
= liquid holdup factor, dimensionless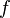 = friction factor, dimensionless
= friction factor, dimensionless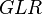 = gas-liquid ratio, scf/bbl
= gas-liquid ratio, scf/bbl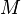 = total mass of oil, water and gas associated with 1 bbl of liquid flowing into and out of the flow string, lbm/bbl
= total mass of oil, water and gas associated with 1 bbl of liquid flowing into and out of the flow string, lbm/bbl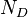 = pipe diameter number, dimensionless
= pipe diameter number, dimensionless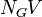 = gas velocity number, dimensionless
= gas velocity number, dimensionless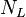 = liquid viscosity number, dimensionless
= liquid viscosity number, dimensionless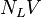 = liquid velocity number, dimensionless
= liquid velocity number, dimensionless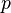 = pressure, psia
= pressure, psia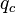 = conversion constant equal to 32.174049, lbmft / lbfsec2
= conversion constant equal to 32.174049, lbmft / lbfsec2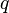 = total liquid production rate, bbl/d
= total liquid production rate, bbl/d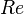 = Reynolds number, dimensionless
= Reynolds number, dimensionless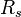 = solution gas-oil ratio, scf/stb
= solution gas-oil ratio, scf/stb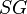 = specific gravity, dimensionless
= specific gravity, dimensionless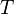 = temperature, °R or °K, follow the subscript
= temperature, °R or °K, follow the subscript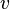 = velocity, ft/sec
= velocity, ft/sec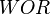 = water-oil ratio, bbl/bbl
= water-oil ratio, bbl/bbl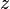 = gas compressibility factor, dimensionless
= gas compressibility factor, dimensionless
Greek symbols
 = absolute roughness, ft
= absolute roughness, ft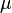 = viscosity, cp
= viscosity, cp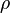 = density, lbm/ft3
= density, lbm/ft3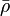 = integrated average density at flowing conditions, lbm/ft3
= integrated average density at flowing conditions, lbm/ft3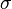 = surface tension of liquid-air interface, dynes/cm (ref. values: 72 - water, 35 - oil)
= surface tension of liquid-air interface, dynes/cm (ref. values: 72 - water, 35 - oil)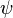 = secondary correlation factor, dimensionless
= secondary correlation factor, dimensionless
Subscripts
- g = gas
- K = °K
- L = liquid
- m = gas/liquid mixture
- o = oil
- R = °R
- SL = superficial liquid
- SG = superficial gas
- w = water
References
- ↑ Mattar, L.; Anderson, D (2005). "Dynamic Material Balance (Oil or Gas-In-Place Without Shut-Ins)" (PDF). CIPC.