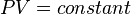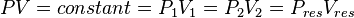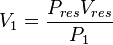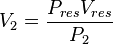Difference between revisions of "Reservoir simulator benchmark tests"

Latest revision as of 17:27, 7 August 2023

Brief

Before running any 3D reservoir simulator for a full scale field history matching or forecasts it is a good practice to make sure that the simulator is performing well on a simple benchmark tests with the well known analytical solutions.

By running those cases you could get ahead of the learning curve and gain confidence in your simulation results.

Calculating well potential

Analytical equations are available to calculate the flow rate potential for unstimulated and stimulated wells. Steady state and pseudo steady state flow regimes are considered.

Simulation Test Runs

Vertical well in a square drainage area pseudo steady state flow
Vertical well in a square drainage area steady state flow
Fracture vertical well in a square drainage area pseudo steady state flow
Fractured vertical well in a square drainage area steady state flow
Horizontal well in a square drainage area pseudo steady state flow
Horizontal well in a square drainage area steady state flow
Horizontal well with orthogonal fractures in a rectangular drainage area pseudo steady state flow
Horizontal well with orthogonal fractures in a rectangular drainage area steady state flow

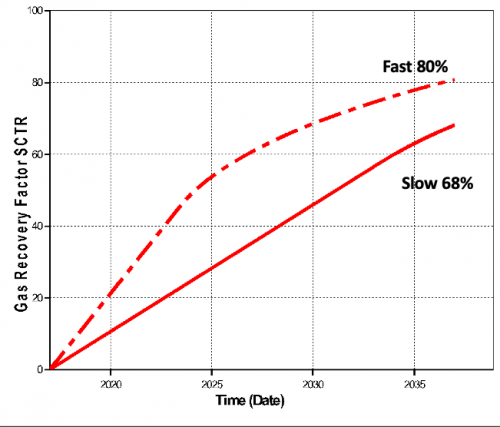
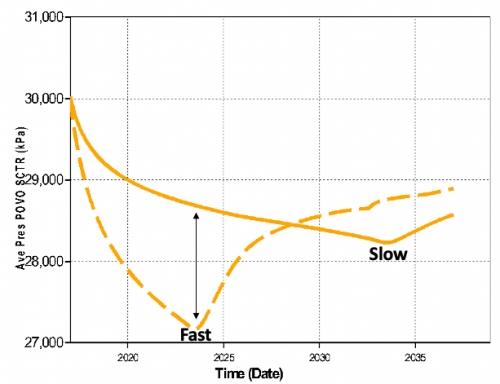
Gas Recovery

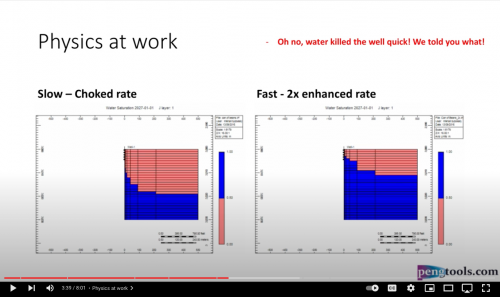
12% more recovery with the enhanced production over 20 years. Why?

Because of the pressure! The lower the reservoir pressure the more gas is produced before the water hits the perfs. It’s just physics!

Math and Physics

According to the Boyle's law (1662):

PV = constant

where P is pressure, V is volume.

In our case

PV = constant = P_1V_1 = P_2V_2=P_{res}V_{res}

The gas produced volume of the "Slow case"

V_1 = \frac{P_{res}V_{res}}{P_1}

The gas produced volume of the "Fast case"

V_2 = \frac{P_{res}V_{res}}{P_2}

And V₂ > V₁ because P₂ < P₁. The lower the P₂ gets over P₁ the higher the incremental recovery will be.

Summary

Produce gas reservoirs fast to increases recoveries.

If you have an aquifer you have to produce fast.

If you don’t have an aquifer…, so you don’t have water to complain.

Video

Watch our video explaining the gas reservoir production using the Can Of Beans (Gas) as an example

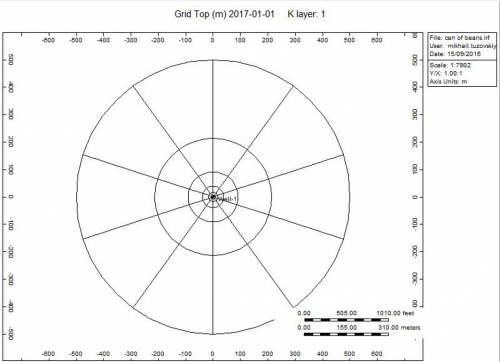
Model overview

Cylindrical grid (10x10x30)
re=500m, rw=0.1m, h=30m
kx=ky=5mD, kz/kx=0.1, phi=0.2
Pi=300bar, hres=3000m
Gas and water PVT model
SGgas=0.58
Aquifer at the bottom (CT infinite extent)
qgas_slow = 100 000 m3/d
qgas_fast = 200 000 m3/d

3D reservoir simulation software

ECLIPSE
tNavigator
CMG
Waiwera

References

Cite error: <ref> tag defined in <references> has group attribute "" which does not appear in prior text.

By Mikhail Tuzovskiy on 20230807172714

@@ Line 3: / Line 3: @@
 Before running any 3D reservoir simulator for a full scale field history matching or forecasts it is a good practice to make sure that the simulator is performing well on a simple benchmark tests with the well known analytical solutions.
-==Calculating well potential (well inflow performance)==
+By running those cases you could get ahead of the learning curve and gain confidence in your simulation results.
-If you eat the can of beans fast then the can doesn’t last as long as if you eat it slow, but you still eat the same amount of beans.
-Same logic is true for the gas reservoir with the bottom water.
+==Calculating well potential==
-There is a fixed volume of gas above the water.  When you remove the gas the water moves up. You can do it slow or fast but the volume of gas above the water is the same. The water level will raise Gravity stable as defined by Newton’s Law.
+Analytical equations are available to calculate the flow rate potential for unstimulated and stimulated wells.
+Steady state and pseudo steady state flow regimes are considered.
-==Simulation Runs==
+===Simulation Test Runs===
-Now let's attach the infinite aquifer to the can of gas and run scenarios:
+#Vertical well in a square drainage area pseudo steady state flow
-#Slow - choked gas rate
+#Vertical well in a square drainage area steady state flow
-#Fast - 2x enhanced gas rate
+#Fracture vertical well in a square drainage area pseudo steady state flow
-[[File:can_of_beans_Water_Saturation_slow.gif|Slow]]
+#Fractured vertical well in a square drainage area steady state flow
-[[File:can_of_beans_Water_Saturation_fast.gif|Fast]]
+#Horizontal well in a square drainage area pseudo steady state flow
+#Horizontal well in a square drainage area steady state flow
-Oh no, water killed the well quick in the "Fast" case! We told you what! Right, but … which case produced more gas?
+#Horizontal well with orthogonal fractures in a rectangular drainage area pseudo steady state flow
+#Horizontal well with orthogonal fractures in a rectangular drainage area steady state flow
 ==Gas Recovery==

Navigation menu

Navigation

Categories

Products