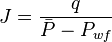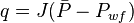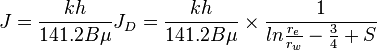Difference between revisions of "Productivity index"
From wiki.pengtools.com
(→Math & Physics) |
|||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
==Brief== | ==Brief== | ||
| − | [[Productivity index|J]] - well productivity index characterizes how much oil or water | + | [[Productivity index|J]] - well productivity index characterizes how much oil or water a well can produce per unit of the pressure drop. |
==Math & Physics== | ==Math & Physics== | ||
[[Productivity index|J]] is defined as follows: | [[Productivity index|J]] is defined as follows: | ||
:<math> {J} = \frac{q}{\bar{P} - P_{wf}} </math> | :<math> {J} = \frac{q}{\bar{P} - P_{wf}} </math> | ||
| + | Thus, rate could be calculated as: | ||
| + | :<math> {q} = {J}(\bar{P} - P_{wf})</math> | ||
From the [[Darcy's law]] for an unfractured well located in the center of a circular | From the [[Darcy's law]] for an unfractured well located in the center of a circular | ||
drainage area, the [[Productivity index|J]] in pseudo-steady state is: | drainage area, the [[Productivity index|J]] in pseudo-steady state is: | ||
:<math> {J} = \frac{kh}{141.2 B \mu} {J_D} = \frac{kh}{141.2 B \mu} \times \frac{1}{ln{\frac{r_e}{r_w}-\frac{3}{4}+S}} </math> | :<math> {J} = \frac{kh}{141.2 B \mu} {J_D} = \frac{kh}{141.2 B \mu} \times \frac{1}{ln{\frac{r_e}{r_w}-\frac{3}{4}+S}} </math> | ||
| − | |||
| − | |||
== Nomenclature == | == Nomenclature == | ||
:<math> B </math> = formation volume factor, bbl/stb | :<math> B </math> = formation volume factor, bbl/stb | ||
| + | :<math> J </math> = productivity index, stb/psia | ||
:<math> J_D </math> = dimensionless productivity index, dimensionless | :<math> J_D </math> = dimensionless productivity index, dimensionless | ||
:<math> kh</math> = permeability times thickness, md*ft | :<math> kh</math> = permeability times thickness, md*ft | ||
Latest revision as of 11:07, 14 June 2023
Brief
J - well productivity index characterizes how much oil or water a well can produce per unit of the pressure drop.
Math & Physics
J is defined as follows:
Thus, rate could be calculated as:
From the Darcy's law for an unfractured well located in the center of a circular drainage area, the J in pseudo-steady state is:
Nomenclature
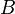= formation volume factor, bbl/stb
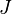= productivity index, stb/psia
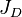= dimensionless productivity index, dimensionless
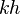= permeability times thickness, md*ft
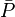= average reservoir pressure, psia
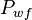= well flowing pressure, psia
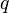= flowing rate, stb/d
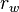= wellbore radius, ft
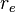= drainage radius, ft
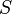= skin factor, dimensionless
Greek symbols
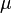= viscosity, cp
