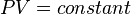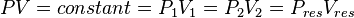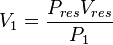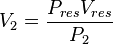Difference between revisions of "Can Of Beans (Gas)"
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style='text-align: | + | <div style='text-align: right;'>By Mikhail Tuzovskiy on {{REVISIONTIMESTAMP}}</div> |
==Brief == | ==Brief == | ||
| Line 10: | Line 10: | ||
What if you could increase the gas production and recover more gas instead? | What if you could increase the gas production and recover more gas instead? | ||
| − | '''Agarwal (1965)'''<ref name= Agarwal/> showed the | + | '''Agarwal (1965)'''<ref name= Agarwal/> showed the dependencies of production rates vs recoveries in gas reservoirs with water influx. |
This case study clearly demonstrates that gas recovery is '''increased''' with '''increasing''' the gas rate. | This case study clearly demonstrates that gas recovery is '''increased''' with '''increasing''' the gas rate. | ||
Latest revision as of 05:27, 3 January 2023
Contents
Brief
A case study on how to increase the gas recovery factor by increasing the gas production rates.
Have you ever heard that if you increase the choke size on a gas well, the well will "die" soon, because of the water? And gas recovery will go down too?
What if you could increase the gas production and recover more gas instead?
Agarwal (1965)[1] showed the dependencies of production rates vs recoveries in gas reservoirs with water influx.
This case study clearly demonstrates that gas recovery is increased with increasing the gas rate.
It is shown that enhanced well will add more reserves then non-enhanced well.
Case study is done using the simulation model assuring physics is well governed.
Can of beans analogy
If you eat the can of beans fast then the can doesn’t last as long as if you eat it slow, but you still eat the same amount of beans.
Same logic is true for the gas reservoir with the bottom water.
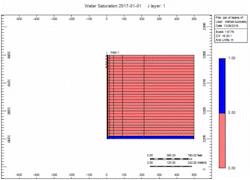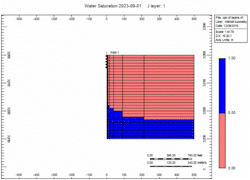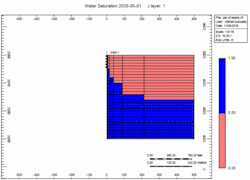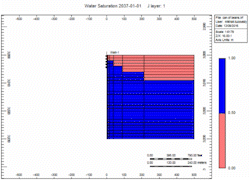
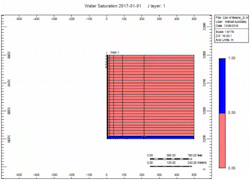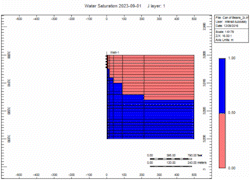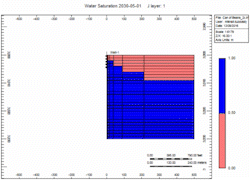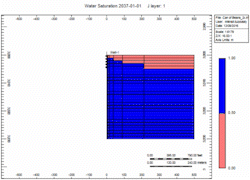
There is a fixed volume of gas above the water. When you remove the gas the water moves up. You can do it slow or fast but the volume of gas above the water is the same. The water level will raise Gravity stable as defined by Newton’s Law.
Simulation Runs
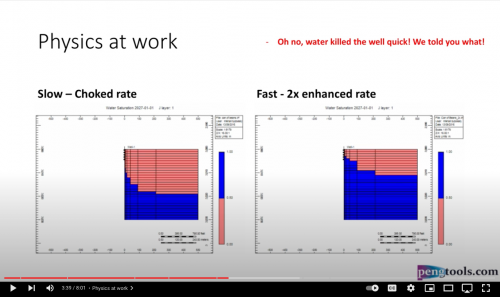
Now let's attach the infinite aquifer to the can of gas and run scenarios:
- Slow - choked gas rate
- Fast - 2x enhanced gas rate
Oh no, water killed the well quick in the "Fast" case! We told you what! Right, but … which case produced more gas?
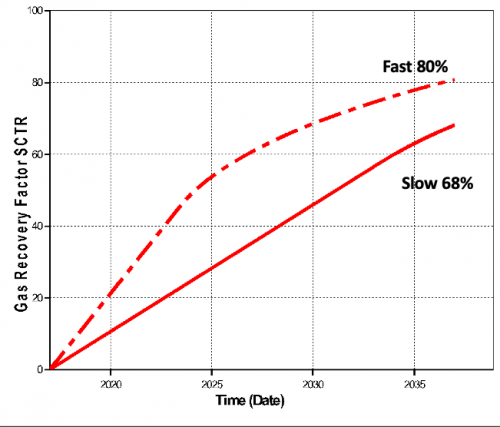
Gas Recovery
12% more recovery with the enhanced production over 20 years. Why?
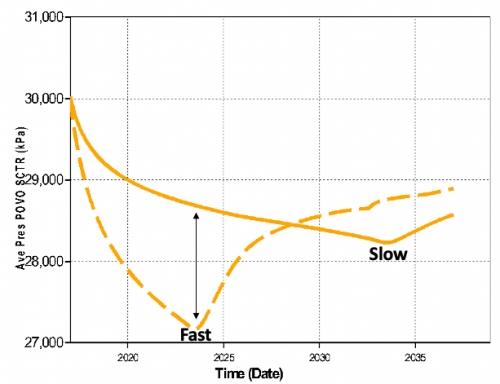
Because of the pressure! The lower the reservoir pressure the more gas is produced before the water hits the perfs. It’s just physics!
Math and Physics
According to the Boyle's law (1662):
where P is pressure, V is volume.
In our case
The gas produced volume of the "Slow case"
The gas produced volume of the "Fast case"
And V2 > V1 because P2 < P1. The lower the P2 gets over P1 the higher the incremental recovery will be.
Summary
Produce gas reservoirs fast to increases recoveries.
If you have an aquifer you have to produce fast.
If you don’t have an aquifer…, so you don’t have water to complain.
Video
Watch our video explaining the gas reservoir production using the Can Of Beans (Gas) as an example
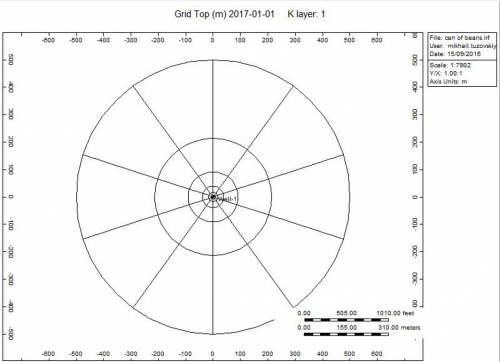
Model overview
- Cylindrical grid (10x10x30)
- re=500m, rw=0.1m, h=30m
- kx=ky=5mD, kz/kx=0.1, phi=0.2
- Pi=300bar, hres=3000m
- Gas and water PVT model
- SGgas=0.58
- Aquifer at the bottom (CT infinite extent)
- qgas_slow = 100 000 m3/d
- qgas_fast = 200 000 m3/d
See also
References
- ↑
Agarwal, R.G.; Al-Hussainy, R.; Ramey, Jr., H.J. (1965). "The Importance of Water Influx in Gas Reservoirs"
 (SPE-1244-PA). Journal of Petroleum Technology.
(SPE-1244-PA). Journal of Petroleum Technology.