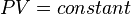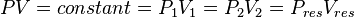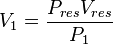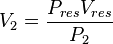Difference between revisions of "Can Of Beans (Gas)"

From wiki.pengtools.com
Jump to: navigation, search
(→‎Can Of Beans (Gas))
 
(72 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
==Can Of Beans (Gas) ==
+
<div style='text-align: right;'>By Mikhail Tuzovskiy on {{REVISIONTIMESTAMP}}</div>
−
[[File:Can Of Beans (Gas).png|thumb|right|400px| Case Study]]
 
  
−
A case study on how to increase the gas recovery factor by increasing the production rates.
+
==Brief ==
 +
[[File:Can Of Beans (Gas).png|thumb|right|400px| If you eat the can of beans fast then the can doesn’t last as long as if you eat it slow, but you still eat the same amount of beans.]]
  
−
{{Quote| text = If you eat the can of beans fast then the can doesn’t last as long as if you eat it slow, but you still eat the same amount of beans. | source = Don Wolcott}}
+
A case study on how to increase the gas recovery factor by increasing the gas production rates.
  
−
==Why a Case Study?==
+
Have you ever heard that if you increase the choke size on a gas well, the well will "die" soon, because of the water? And gas recovery will go down too?
  
 +
What if you could increase the gas production and recover more gas instead?
  
−
[[Well Nodal Analysis]] is the fundamental [[Petroleum Engineering|petroleum engineering]] technique published in '''1979''' by Joe Mach <ref name=JoeMach/>.  
+
'''Agarwal (1965)'''<ref name= Agarwal/> showed the dependencies of production rates vs recoveries in gas reservoirs with water influx.
  
−
==The Power of Well Nodal Analysis==
+
This case study clearly demonstrates that gas recovery is '''increased''' with '''increasing''' the gas rate.
−
[[File:Location of various nodes.png|thumb|right|400px| Location of various nodes <ref name=JoeMach/>]]
 
  
−
[[Well Nodal Analysis]] is the cornerstone of [[Petroleum Engineering| petroleum engineering]]. It allows to:
+
It is shown that enhanced well will add more reserves then non-enhanced well.
  
−
==Typical Applications==
+
Case study is done using the simulation model assuring physics is well governed.
 +
 
 +
==Can of beans analogy==
 +
If you eat the can of beans fast then the can doesn’t last as long as if you eat it slow, but you still eat the same amount of beans.
 +
 
 +
Same logic is true for the gas reservoir with the bottom water.
 +
 
 +
There is a fixed volume of gas above the water.  When you remove the gas the water moves up. You can do it slow or fast but the volume of gas above the water is the same. The water level will raise Gravity stable as defined by Newton’s Law.
 +
 
 +
==Simulation Runs==
 +
 
 +
Now let's attach the infinite aquifer to the can of gas and run scenarios:
 +
#Slow - choked gas rate
 +
#Fast - 2x enhanced gas rate
 +
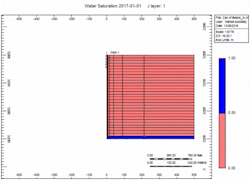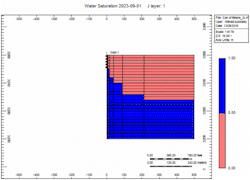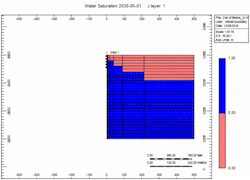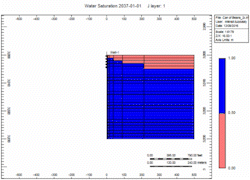
[[File:can_of_beans_Water_Saturation_slow.gif|Slow]]
 +
[[File:can_of_beans_Water_Saturation_fast.gif|Fast]]
 +
 
 +
Oh no, water killed the well quick in the "Fast" case! We told you what! Right, but … which case produced more gas?
 +
 
 +
==Gas Recovery==
 +
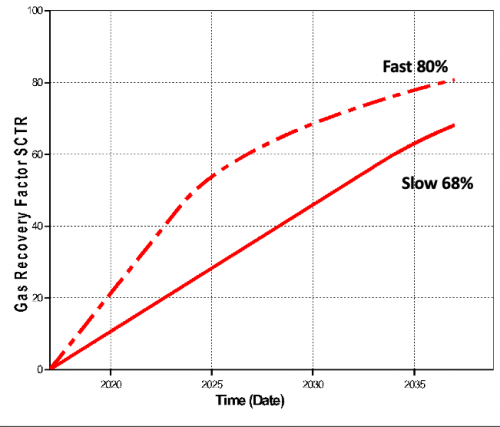
[[File:Can of Beans (Gas) recovery.png|500px|Gas Recovery Results]]
 +
 
 +
12% more recovery with the enhanced production over 20 years. Why?
 +
 
 +
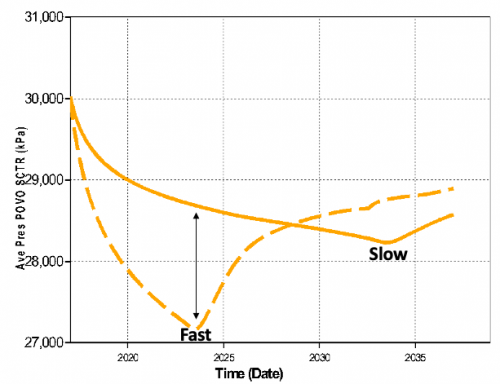
Because of the pressure! The lower the reservoir pressure the more gas is produced before the water hits the perfs. It’s just physics!
 +
 
 +
[[File:Can of Beans (Gas) pressure.png|500px|Reservoir Pressure]]
  
 
==Math and Physics==
 
==Math and Physics==
−
[[Well Nodal Analysis]] is done on a pressure vs rate plot. [[IPR]] and [[VLP]] curves intersect at well operating point.
+
According to the '''Boyle's law (1662)''':
 +
 
 +
:<math> PV = constant </math>
  
−
Well [[IPR]] curve: [[Darcy's law]], [[Vogel's IPR]], [[Composite IPR]].
+
where P is pressure, V is volume.
  
−
Well [[VLP]] curve: [[Hagedorn and Brown]] multiphase flow correlation
+
In our case
  
−
==Well Nodal Analysis Example==
+
:<math> PV = constant = P_1V_1 = P_2V_2=P_{res}V_{res}</math>
−
Given data<ref name=JoeMach/>:
 
−
SG<sub>g</sub>=0.65, SG<sub>o</sub>=35 API, P<sub>r</sub>=2200 psi, P<sub>b</sub>=1800 psi, T<sub>r</sub>=140 F, depth = 5000ft, tubing size = 2 3/8 in OD, GOR=400 scf/stb, WOR=0
 
−
Productivity index J = 1 bbl/d/psi
 
  
−
It's required to find the well flowing rate at the wellhead pressure of 230 psi. Surface flow line and separator are not in question.
+
The gas produced volume of the "Slow case"
−
===Solution at bottom of well ===
+
:<math> V_1 = \frac{P_{res}V_{res}}{P_1}</math>
−
In order to solve for the flow rate at bottomhole (node position 6), the entire system  is divided into two components, the reservoir or well capability component, [[IPR]] and the piping system component, [[VLP]] <ref name= KermitBrown1984/>.
 
  
−
:First, [[Vogel's IPR | Vogel's equation]] is used to calculate the [[IPR]] curve. The AOF = 1400 bbl/d
+
The gas produced volume of the "Fast case"
 +
:<math> V_2 = \frac{P_{res}V_{res}}{P_2}</math>
  
−
<table border="1" cellpadding="3" cellspacing="1">
+
And V<sub>2</sub> > V<sub>1</sub> because P<sub>2</sub> < P<sub>1</sub>. The lower the P<sub>2</sub> gets over P<sub>1</sub> the higher the incremental recovery will be.
−
<tr><th>Rate, bbl/d</th><th>Pwf, psi</th></tr>
 
−
<tr><td>0</td><td>2200</td></tr>
 
−
<tr><td>200</td><td>2000</td></tr>
 
−
<tr><td>400</td><td>1800</td></tr>
 
−
<tr><td>600</td><td>1590</td></tr>
 
−
<tr><td>800</td><td>1350</td></tr>
 
−
<tr><td>1000</td><td>1067</td></tr>
 
−
<tr><td>1400</td><td>0</td></tr>
 
−
</table>
 
  
 +
==Summary==
 +
Produce gas reservoirs fast to increases recoveries.
  
−
:Second, [[Hagedorn and Brown]] multiphase flow correlation is used to calculate the required tubing intake pressures at the given wellhead pressure, [[VLP]] curve.
+
If you have an aquifer you have to produce fast.
  
−
<table border="1" cellpadding="3" cellspacing="1">
+
If you don’t have an aquifer…, so you don’t have water to complain.
−
<tr><th>Rate, bbl/d</th><th>Pwf, psi</th></tr>
 
−
<tr><td>0</td><td>1929</td></tr>
 
−
<tr><td>200</td><td>1065</td></tr>
 
−
<tr><td>400</td><td>1125</td></tr>
 
−
<tr><td>600</td><td>1181</td></tr>
 
−
<tr><td>800</td><td>1235</td></tr>
 
−
<tr><td>1000</td><td>1289</td></tr>
 
−
<tr><td>1400</td><td>1399</td></tr>
 
−
</table>
 
  
 +
==Video==
 +
Watch our video explaining the gas reservoir production using the [[Can Of Beans (Gas)]] as an example
  
−
:Third, [[IPR]] and [[VLP]] curves are plotted on the pressure vs rate plot. The intersection of these two curves shows the flow rate to be 872 bbl/d.
+
[[File:Can of Beans (Gas) video.png|500px|https://youtu.be/RPrBpKXpcZk | Watch on youtube]]
  
−
[[File:Well Nodal Analysis Example.png | link=https://www.pengtools.com/pqPlot?paramsToken=7db370789c234c0949337f8b1978fa3c | Solution at Bottom of Well]]
+
==Model overview==
 +
[[File:Can of Beans (Gas) model.png|500px|Simulation model]]
  
−
{{Quote| text = This is "the rate" possible for this system. It is not a maximum, minimum, or optimum but is the rate at which this well will produce for the piping system installed. The rate can be changed only by changing something in the system - that is, pipe sizes, choke or by shifting the [[IPR]] curve through simulation treatment. | source = Kermit Brown et al <ref name= KermitBrown1984/>}}
+
*Cylindrical grid (10x10x30)
 +
*re=500m, rw=0.1m, h=30m
 +
*kx=ky=5mD, kz/kx=0.1, phi=0.2
 +
*Pi=300bar, hres=3000m
 +
*Gas and water PVT model
 +
*SGgas=0.58
 +
*Aquifer at the bottom (CT infinite extent)
 +
*qgas_slow = 100 000 m3/d
 +
*qgas_fast = 200 000 m3/d
  
 
== See also ==
 
== See also ==
 
*[[Petroleum Engineering]]
 
*[[Petroleum Engineering]]
 
*[[Hydraulic fracturing]]
 
*[[Hydraulic fracturing]]
 +
*[[29+ reasons why you can not increase the production]]
  
 
== References ==
 
== References ==
 
<references>
 
<references>
  
−
<ref name= JoeMach>
+
<ref name= Agarwal>
−
{{cite journal
 
−
|last1= Mach |first1=Joe
 
−
|last2= Proano |first2=Eduardo
 
−
|last3= Brown |first3=Kermit E.
 
−
|title=A Nodal Approach For Applying Systems Analysis To The Flowing And Artificial Lift Oil Or Gas Well
 
−
|date=1979
 
−
|publisher=Society of Petroleum Engineers
 
−
|number=SPE-8025-MS
 
−
|url=https://www.onepetro.org/general/SPE-8025-MS
 
−
|url-access=registration
 
−
}}</ref>
 
−
 
 
−
<ref name=Legends>
 
 
{{cite journal
 
{{cite journal
−
  |last1= JPT |first1=staff
+
  |last1= Agarwal |first1=R.G.
−
  |title=Legends of Production and Operation
+
  |last2= Al-Hussainy |first2=R.
−
  |date=2009
+
  |last3= Ramey, Jr. |first3=H.J.
−
  |publisher=Society of Petroleum Engineers
+
  |title=The Importance of Water Influx in Gas Reservoirs
−
  |journal=Journal of Petroleum Technology
+
|date=1965
−
  |number=SPE-1209-0033-JPT
+
  |publisher=Journal of Petroleum Technology
−
  |url=https://www.onepetro.org/journal-paper/SPE-1209-0033-JPT
+
  |number=SPE-1244-PA
 +
  |url=https://onepetro.org/JPT/article/17/11/1336/162535/The-Importance-of-Water-Influx-in-Gas-Reservoirs
 
  |url-access=registration  
 
  |url-access=registration  
−
 
−
}}</ref>
 
−
 
−
<ref name= KermitBrown1984 >{{cite book
 
−
|last1= Brown |first1= Kermit
 
−
|title=The Technology of Artificial Lift Methods. Volume 4. Production Optimization of Oil and Gas Wells by Nodal System Analysis
 
−
|publisher=PennWellBookss
 
−
|date=1984
 
−
|place=Tulsa, Oklahoma
 
 
}}</ref>
 
}}</ref>
  

Latest revision as of 05:27, 3 January 2023

By Mikhail Tuzovskiy on 20230103052733

Brief

If you eat the can of beans fast then the can doesn’t last as long as if you eat it slow, but you still eat the same amount of beans.

A case study on how to increase the gas recovery factor by increasing the gas production rates.

Have you ever heard that if you increase the choke size on a gas well, the well will "die" soon, because of the water? And gas recovery will go down too?

What if you could increase the gas production and recover more gas instead?

Agarwal (1965)[1] showed the dependencies of production rates vs recoveries in gas reservoirs with water influx.

This case study clearly demonstrates that gas recovery is increased with increasing the gas rate.

It is shown that enhanced well will add more reserves then non-enhanced well.

Case study is done using the simulation model assuring physics is well governed.

Can of beans analogy

If you eat the can of beans fast then the can doesn’t last as long as if you eat it slow, but you still eat the same amount of beans.

Same logic is true for the gas reservoir with the bottom water.

There is a fixed volume of gas above the water.  When you remove the gas the water moves up. You can do it slow or fast but the volume of gas above the water is the same. The water level will raise Gravity stable as defined by Newton’s Law.

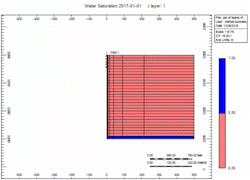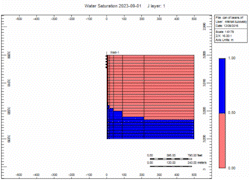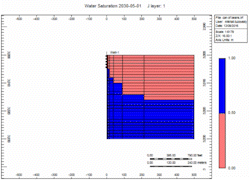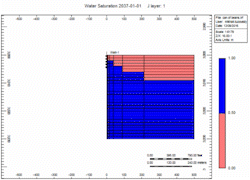
Simulation Runs

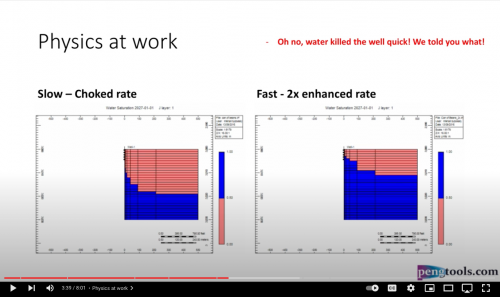
Now let's attach the infinite aquifer to the can of gas and run scenarios:

  1. Slow - choked gas rate
  2. Fast - 2x enhanced gas rate

Slow Fast

Oh no, water killed the well quick in the "Fast" case! We told you what! Right, but … which case produced more gas?

Gas Recovery

Gas Recovery Results

12% more recovery with the enhanced production over 20 years. Why?

Because of the pressure! The lower the reservoir pressure the more gas is produced before the water hits the perfs. It’s just physics!

Reservoir Pressure

Math and Physics

According to the Boyle's law (1662):

PV = constant

where P is pressure, V is volume.

In our case

PV = constant = P_1V_1 = P_2V_2=P_{res}V_{res}

The gas produced volume of the "Slow case"

V_1 = \frac{P_{res}V_{res}}{P_1}

The gas produced volume of the "Fast case"

V_2 = \frac{P_{res}V_{res}}{P_2}

And V2 > V1 because P2 < P1. The lower the P2 gets over P1 the higher the incremental recovery will be.

Summary

Produce gas reservoirs fast to increases recoveries.

If you have an aquifer you have to produce fast.

If you don’t have an aquifer…, so you don’t have water to complain.

Video

Watch our video explaining the gas reservoir production using the Can Of Beans (Gas) as an example

Watch on youtube

Model overview

Simulation model

  • Cylindrical grid (10x10x30)
  • re=500m, rw=0.1m, h=30m
  • kx=ky=5mD, kz/kx=0.1, phi=0.2
  • Pi=300bar, hres=3000m
  • Gas and water PVT model
  • SGgas=0.58
  • Aquifer at the bottom (CT infinite extent)
  • qgas_slow = 100 000 m3/d
  • qgas_fast = 200 000 m3/d

See also

References

  1. ↑ Agarwal, R.G.; Al-Hussainy, R.; Ramey, Jr., H.J. (1965). "The Importance of Water Influx in Gas Reservoirs"Free registration required (SPE-1244-PA). Journal of Petroleum Technology. 
Retrieved from "https://wiki.pengtools.com/index.php?title=Can_Of_Beans_(Gas)&oldid=7602"