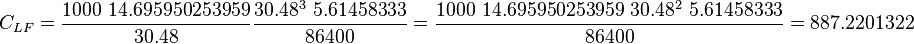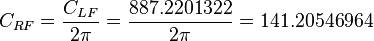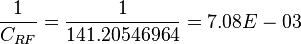Difference between revisions of "141.2 derivation"
From wiki.pengtools.com
(→Math and Physics) |
|||
| (13 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
'''141.2''' is the well know constant which is used for converting from the [[Darcy's law]] units to the field units in the well's inflow equations. | '''141.2''' is the well know constant which is used for converting from the [[Darcy's law]] units to the field units in the well's inflow equations. | ||
| − | For example Darcy's law for the single-phase flow is as follows<ref name=KermitBrown/>: | + | For example [[Darcy's law]] for the single-phase flow is as follows<ref name=KermitBrown/>: |
:<math> q_o = \frac{1}{141.2} \times \frac{k_oh}{B_o\mu_o} \times \Delta P \times J_D = 7.08 \times 10^-3 \times \frac{k_oh}{B_o\mu_o} \times \Delta P \times J_D</math> | :<math> q_o = \frac{1}{141.2} \times \frac{k_oh}{B_o\mu_o} \times \Delta P \times J_D = 7.08 \times 10^-3 \times \frac{k_oh}{B_o\mu_o} \times \Delta P \times J_D</math> | ||
| Line 22: | Line 22: | ||
Converting to the field units: | Converting to the field units: | ||
| − | :<math> \frac{[cm^3] \frac{[ft^3]}{[30.48^3 cm^3]} \frac{[bbl]}{[5.61458333 ft^3]} }{[sec] \frac{[day]}{[86400 sec]}} = - \frac{[D] \frac{[1000 mD]}{[D]}[cm^2] \frac{[ft^2]}{[30.48^2 cm]}}{[cP]} \frac{[atm] \frac{[14.695950253959 psia]}{[atm]}}{[cm] \frac{[ft]}{[30.48 cm]}}</math> | + | :<math> \frac{[cm^3] \frac{[ft^3]}{[30.48^3 cm^3]} \frac{[bbl]}{[5.61458333 ft^3]} }{[sec] \frac{[day]}{[86400 sec]}} = - \frac{[D] \frac{[1000 mD]}{[D]}[cm^2] \frac{[ft^2]}{[30.48^2 cm^2]}}{[cP]} \frac{[atm] \frac{[14.695950253959 psia]}{[atm]}}{[cm] \frac{[ft]}{[30.48 cm]}}</math> |
So: | So: | ||
| Line 43: | Line 43: | ||
:<math> \frac{1}{C_{RF}} = \frac{1}{141.20546964} = 7.08E-03 </math> | :<math> \frac{1}{C_{RF}} = \frac{1}{141.20546964} = 7.08E-03 </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Nomenclature == | == Nomenclature == | ||
| − | :<math> | + | :<math> A </math> = [[Darcy's law]] cross-sectional area, cm<sup>2</sup> |
:<math> B_o </math> = oil formation volume factor, bbl/stb | :<math> B_o </math> = oil formation volume factor, bbl/stb | ||
| + | :<math> C_{LF} </math> = linear flow units conversion constant | ||
| + | :<math> C_{RF} </math> = radial flow units conversion constant | ||
:<math> h</math> = effective feet of oil pay, ft | :<math> h</math> = effective feet of oil pay, ft | ||
:<math> J_D </math> = dimensionless productivity index, dimensionless | :<math> J_D </math> = dimensionless productivity index, dimensionless | ||
| Line 67: | Line 64: | ||
:<math> \mu </math> = [[Darcy's law]] oil viscosity, cp | :<math> \mu </math> = [[Darcy's law]] oil viscosity, cp | ||
:<math> \mu_o </math> = oil viscosity, cp | :<math> \mu_o </math> = oil viscosity, cp | ||
| + | |||
| + | ==See Also== | ||
| + | [[Darcy's law]]<BR/> | ||
| + | [[141.2 derivation]]<BR/> | ||
| + | [[18.41 derivation]] | ||
==References== | ==References== | ||
| Line 85: | Line 87: | ||
[[Category:Technology]] | [[Category:Technology]] | ||
| + | |||
| + | {{#seo: | ||
| + | |title=141.2 derivation | ||
| + | |titlemode= replace | ||
| + | |keywords=141.2 derivation | ||
| + | |description=141.2 derivation is the well know constant which is used for converting from the Darcy's law units to the field units in the well's inflow equations. | ||
| + | }} | ||
| + | <div style='text-align: right;'>By Mikhail Tuzovskiy on {{REVISIONTIMESTAMP}}</div> | ||
Latest revision as of 12:33, 12 July 2023
Brief
141.2 is the well know constant which is used for converting from the Darcy's law units to the field units in the well's inflow equations.
For example Darcy's law for the single-phase flow is as follows[1]:
The derivation of the 141.2 constant is given below.
Math and Physics
In Darcy's units:
Converting to the field units:
So:
And:
where
For the radial flow:
One can be familiar with the inverse of the 141.2 constant:
Nomenclature
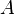 = Darcy's law cross-sectional area, cm2
= Darcy's law cross-sectional area, cm2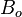 = oil formation volume factor, bbl/stb
= oil formation volume factor, bbl/stb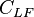 = linear flow units conversion constant
= linear flow units conversion constant 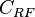 = radial flow units conversion constant
= radial flow units conversion constant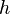 = effective feet of oil pay, ft
= effective feet of oil pay, ft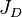 = dimensionless productivity index, dimensionless
= dimensionless productivity index, dimensionless = Darcy's law permeability, d
= Darcy's law permeability, d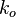 = effective permeability to oil, md
= effective permeability to oil, md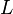 = Darcy's law length, cm
= Darcy's law length, cm = Darcy's law pressure, atm
= Darcy's law pressure, atm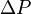 = drawdown, psia
= drawdown, psia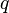 = Darcy's law flow rate, cm3/sec
= Darcy's law flow rate, cm3/sec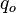 = oil flow rate, stb/d
= oil flow rate, stb/d
Greek symbols
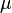 = Darcy's law oil viscosity, cp
= Darcy's law oil viscosity, cp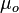 = oil viscosity, cp
= oil viscosity, cp
See Also
Darcy's law
141.2 derivation
18.41 derivation
References
- ↑ Brown, Kermit (1984). The Technology of Artificial Lift Methods. Volume 4. Production Optimization of Oil and Gas Wells by Nodal System Analysis. 4. Tulsa, Oklahoma: PennWellBooks.
By Mikhail Tuzovskiy on 20230712123301
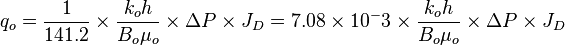
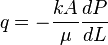
![\frac{[cm^3]}{[sec]} = - \frac{[D][cm^2]}{[cP]} \frac{[atm]}{[cm]}](/images/math/5/5/5/555b9dc7f65e6db7f1cd05153aaae770.png)
![\frac{[cm^3] \frac{[ft^3]}{[30.48^3 cm^3]} \frac{[bbl]}{[5.61458333 ft^3]} }{[sec] \frac{[day]}{[86400 sec]}} = - \frac{[D] \frac{[1000 mD]}{[D]}[cm^2] \frac{[ft^2]}{[30.48^2 cm^2]}}{[cP]} \frac{[atm] \frac{[14.695950253959 psia]}{[atm]}}{[cm] \frac{[ft]}{[30.48 cm]}}](/images/math/a/e/f/aef6ab96a93f70f9312ea71cca7aeb57.png)
![\frac{[bbl]}{[day]} \frac{86400}{30.48^3\ 5.61458333} = - \frac{[mD][ft^2]}{[cP]} \frac{[psia]}{[ft]} \frac{1000\ 14.695950253959}{30.48}](/images/math/9/a/b/9abe955d3e8338add13d1fe96e9fd738.png)
![\frac{[bbl]}{[day]} = - C_{LF} \frac{[mD][ft^2]}{[cP]} \frac{[psia]}{[ft]}](/images/math/d/d/4/dd4c5bbb71e5c38a6ae238f62d56d9ea.png)