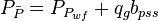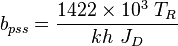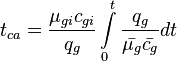Difference between revisions of "Gas Flowing Material Balance"
(→Workflow) |
|||
| (87 intermediate revisions by 2 users not shown) | |||
| Line 2: | Line 2: | ||
== Brief == | == Brief == | ||
| − | [[Gas Flowing Material Balance]] is the advanced engineering technique | + | [[Gas Flowing Material Balance]] '''(Gas FMB)''' is the advanced engineering technique published in '''1998''' by Louis Mattar <ref name=Mattar1998/>. |
| − | [[Gas Flowing Material Balance]] is applied | + | [[Gas Flowing Material Balance]] is applied to determine: |
| + | * [[Reservoirs]] GIIP calculation | ||
| + | * [[Reservoirs]] [[EUR]] calculation | ||
| + | * [[Well]]'s [[EUR]] and [[JD]] | ||
| − | The interpretation technique is fitting the data points with the straight | + | [[Gas Flowing Material Balance]] uses readily available [[Well]] flowing data: production rate and tubing head pressure. |
| + | |||
| + | The interpretation technique is fitting the data points with the straight lines to calculate GIIP and [[JD]]. | ||
| + | |||
| + | [[File:FMB.png|link=https://ep.pengtools.com/matbal/flowing-material-balance/gas]] | ||
| + | |||
| + | <center>[[Gas Flowing Material Balance]] in the [https://ep.pengtools.com/matbal/flowing-material-balance/gas E&P Portal]</center> | ||
== Math & Physics == | == Math & Physics == | ||
| Line 24: | Line 33: | ||
==Discussion== | ==Discussion== | ||
| − | well | + | [[Gas Flowing Material Balance]] can be applied to: |
| + | *single well | ||
| + | *multiple wells producing from the same [[Reservoirs| Reservoir]]. | ||
| + | |||
| + | The X axis on the [[Gas Flowing Material Balance]] Plot can be selected as: | ||
| + | *[[Well]] cumulative | ||
| + | *[[Reservoirs| Reservoir]] cumulative | ||
| + | |||
| + | '''Example 1. Multiple wells producing from the same Reservoir. X axis - Wells cumulative''' | ||
| + | [[File:FMBex1.png|link=https://ep.pengtools.com/matbal/flowing-material-balance/gas]] | ||
| + | '''Example 2. Multiple wells producing from the same Reservoir. X axis - Reservoir cumulative''' | ||
| + | [[File:FMBex2.png|link=https://ep.pengtools.com/matbal/flowing-material-balance/gas]] | ||
| + | '''Example 3. Shifted Model Start (to account for gas injection)''' | ||
| + | [[File:FMBex3.png|link=https://ep.pengtools.com/matbal/flowing-material-balance/gas]] | ||
==Workflow== | ==Workflow== | ||
| + | # Upload the data required | ||
| + | # Open the [[Gas Flowing Material Balance]] tool [https://ep.pengtools.com/matbal/flowing-material-balance/gas here] | ||
# Calculate the red <math> \frac{P}{z}</math> line: | # Calculate the red <math> \frac{P}{z}</math> line: | ||
## Given the GIIP | ## Given the GIIP | ||
| − | ## Calculate <math> \frac{P}{z}=\frac{P_i}{z_i} \left (1- \frac{G_p}{GIIP}\right )</math> | + | ## Calculate the <math> \frac{P}{z}=\frac{P_i}{z_i} \left (1- \frac{G_p}{GIIP}\right )</math> |
# Calculate the orange <math> \frac{\bar{P}}{z}</math> curve: | # Calculate the orange <math> \frac{\bar{P}}{z}</math> curve: | ||
## Given the flowing wellhead pressures, calculate the flowing bottomhole pressures, <math>P_{wf}</math> | ## Given the flowing wellhead pressures, calculate the flowing bottomhole pressures, <math>P_{wf}</math> | ||
| Line 42: | Line 66: | ||
# Change the red <math> \frac{P}{z}</math> line to match the orange <math> \frac{\bar{P}}{z}</math> curve | # Change the red <math> \frac{P}{z}</math> line to match the orange <math> \frac{\bar{P}}{z}</math> curve | ||
## Change the GIIP | ## Change the GIIP | ||
| − | ## Change the <math> \frac{P}{z}</math> | + | ## Change the intitial <math> \frac{P}{z}</math> |
# Change the flat [[JD]] gray line to match the changing [[JD]] gray line | # Change the flat [[JD]] gray line to match the changing [[JD]] gray line | ||
| − | # Save the [[Gas Flowing Material Balance]] model | + | # Save the [[Gas Flowing Material Balance| FMB]] model |
# Move to the next well | # Move to the next well | ||
| − | ===Extra Plot to find b<sub> | + | ===Extra Plot to find b<sub>pss</sub>=== |
| − | Calculate initial pseudopressure, <math>P_{Pi}</math> | + | #Calculate the initial pseudopressure, <math>P_{Pi}</math> |
| − | Calculate material balance pseudo-time, <math>t_{ca}</math> | + | #Calculate the material balance pseudo-time, <math>t_{ca}</math> |
| − | Plot <math>\frac{P_{P_i}-P_{P_{wf}}}{ | + | #Plot <math>\frac{P_{P_i}-P_{P_{wf}}}{q_g}</math> versus <math>t_{ca}</math> |
| − | + | #The intercept with the Y axis gives <math>b_{pss}</math> and <math>J_D</math> | |
| − | + | == Data required == | |
| − | + | ||
| − | + | {{Data required for Gas Flowing Material Balance}} | |
| − | |||
== Nomenclature == | == Nomenclature == | ||
| − | :<math> | + | :<math> b_{pss} </math> = reservoir constant, inverse to productivity index, psia<sup>2</sup>/cP/MMscfd |
| − | + | :<math> c </math> = compressibility, psia<sup>-1</sup> | |
| − | + | :<math> GIIP </math> = gas initially in place, MMscf | |
| − | + | :<math> G_p </math> = cumulative gas produced, MMscf | |
| − | :<math> | + | :<math> J </math> = gas productivity index, MMscfd/(psia<sup>2</sup>/cP) |
| − | + | :<math> J_D </math> = dimensionless productivity index, dimensionless | |
| − | :<math> | + | :<math> kh</math> = permeability times thickness, md*ft |
| − | :<math> | + | :<math> P </math> = pressure, psia |
| − | + | :<math> \bar{P} </math> = average reservoir pressure, psia | |
| − | :<math> | + | :<math> P_P </math> = pseudopressure, psia<sup>2</sup>/cP |
| − | + | :<math> q_g </math> = gas rate, MMscfd | |
| − | :<math> | + | :<math> t </math> = time, day |
| − | + | :<math> t_{ca} </math> = material balance pseudotime for gas, day | |
| − | :<math> | + | :<math> T </math> = temperature, °R |
| − | :<math> | ||
| − | :<math> | ||
| − | :<math> | ||
| − | :<math> | ||
| − | :<math> | ||
| − | :<math> | ||
| − | |||
| − | :<math> T </math> = temperature, °R | ||
| − | |||
| − | |||
:<math> z </math> = gas compressibility factor, dimensionless | :<math> z </math> = gas compressibility factor, dimensionless | ||
===Greek symbols=== | ===Greek symbols=== | ||
| − | |||
:<math> \mu </math> = viscosity, cp | :<math> \mu </math> = viscosity, cp | ||
| − | |||
| − | |||
| − | |||
| − | |||
===Subscripts=== | ===Subscripts=== | ||
:g = gas<BR/> | :g = gas<BR/> | ||
| − | : | + | :i = initial<BR/> |
| − | |||
| − | |||
| − | |||
:R = °R<BR/> | :R = °R<BR/> | ||
| − | : | + | :wf = well flowing <BR/> |
| − | |||
| − | |||
== References == | == References == | ||
<references> | <references> | ||
| + | <ref name=Mattar1998>{{cite journal | ||
| + | |last1=Mattar|first1=L. | ||
| + | |last2= McNeil |first2=R. | ||
| + | |title=The "Flowing" Gas Material Balance | ||
| + | |publisher=Petroleum Society of Canada | ||
| + | |journal=Journal of Canadian Petroleum Technology | ||
| + | |date=1998 | ||
| + | |url=https://ihsmarkit.com/pdf/flowing-gas-material-bal-paper_228615110913049832.pdf | ||
| + | }}</ref> | ||
<ref name=Mattar2005>{{cite journal | <ref name=Mattar2005>{{cite journal | ||
| Line 124: | Line 136: | ||
[[Category:E&P Portal]] | [[Category:E&P Portal]] | ||
| + | |||
| + | {{#seo: | ||
| + | |title=Gas Flowing Material Balance for GIIP calculation | ||
| + | |titlemode= replace | ||
| + | |keywords=giip calculation, reservoir engineering, flowing material balance, petroleum engineering, equation | ||
| + | |description=Gas Flowing Material Balance is the advanced engineering technique applied to calculate reservoirs and wells GIIP and productivity index. | ||
| + | }} | ||
Latest revision as of 18:00, 3 November 2018
Contents
Brief
Gas Flowing Material Balance (Gas FMB) is the advanced engineering technique published in 1998 by Louis Mattar [1].
Gas Flowing Material Balance is applied to determine:
- Reservoirs GIIP calculation
- Reservoirs EUR calculation
- Well's EUR and JD
Gas Flowing Material Balance uses readily available Well flowing data: production rate and tubing head pressure.
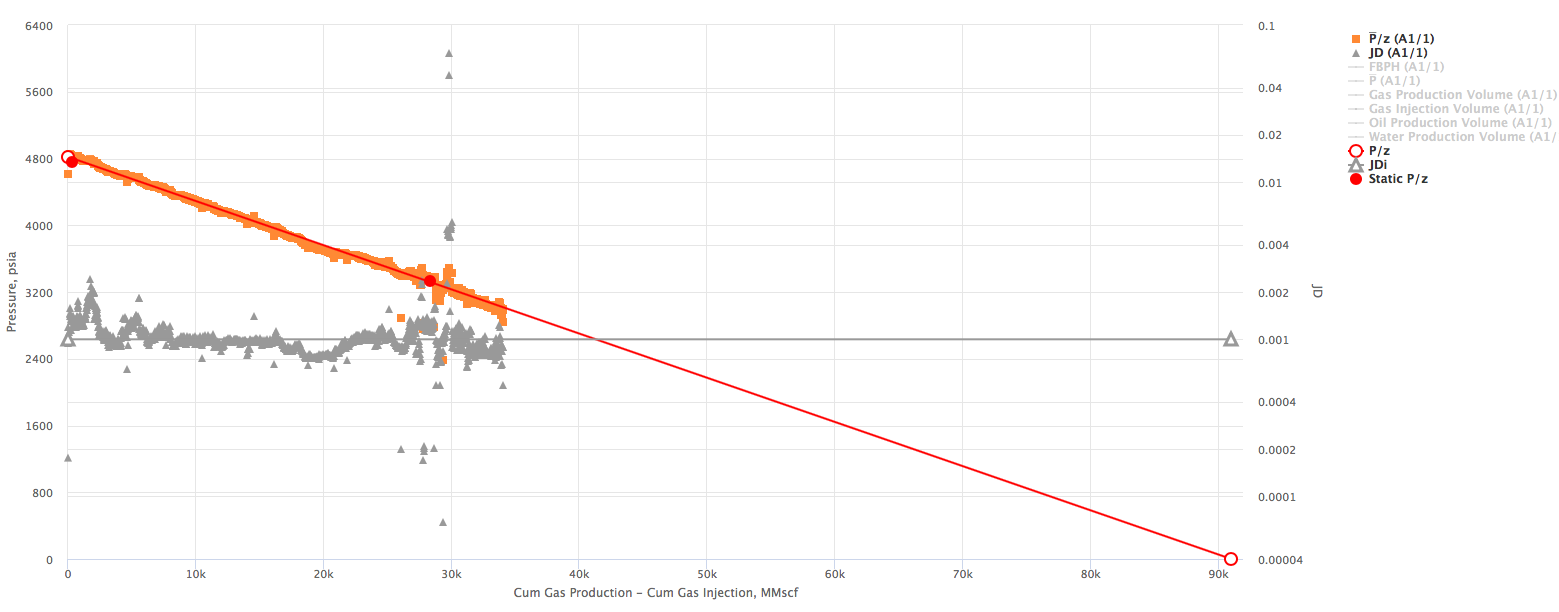
The interpretation technique is fitting the data points with the straight lines to calculate GIIP and JD.
Math & Physics
Combining the gas pseudo state flow equation and the Gas Material Balance equation to get Gas Flowing Material Balance equation:
where
Material balance pseudo-time:
Discussion
Gas Flowing Material Balance can be applied to:
- single well
- multiple wells producing from the same Reservoir.
The X axis on the Gas Flowing Material Balance Plot can be selected as:
Example 1. Multiple wells producing from the same Reservoir. X axis - Wells cumulative
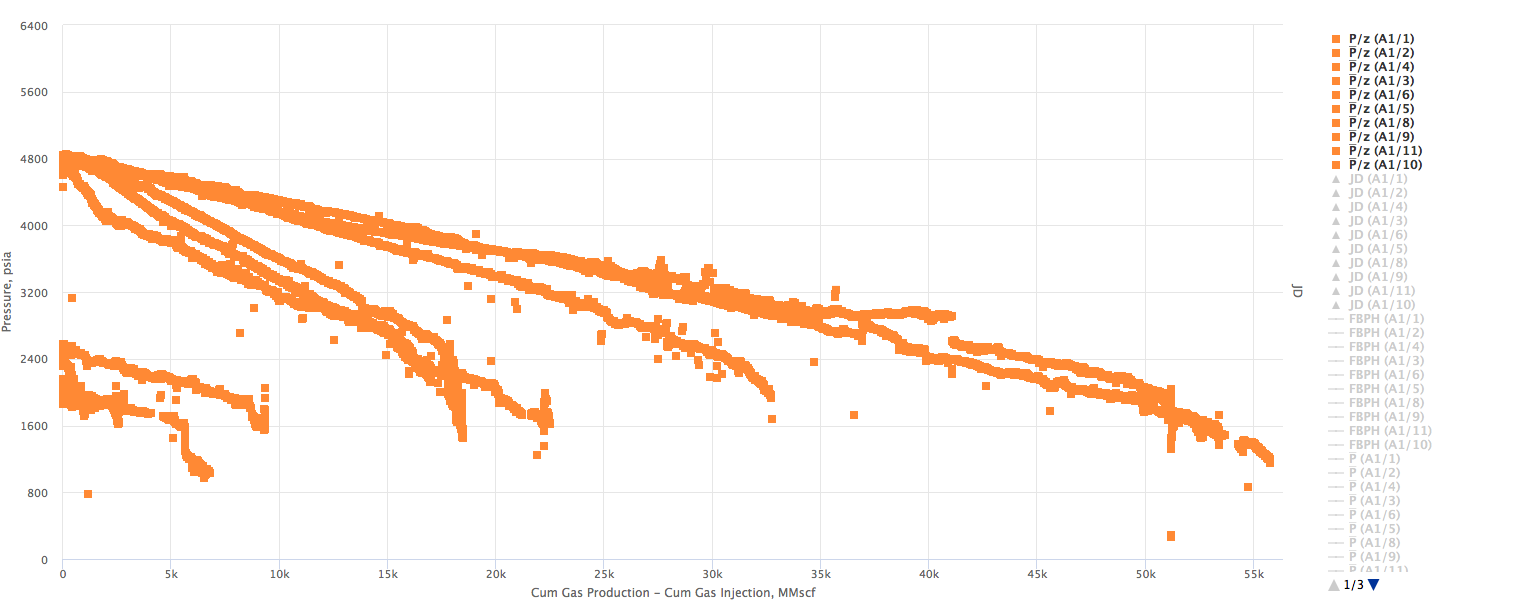 Example 2. Multiple wells producing from the same Reservoir. X axis - Reservoir cumulative
Example 2. Multiple wells producing from the same Reservoir. X axis - Reservoir cumulative
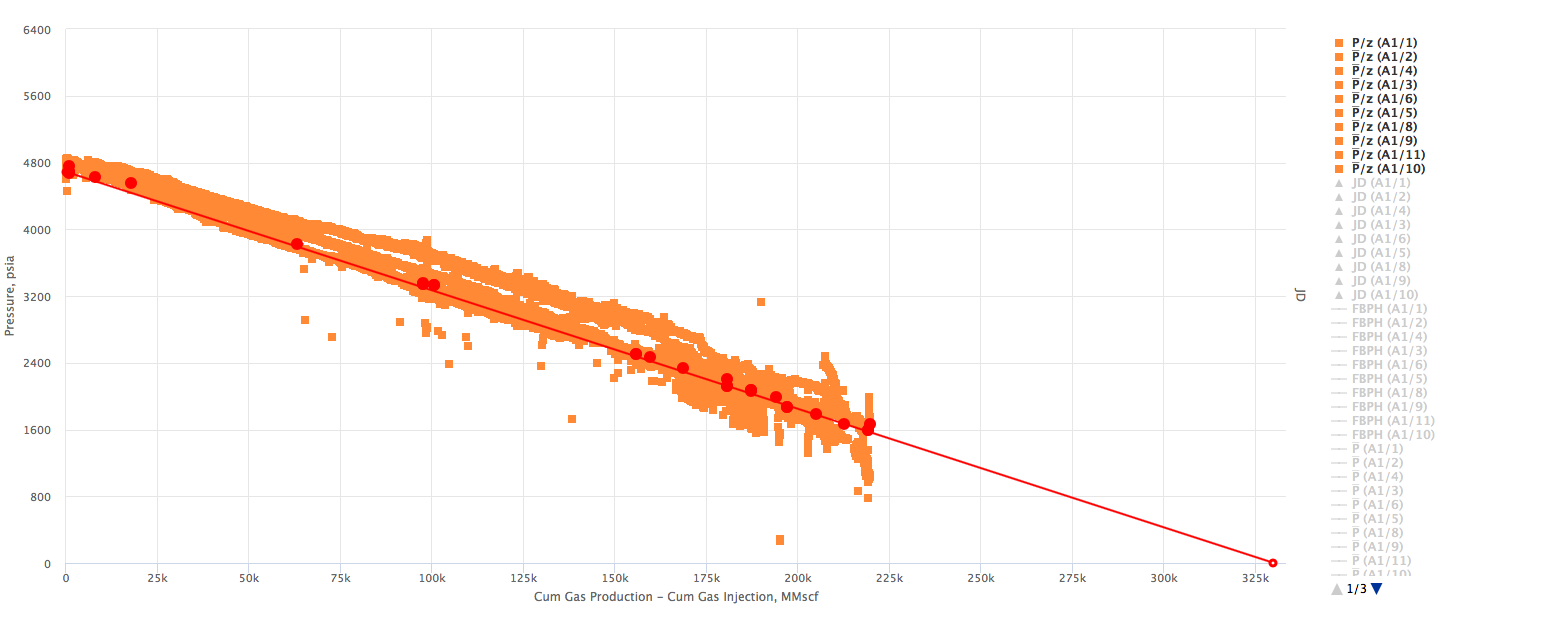 Example 3. Shifted Model Start (to account for gas injection)
Example 3. Shifted Model Start (to account for gas injection)
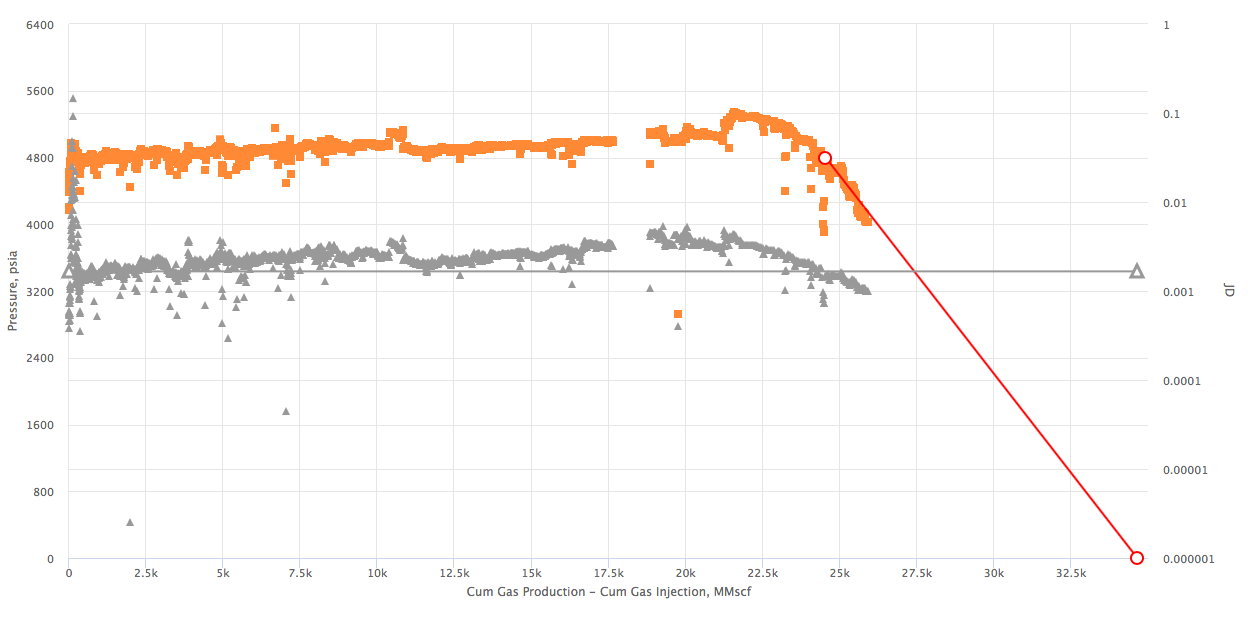
Workflow
- Upload the data required
- Open the Gas Flowing Material Balance tool here
- Calculate the red
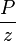 line:
line:
- Given the GIIP
- Calculate the
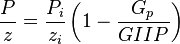
- Calculate the orange
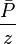 curve:
curve:
- Given the flowing wellhead pressures, calculate the flowing bottomhole pressures,
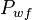
- Convert the flowing pressures to pseudopressures,
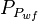
- Given the JD, calculate the
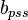
- Calculate the pseudopressure,
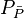
- Convert the pseudopressure to pressure,
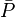
- Calculate the
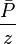
- Given the flowing wellhead pressures, calculate the flowing bottomhole pressures,
- Calculate the gray JD curve:
- Calculate the gas productivity index,
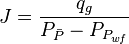
- Calculate the JD,
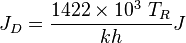
- Calculate the gas productivity index,
- Change the red
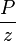 line to match the orange
line to match the orange 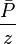 curve
curve
- Change the GIIP
- Change the intitial
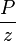
- Change the flat JD gray line to match the changing JD gray line
- Save the FMB model
- Move to the next well
Extra Plot to find bpss
- Calculate the initial pseudopressure,
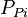
- Calculate the material balance pseudo-time,
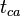
- Plot
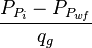 versus
versus 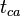
- The intercept with the Y axis gives
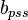 and
and 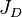
Data required
- Create Field here
- Create or Upload Reservoirs here
- Input the Reservoirs GIIP and STOIIP here
- Create or Upload PVT (SG, Pi, Ti) here
- Upload Wells
- Create or Upload Wells Perforations here
- Create or Upload kh and JD here
- Upload Daily Measures
In case you need to calculate the flowing bottomhole pressure from the wellhead pressure:
- Calculate the flowing bottomhole pressures using BHP Calculator
- Export flowing bottomhole pressures to Daily Measures here
In case you want to add the static reservoir pressures on the FMB Plot:
- Create or Upload the static reservoir pressures, here
- Calculate Monthly Measures from the Daily Measures using Monthly Data Calculator
Nomenclature
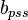 = reservoir constant, inverse to productivity index, psia2/cP/MMscfd
= reservoir constant, inverse to productivity index, psia2/cP/MMscfd = compressibility, psia-1
= compressibility, psia-1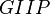 = gas initially in place, MMscf
= gas initially in place, MMscf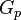 = cumulative gas produced, MMscf
= cumulative gas produced, MMscf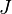 = gas productivity index, MMscfd/(psia2/cP)
= gas productivity index, MMscfd/(psia2/cP)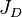 = dimensionless productivity index, dimensionless
= dimensionless productivity index, dimensionless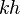 = permeability times thickness, md*ft
= permeability times thickness, md*ft = pressure, psia
= pressure, psia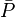 = average reservoir pressure, psia
= average reservoir pressure, psia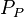 = pseudopressure, psia2/cP
= pseudopressure, psia2/cP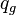 = gas rate, MMscfd
= gas rate, MMscfd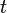 = time, day
= time, day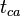 = material balance pseudotime for gas, day
= material balance pseudotime for gas, day = temperature, °R
= temperature, °R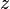 = gas compressibility factor, dimensionless
= gas compressibility factor, dimensionless
Greek symbols
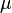 = viscosity, cp
= viscosity, cp
Subscripts
- g = gas
- i = initial
- R = °R
- wf = well flowing
References
- ↑ Mattar, L.; McNeil, R. (1998). "The "Flowing" Gas Material Balance" (PDF). Journal of Canadian Petroleum Technology. Petroleum Society of Canada.
- ↑ Mattar, L.; Anderson, D (2005). "Dynamic Material Balance (Oil or Gas-In-Place Without Shut-Ins)" (PDF). CIPC.