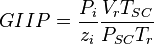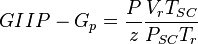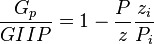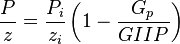Difference between revisions of "P/Z plot"

From wiki.pengtools.com
Jump to: navigation, search
(→‎Math & Physics)
 
(81 intermediate revisions by the same user not shown)
Line 1: Line 1:
 
__TOC__
 
__TOC__
 
== Brief ==
 
== Brief ==
−
The [[P/Z plot]] is a plot of P/Z versus cumulative gas production, G<sub>p</sub>.
+
The [[P/Z plot]] is a plot of P/z versus [[Reservoirs | Reservoir]] cumulative gas production, G<sub>p</sub>.
  
 
The interpretation technique is fitting the data points with the straight line to estimate GIIP.
 
The interpretation technique is fitting the data points with the straight line to estimate GIIP.
 +
 +
The [[P/Z plot]] is based on the [[Gas Material Balance]] equation.
 +
 +
[[File:PoverZ.png|thumb|right|600px|link=https://ep.pengtools.com/reservoir/plots| P/Z plot at ep.pengtools.com|right]]
  
 
== Math & Physics ==
 
== Math & Physics ==
  
−
The [[P/Z plot]] is based on the [[Gas Material Balance]] equation.
+
Applying [[Real Gas]] [[EOS]] at reservoir conditions:
 +
:<math> PV_r=z\frac{m}{M} RT_r</math>    (1)
 +
 
 +
Applying [[Real Gas]] [[EOS]] at standard conditions:
 +
:<math> P_{SC}V_g=1\frac{m}{M} RT_{SC}</math>    (2)
 +
 
 +
Dividing eq. 2 by eq. 1 and rearranging:
 +
:<math> V_g=\frac{P}{z} \frac{V_rT_{SC}}{P_{SC}T_{r}}</math>    (3)
 +
 
 +
Applying eq. 3 for initial conditions and for any point in time:
 +
:<math> GIIP=\frac{P_i}{z_i} \frac{V_rT_{SC}}{P_{SC}T_{r}}</math>
  
−
:<math> P_rV_r=z\frac{m}{M} RT_r</math> (1)
+
Applying eq. 3 for any point in time:
 +
:<math> GIIP-G_p=\frac{P}{z} \frac{V_rT_{SC}}{P_{SC}T_{r}}</math>
  
−
:<math> P_{SC}V_g=1\frac{m}{M} RT_{SC}</math> (2)
+
Therefore at any time:
 +
:<math> \frac{G_p}{GIIP}=1-\frac{P}{z} \frac{z_i}{P_i}</math>
  
−
(1) -> (2)
+
Or:
 +
:<math> \frac{P}{z}=\frac{P_i}{z_i} \left (1- \frac{G_p}{GIIP}\right )</math>
  
−
:<math> V_g=\frac{P}{z}\frac{V_rT_{SC}}{P_{SC}T_r}</math> (3)
+
Thus a plot of P/z vs cumulative produced gas is a straight line intersecting X axis at GIIP.
  
 +
== Discussion  ==
  
−
The bubble flow exist when:
+
[[P/Z plot]] is a part of the [[Reservoir Management]] workflow in the [[:Category:E&P Portal | E&P Portal]] used to estimate [[Reservoirs]] GIIP and recovery.
−
:<math> \frac{v_g}{v_g + v_L} < L_B </math><ref name= Economides />
 
  
−
:<math> L_B = 1.071 - 0.2218 \frac{(v_g+v_L)^2}{D}</math>, with the limit <math> L_B \geqslant 0.13 </math><ref name= Orkiszewski />
+
'''Example 1. Multiple Reservoirs on the same [[P/Z plot]]''' in the [[:Category:E&P Portal | E&P Portal]]
  
−
The gas holdup:
+
[[File:Poverz_multiple_reservoirs.png]]
−
:<math> H_g = \frac{1}{2}\ \left ( 1 + \frac{v_g+v_L}{v_s} - \sqrt{ \left ( 1 + \frac{v_g+v_L}{v_s} \right )^2 - 4 \frac{v_g}{v_s}}  \right ) </math><ref name= Orkiszewski />
 
  
−
== Discussion  ==
 
  
−
[[Griffith correlation]] adds a hook to the originally straight [[Hagedorn and Brown]] VLP curve.
+
[[Gas Flowing Material Balance]] is the more advanced tool to determine the [[Reservoirs]] GIIP and recovery as well as [[Well]]'s [[EUR]] and [[JD]].
  
−
== Nomenclature ==
+
== Workflow ==
 +
# Upload the data required
 +
# Go to the [[Reservoir Management]] -> [https://ep.pengtools.com/reservoir/plots Performance Plots]
 +
# Select the [[Reservoirs]] you want to see and the Data range and click "Search"
 +
# Scroll down the Performance Plots to see the [[P/Z plot]]
  
−
:<math> D </math> = pipe diameter, ft
+
=== Data Required===
−
:<math> H_g </math> = gas holdup factor, dimensionless
+
{{Data required for Reservoir Management}}
−
:<math> L_B </math> = bubble-slug boundary, dimensionless
 
−
:<math> v_g </math> = gas velocity, ft/sec
 
−
:<math> v_L </math> = liquid velocity, ft/sec
 
−
:<math> v_s </math> = 0.8, slip velocity (difference between average gas and liquid velocities), ft/sec
 
  
−
== References ==
+
== See also ==
−
<references>
+
[[Gas Flowing Material Balance]]<BR/>
 +
[[Gas Material Balance]]<BR/>
  
−
<ref name= Griffith>{{cite journal
+
== Nomenclature ==
−
|last1= Griffith |first1=P.
 
−
|last2= Wallis |first2=G. B.
 
−
|title=Two-Phase Slug Flow
 
−
|journal=Journal of Heat Transfer
 
−
|publisher = ASME
 
−
|date=August 1961
 
−
|volume=83
 
−
|pages=307-320
 
−
  |url=http://heattransfer.asmedigitalcollection.asme.org/article.aspx?articleid=1432339&resultClick=3
 
−
|url-access= subscription
 
−
}}</ref>
 
  
−
<ref name= Orkiszewski>{{cite journal
+
:<math> GIIP </math> = gas initially in place, scf
−
|last1= Orkiszewski |first1=J.
+
:<math> G_p </math> = cumulative gas produced, scf
−
|title=Predicting Two-Phase Pressure Drops in Vertical Pipe
+
:<math> P </math> = reservoir pressure (changing), psia
−
|journal=Journal of Petroleum Technology
+
:<math> P_{i} </math> = initial reservoir pressure (constant), psia
−
|publisher = SPE
+
:<math> P_{SC} </math> = pressure at standard conditions, psia
−
|number = SPE-1546-PA
+
:<math> T_i </math> = initial reservoir temperature (constant), °R
−
|date=June 1967
+
:<math> T_r </math> = reservoir temperature (constant), °R
−
|volume=19
+
:<math> T_{SC} </math> = temperature at standard conditions (constant), °R
−
|url=https://www.onepetro.org/journal-paper/SPE-1546-PA
+
:<math> V_g </math> = volume of gas in reservoir converted to standard conditions (changing), scf
−
|url-access= subscription
+
:<math> V_r </math> = reservoir volume (constant), ft<sup>3</sup>
−
}}</ref>
+
:<math> z </math> = gas compressibility factor (changing), dimensionless
 +
:<math> z_i </math> = initial gas compressibility factor (constant), dimensionless
  
−
<ref name=Economides>{{cite book
+
[[Category:Reservoir Management]]
−
|last1= Economides |first1=M.J.
+
[[Category:E&P Portal]]
−
|last2= Hill |first2=A.D.
 
−
|last3= Economides |first3=C.E.
 
−
|last4= Zhu |first4=D.
 
−
|title=Petroleum Production Systems
 
−
|edition=2
 
−
|date=2013
 
−
|publisher=Prentice Hall
 
−
|place=Westford, Massachusetts
 
−
|isbn=978-0-13-703158-0
 
−
}}</ref>
 
−
</references>
 
  
−
[[Category:pengtools]]
+
{{#seo:
−
[[Category:PQplot]]
+
|title=P/Z plot to estimate reservoirs GIIP
 +
|titlemode= replace
 +
|keywords=giip calculation, reservoir engineering, material balance, petroleum engineering
 +
|description=P/Z plot is and quick and easy to use tool to estimate reservoirs GIIP.
 +
}}

Latest revision as of 05:22, 8 November 2018

Brief

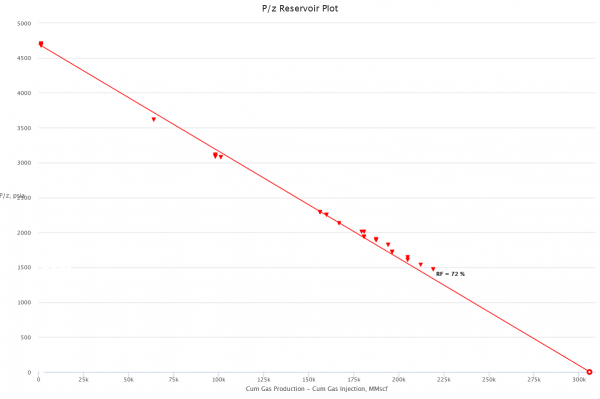
The P/Z plot is a plot of P/z versus Reservoir cumulative gas production, Gp.

The interpretation technique is fitting the data points with the straight line to estimate GIIP.

The P/Z plot is based on the Gas Material Balance equation.

P/Z plot at ep.pengtools.com

Math & Physics

Applying Real Gas EOS at reservoir conditions:

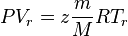PV_r=z\frac{m}{M} RT_r (1)

Applying Real Gas EOS at standard conditions:

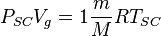P_{SC}V_g=1\frac{m}{M} RT_{SC} (2)

Dividing eq. 2 by eq. 1 and rearranging:

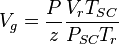V_g=\frac{P}{z} \frac{V_rT_{SC}}{P_{SC}T_{r}} (3)

Applying eq. 3 for initial conditions and for any point in time:

GIIP=\frac{P_i}{z_i} \frac{V_rT_{SC}}{P_{SC}T_{r}}

Applying eq. 3 for any point in time:

GIIP-G_p=\frac{P}{z} \frac{V_rT_{SC}}{P_{SC}T_{r}}

Therefore at any time:

\frac{G_p}{GIIP}=1-\frac{P}{z} \frac{z_i}{P_i}

Or:

\frac{P}{z}=\frac{P_i}{z_i} \left (1- \frac{G_p}{GIIP}\right )

Thus a plot of P/z vs cumulative produced gas is a straight line intersecting X axis at GIIP.

Discussion

P/Z plot is a part of the Reservoir Management workflow in the E&P Portal used to estimate Reservoirs GIIP and recovery.

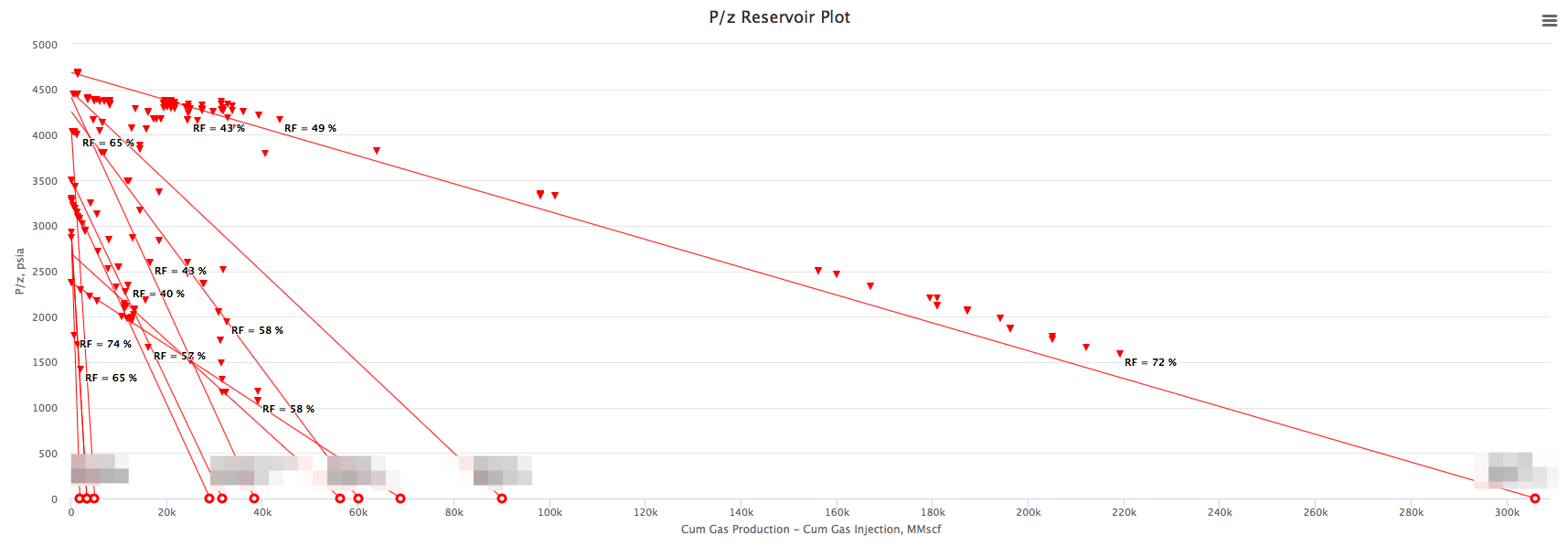
Example 1. Multiple Reservoirs on the same P/Z plot in the E&P Portal

Poverz multiple reservoirs.png


Gas Flowing Material Balance is the more advanced tool to determine the Reservoirs GIIP and recovery as well as Well's EUR and JD.

Workflow

  1. Upload the data required
  2. Go to the Reservoir Management -> Performance Plots
  3. Select the Reservoirs you want to see and the Data range and click "Search"
  4. Scroll down the Performance Plots to see the P/Z plot

Data Required

In case you need to calculate the Monthly Measures from the Daily Measures:

See also

Gas Flowing Material Balance
Gas Material Balance

Nomenclature

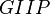GIIP = gas initially in place, scf
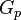G_p = cumulative gas produced, scf
P = reservoir pressure (changing), psia
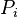P_{i} = initial reservoir pressure (constant), psia
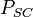P_{SC} = pressure at standard conditions, psia
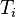T_i = initial reservoir temperature (constant), °R
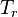T_r = reservoir temperature (constant), °R
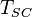T_{SC} = temperature at standard conditions (constant), °R
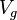V_g = volume of gas in reservoir converted to standard conditions (changing), scf
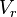V_r = reservoir volume (constant), ft3
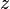z = gas compressibility factor (changing), dimensionless
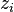z_i = initial gas compressibility factor (constant), dimensionless
Retrieved from "https://wiki.pengtools.com/index.php?title=P/Z_plot&oldid=5396"