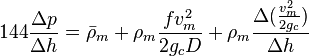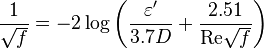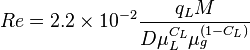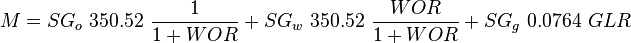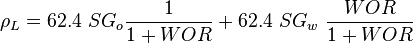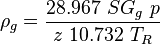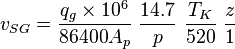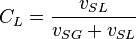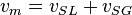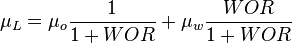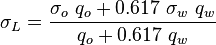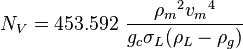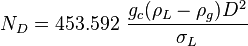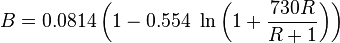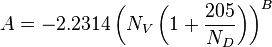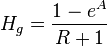Difference between revisions of "Gray correlation"

From wiki.pengtools.com
Jump to: navigation, search
(→‎Math & Physics)
 
(28 intermediate revisions by the same user not shown)
Line 2: Line 2:
 
== Brief ==
 
== Brief ==
  
−
[[Gray]] is an empirical two-phase flow correlation published in '''1974''' <ref name= Gray />.
+
[[Gray correlation|Gray]] is an empirical two-phase flow correlation published in '''1974''' <ref name= Gray />.
  
−
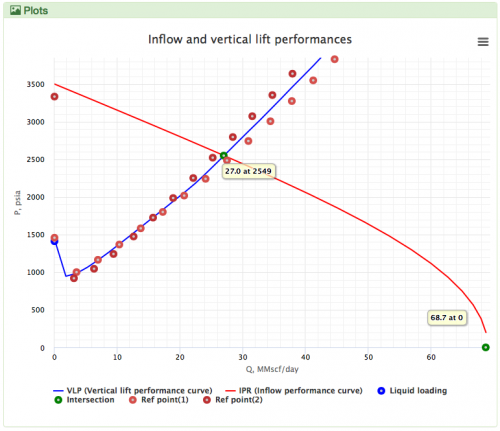
[[Gray]] is the default [[VLP]] correlation for the '''gas wells''' in the [[:Category:PqPlot|PQplot]].
+
[[Gray correlation|Gray]] is the default [[VLP]] correlation for the '''gas wells''' in the [[PQplot]].
 +
 
 +
[[File: GRAY.png|thumb|500px|link=https://www.pengtools.com/pqPlot?paramsToken=d14638acea57a4523b4553153a5dcb5a|Gray in PQplot Vs Prosper & Kappa |right]]
  
 
== Math & Physics ==
 
== Math & Physics ==
 
Following the law of conservation of energy the basic steady state flow equation is:
 
Following the law of conservation of energy the basic steady state flow equation is:
−
:<math> 144 \frac{\Delta p}{\Delta h} =  \bar \rho_m + \rho_m \frac{f v_m^2 }{2 g_c D} + \rho_m \frac{\Delta{(\frac{v_m^2}{2g_c}})}{\Delta h}</math><ref name="HB" />
+
:<math> 144 \frac{\Delta p}{\Delta h} =  \bar \rho_m + \rho_m \frac{f v_m^2 }{2 g_c D} + \rho_m \frac{\Delta{(\frac{v_m^2}{2g_c}})}{\Delta h}</math>
  
 
where
 
where
Line 29: Line 31:
 
== Discussion  ==
 
== Discussion  ==
  
−
Why [[Gray]] correlation?
+
Why [[Gray correlation|Gray]] correlation?
  
 
{{Quote| text = The Gray correlation was found to be the best of several initially tested ... | source = Nitesh Kumar l<ref name= Kumar />}}
 
{{Quote| text = The Gray correlation was found to be the best of several initially tested ... | source = Nitesh Kumar l<ref name= Kumar />}}
Line 37: Line 39:
 
:<math> M =SG_o\ 350.52\ \frac{1}{1+WOR}+SG_w\ 350.52\ \frac{WOR}{1+WOR}+SG_g\ 0.0764\ GLR</math><ref name="HB" />
 
:<math> M =SG_o\ 350.52\ \frac{1}{1+WOR}+SG_w\ 350.52\ \frac{WOR}{1+WOR}+SG_g\ 0.0764\ GLR</math><ref name="HB" />
  
−
:<math> \rho_L= \frac{62.4\ SG_o + \frac{Rs\ 0.0764\ SG_g}{5.614}}{B_o} \frac{1}{1+WOR} + 62.4\ SG_w\ \frac{WOR}{1 + WOR}</math><ref name= Lyons/>
+
:<math> \rho_L= 62.4\ SG_o \frac{1}{1+WOR} + 62.4\ SG_w\ \frac{WOR}{1 + WOR}</math>
  
 
:<math> \rho_g = \frac{28.967\ SG_g\ p}{z\ 10.732\ T_R} </math><ref name= Lyons/>
 
:<math> \rho_g = \frac{28.967\ SG_g\ p}{z\ 10.732\ T_R} </math><ref name= Lyons/>
Line 69: Line 71:
 
== Modifications  ==
 
== Modifications  ==
  
−
1. Use watercut instead of WOR to account for the OGR=0 case.
+
1. Use [[Fanning correlation]] for the dry gas ([[WGR]]=0 and [[OGR]]=0 case).
 +
 
 +
2. Use [[WCUT| watercut]] instead of [[WOR]] to account for the [[OGR]]=0 case.
 +
 
 +
3. If the relative roughness: <math> \frac{\varepsilon'}{D} > 0.05 </math> use 0.05 in the Moody Diagram <ref name = Moody1944/>.
 +
 
 +
4. If H<sub>L</sub> can't be calculated then H<sub>L</sub> = C<sub>L</sub>.
  
 
== Nomenclature  ==
 
== Nomenclature  ==
Line 87: Line 95:
 
:<math> N_V </math> = velocity number, dimensionless
 
:<math> N_V </math> = velocity number, dimensionless
 
:<math> p </math> = pressure, psia
 
:<math> p </math> = pressure, psia
−
:<math> q_c </math> = conversion constant equal to 32.174, lb<sub>m</sub>ft / lb<sub>f</sub>sec<sup>2</sup>
+
:<math> q_c </math> = conversion constant equal to 32.174049, lb<sub>m</sub>ft / lb<sub>f</sub>sec<sup>2</sup>
 
:<math> q </math> = production rate, bbl/d
 
:<math> q </math> = production rate, bbl/d
 
:<math> R </math> = superficial liquid to gas ratio, dimensionless
 
:<math> R </math> = superficial liquid to gas ratio, dimensionless
 
:<math> Re </math> = Reynolds number, dimensionless
 
:<math> Re </math> = Reynolds number, dimensionless
−
:<math> R_s </math> = solution gas-oil ratio, scf/stb
 
 
:<math> SG </math> = specific gravity, dimensionless
 
:<math> SG </math> = specific gravity, dimensionless
 
:<math> T </math> = temperature, °R or °K, follow the subscript
 
:<math> T </math> = temperature, °R or °K, follow the subscript
Line 188: Line 195:
  
 
[[Category:pengtools]]
 
[[Category:pengtools]]
−
[[Category:pqPlot]]
+
[[Category:PQplot]]
 +
 
 +
{{#seo:
 +
|title=Gray correlation
 +
|titlemode= replace
 +
|keywords=Gray correlation
 +
|description=Gray correlation is an empirical two-phase flow correlation published in 1974.
 +
}}

Latest revision as of 09:10, 6 December 2018

Brief

Gray is an empirical two-phase flow correlation published in 1974 [1].

Gray is the default VLP correlation for the gas wells in the PQplot.

Gray in PQplot Vs Prosper & Kappa

Math & Physics

Following the law of conservation of energy the basic steady state flow equation is:

144 \frac{\Delta p}{\Delta h} = \bar \rho_m + \rho_m \frac{f v_m^2 }{2 g_c D} + \rho_m \frac{\Delta{(\frac{v_m^2}{2g_c}})}{\Delta h}

where

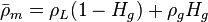\bar \rho_m = \rho_L (1-H_g) + \rho_g H_g, slip mixture density [1].
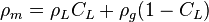\rho_m = \rho_L C_L + \rho_g (1-C_L) , no-slip mixture density [1].

Colebrook–White [2] equation for the Darcy's friction factor:

\frac{1}{\sqrt{f}}= -2 \log \left( \frac { \varepsilon'} {3.7 D} + \frac {2.51} {\mathrm{Re} \sqrt{f}} \right)[3]

The pseudo wall roughness:

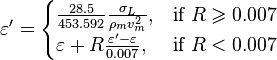\varepsilon' = \begin{cases} \frac{28.5}{453.592} \frac{\sigma_L}{\rho_m v_m^2}, &\mbox{if } R \geqslant 0.007 \\ \varepsilon + R \frac{\varepsilon'-\varepsilon}{0.007}, & \mbox{if } R < 0.007 \end{cases} , with the limit 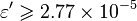\varepsilon' \geqslant 2.77 \times 10^{-5}[1]

Reynolds two phase number:

Re = 2.2 \times 10^{-2} \frac {q_L M}{D \mu_L^{C_L} \mu_g^{(1-C_L)}}[4]

Discussion

Why Gray correlation?

The Gray correlation was found to be the best of several initially tested ...
— Nitesh Kumar l[5]

Workflow Hg & CL

M =SG_o\ 350.52\ \frac{1}{1+WOR}+SG_w\ 350.52\ \frac{WOR}{1+WOR}+SG_g\ 0.0764\ GLR[4]
\rho_L= 62.4\ SG_o \frac{1}{1+WOR} + 62.4\ SG_w\ \frac{WOR}{1 + WOR}
\rho_g = \frac{28.967\ SG_g\ p}{z\ 10.732\ T_R} [6]
v_{SL} = \frac{5.615 q_L}{86400 A_p} \left ( B_o \frac{1}{1+WOR} + B_w \frac{WOR}{1+WOR} \right )[6]
v_{SG} = \frac{q_g \times 10^6}{86400 A_p}\ \frac{14.7}{p}\ \frac{T_K}{520}\ \frac{z}{1}
C_L = \frac{v_{SL}}{v_{SG}+v_{SL}}
v_m = v_{SL} + v_{SG}
\rho_m = \rho_L C_L + \rho_g (1-C_L)
\mu_L = \mu_o \frac{1}{1 + WOR} + \mu_w \frac{WOR}{1 + WOR}[6]
\sigma_L = \frac{\sigma_o\ q_o + 0.617\ \sigma_w\ q_w}{q_o + 0.617\ q_w} [1]
N_V = 453.592\ \frac{{\rho_m}^2 {v_m}^4}{g_c \sigma_L (\rho_L - \rho_g)} [1]
N_D = 453.592\ \frac{g_c (\rho_L - \rho_g) D^2}{\sigma_L } [1]
R = \frac{v_{SL}}{v_{SG}} [1]
B = 0.0814 \left ( 1 - 0.554\ \ln \left (1 + \frac{730 R}{R+1} \right ) \right ) [1]
A = -2.2314 \left ( N_V \left (1 + \frac{205}{N_D} \right ) \right )^B [1]
H_g = \frac{1-e^A}{R+1}[1]

Modifications

1. Use Fanning correlation for the dry gas (WGR=0 and OGR=0 case).

2. Use watercut instead of WOR to account for the OGR=0 case.

3. If the relative roughness: 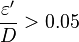\frac{\varepsilon'}{D} > 0.05 use 0.05 in the Moody Diagram [3].

4. If HL can't be calculated then HL = CL.

Nomenclature

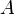A = correlation group, dimensionless
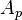A_p = flow area, ft2
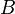B = correlation group, dimensionless
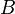B = formation factor, bbl/stb
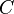C = no-slip holdup factor, dimensionless
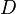D = pipe diameter, ft
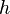h = depth, ft
H = holdup factor, dimensionless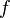
f = friction factor, dimensionless
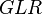GLR = gas-liquid ratio, scf/bbl
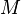M = total mass of oil, water and gas associated with 1 bbl of liquid flowing into and out of the flow string, lbm/bbl
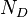N_D = pipe diameter number, dimensionless
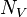N_V = velocity number, dimensionless
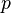p = pressure, psia
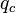q_c = conversion constant equal to 32.174049, lbmft / lbfsec2
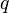q = production rate, bbl/d
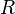R = superficial liquid to gas ratio, dimensionless
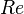Re = Reynolds number, dimensionless
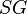SG = specific gravity, dimensionless
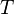T = temperature, °R or °K, follow the subscript
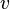v = velocity, ft/sec
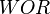WOR = water-oil ratio, bbl/bbl
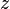z = gas compressibility factor, dimensionless

Greek symbols

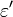\varepsilon = absolute roughness, ft
\varepsilon' = pseudo wall roughness, ft
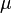\mu = viscosity, cp
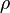\rho = density, lbm/ft3
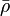\bar \rho = slip density, lbm/ft2
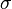\sigma = surface tension of liquid-air interface, dynes/cm

Subscripts

g = gas
K = °K
L = liquid
m = gas/liquid mixture
o = oil
R = °R
SL = superficial liquid
SG = superficial gas
w = water

References

  1. ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 Gray, H. E. (1974). "Vertical Flow Correlation in Gas Wells". User manual for API 14B, Subsurface controlled safety valve sizing computer program. API. 
  2. ↑ Colebrook, C. F. (1938–1939). "Turbulent Flow in Pipes, With Particular Reference to the Transition Region Between the Smooth and Rough Pipe Laws"Paid subscription required. Journal of the Institution of Civil Engineers. London, England. 11: 133–156. 
  3. ↑ 3.0 3.1 Moody, L. F. (1944). "Friction factors for pipe flow"Paid subscription required. Transactions of the ASME. 66 (8): 671–684. 
  4. ↑ 4.0 4.1 Hagedorn, A. R.; Brown, K. E. (1965). "Experimental study of pressure gradients occurring during continuous two-phase flow in small-diameter vertical conduits". Journal of Petroleum Technology. 17(04): 475–484. 
  5. ↑ Kumar, N.; Lea, J. F. (January 1, 2005). "Improvements for Flow Correlations for Gas Wells Experiencing Liquid Loading"Free registration required (SPE-92049-MS). 
  6. ↑ 6.0 6.1 6.2 Lyons, W.C. (1996). Standard handbook of petroleum and natural gas engineering. 2. Houston, TX: Gulf Professional Publishing. ISBN 0-88415-643-5. 
Retrieved from "https://wiki.pengtools.com/index.php?title=Gray_correlation&oldid=5457"