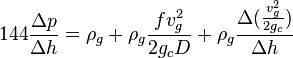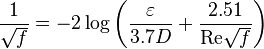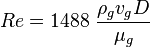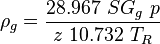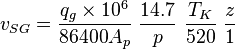Fanning correlation

Brief

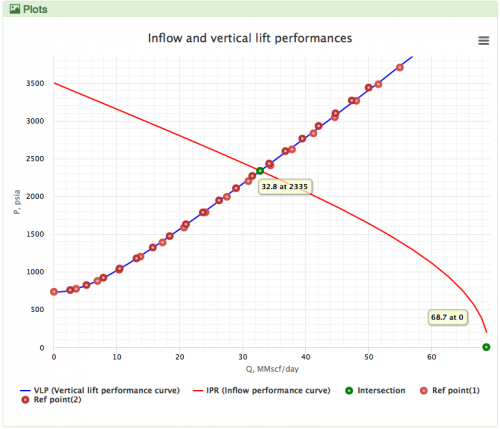
The Fanning correlation is the name used to refer to the calculation of the hydrostatic pressure difference and the friction pressure loss for the dry gas flow.

Fanning correlation is the default VLP correlation for the dry gas wells in the PQplot.

Fanning in PQplot Vs Prosper & Kappa

Math & Physics

Following the law of conservation of energy the basic steady state flow equation is:

$144 \frac{\Delta p}{\Delta h} = \rho_g + \rho_g \frac{f v_g^2 }{2 g_c D} + \rho_g \frac{\Delta{(\frac{v_g^2}{2g_c}})}{\Delta h}$

Colebrook–White equation for the Darcy's friction factor:

$\frac{1}{\sqrt{f}}= -2 \log \left( \frac { \varepsilon} {3.7 D} + \frac {2.51} {\mathrm{Re} \sqrt{f}} \right)$

Reynolds number:

$Re = 1488\ \frac {\rho_g v_g D}{\mu_g}$

$\rho_g = \frac{28.967\ SG_g\ p}{z\ 10.732\ T_R}$

$v_{SG} = \frac{q_g \times 10^6}{86400 A_p}\ \frac{14.7}{p}\ \frac{T_K}{520}\ \frac{z}{1}$

Discussion

Why Fanning correlation ?

Fanning correlation actually is not a correlation, it's the fully explicit workflow to define the pressure drop.

— www.pengtools.com

Nomenclature

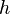$h$ = depth, ft

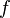$f$ = friction factor, dimensionless

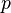$p$ = pressure, psia

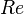$Re$ = Reynolds number, dimensionless

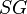$SG$ = specific gravity, dimensionless

$T$ = temperature, °R or °K, follow the subscript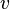

$v$ = velocity, ft/sec

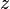$z$ = gas compressibility factor, dimensionless

Greek symbols

$\varepsilon$ = absolute roughness, ft

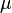$\mu$ = viscosity, cp

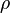$\rho$ = density, lb_m/ft³

Subscripts

g = gas
K = °K
L = liquid
R = °R
SG = superficial gas

References

[[Category:sPipe]