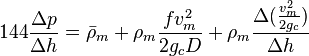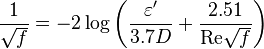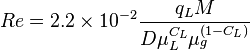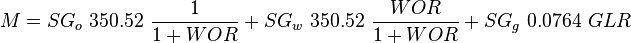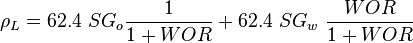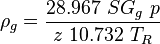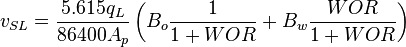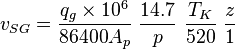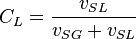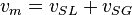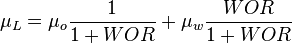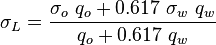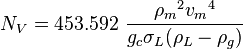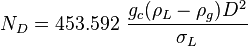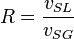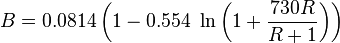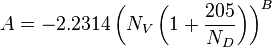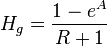Difference between revisions of "Gray correlation"
(→Workflow) |
|||
| (131 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
== Brief == | == Brief == | ||
| − | + | [[Gray correlation|Gray]] is an empirical two-phase flow correlation published in '''1974''' <ref name= Gray />. | |
| + | |||
| + | [[Gray correlation|Gray]] is the default [[VLP]] correlation for the '''gas wells''' in the [[PQplot]]. | ||
| + | |||
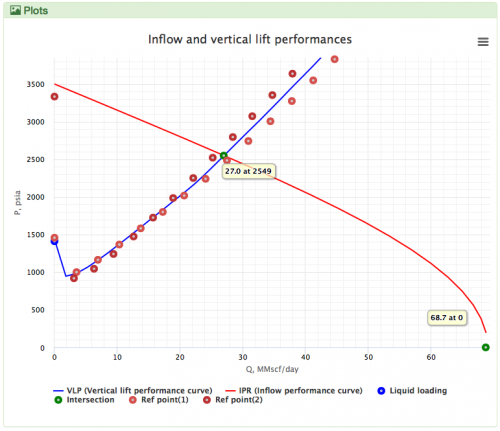
| + | [[File: GRAY.png|thumb|500px|link=https://www.pengtools.com/pqPlot?paramsToken=d14638acea57a4523b4553153a5dcb5a|Gray in PQplot Vs Prosper & Kappa |right]] | ||
== Math & Physics == | == Math & Physics == | ||
Following the law of conservation of energy the basic steady state flow equation is: | Following the law of conservation of energy the basic steady state flow equation is: | ||
| − | :<math> 144 \frac{\Delta p}{\Delta h} = | + | :<math> 144 \frac{\Delta p}{\Delta h} = \bar \rho_m + \rho_m \frac{f v_m^2 }{2 g_c D} + \rho_m \frac{\Delta{(\frac{v_m^2}{2g_c}})}{\Delta h}</math> |
where | where | ||
| − | :<math> \rho_m </math> = | + | :<math> \bar \rho_m = \rho_L (1-H_g) + \rho_g H_g</math>, slip mixture density <ref name= Gray />. |
| + | |||
| + | :<math> \rho_m = \rho_L C_L + \rho_g (1-C_L) </math>, no-slip mixture density <ref name= Gray />. | ||
Colebrook–White <ref name=Colebrook/> equation for the [http://en.wikipedia.org/wiki/Darcy_friction_factor_formulae Darcy's friction factor]: | Colebrook–White <ref name=Colebrook/> equation for the [http://en.wikipedia.org/wiki/Darcy_friction_factor_formulae Darcy's friction factor]: | ||
| − | :<math> \frac{1}{\sqrt{f}}= -2 \log \left( \frac { \varepsilon} {3.7 D} + \frac {2.51} {\mathrm{Re} \sqrt{f}} \right)</math><ref name = Moody1944/> | + | :<math> \frac{1}{\sqrt{f}}= -2 \log \left( \frac { \varepsilon'} {3.7 D} + \frac {2.51} {\mathrm{Re} \sqrt{f}} \right)</math><ref name = Moody1944/> |
| + | |||
| + | The pseudo wall roughness: | ||
| + | :<math> \varepsilon' = \begin{cases} | ||
| + | \frac{28.5}{453.592} \frac{\sigma_L}{\rho_m v_m^2}, &\mbox{if } R \geqslant 0.007 \\ | ||
| + | \varepsilon + R \frac{\varepsilon'-\varepsilon}{0.007}, & \mbox{if } R < 0.007 | ||
| + | \end{cases} </math>, with the limit <math> \varepsilon' \geqslant 2.77 \times 10^{-5}</math><ref name= Gray/> | ||
Reynolds two phase number: | Reynolds two phase number: | ||
| − | :<math> Re = 2.2 \times 10^{-2} \frac {q_L M}{D \mu_L^{ | + | :<math> Re = 2.2 \times 10^{-2} \frac {q_L M}{D \mu_L^{C_L} \mu_g^{(1-C_L)}}</math><ref name= HB/> |
== Discussion == | == Discussion == | ||
| − | == Workflow == | + | Why [[Gray correlation|Gray]] correlation? |
| + | |||
| + | {{Quote| text = The Gray correlation was found to be the best of several initially tested ... | source = Nitesh Kumar l<ref name= Kumar />}} | ||
| + | |||
| + | == Workflow H<sub>g</sub> & C<sub>L</sub>== | ||
| − | + | :<math> M =SG_o\ 350.52\ \frac{1}{1+WOR}+SG_w\ 350.52\ \frac{WOR}{1+WOR}+SG_g\ 0.0764\ GLR</math><ref name="HB" /> | |
| − | :<math> N_V = 453.592\ \frac{\ | + | :<math> \rho_L= 62.4\ SG_o \frac{1}{1+WOR} + 62.4\ SG_w\ \frac{WOR}{1 + WOR}</math> |
| + | |||
| + | :<math> \rho_g = \frac{28.967\ SG_g\ p}{z\ 10.732\ T_R} </math><ref name= Lyons/> | ||
| + | |||
| + | :<math> v_{SL} = \frac{5.615 q_L}{86400 A_p} \left ( B_o \frac{1}{1+WOR} + B_w \frac{WOR}{1+WOR} \right )</math><ref name= Lyons/> | ||
| + | |||
| + | :<math> v_{SG} = \frac{q_g \times 10^6}{86400 A_p}\ \frac{14.7}{p}\ \frac{T_K}{520}\ \frac{z}{1}</math> | ||
| + | |||
| + | :<math> C_L = \frac{v_{SL}}{v_{SG}+v_{SL}}</math> | ||
| + | |||
| + | :<math> v_m = v_{SL} + v_{SG} </math> | ||
| + | |||
| + | :<math> \rho_m = \rho_L C_L + \rho_g (1-C_L) </math> | ||
| + | |||
| + | :<math> \mu_L = \mu_o \frac{1}{1 + WOR} + \mu_w \frac{WOR}{1 + WOR}</math><ref name= Lyons/> | ||
| + | |||
| + | :<math> \sigma_L = \frac{\sigma_o\ q_o + 0.617\ \sigma_w\ q_w}{q_o + 0.617\ q_w}</math> <ref name= Gray/> | ||
| + | |||
| + | :<math> N_V = 453.592\ \frac{{\rho_m}^2 {v_m}^4}{g_c \sigma_L (\rho_L - \rho_g)} </math><ref name= Gray/> | ||
| + | |||
| + | :<math> N_D = 453.592\ \frac{g_c (\rho_L - \rho_g) D^2}{\sigma_L } </math><ref name= Gray/> | ||
| + | |||
| + | :<math> R = \frac{v_{SL}}{v_{SG}} </math><ref name= Gray/> | ||
| + | |||
| + | :<math> B = 0.0814 \left ( 1 - 0.554\ \ln \left (1 + \frac{730 R}{R+1} \right ) \right ) </math><ref name= Gray/> | ||
| + | |||
| + | :<math> A = -2.2314 \left ( N_V \left (1 + \frac{205}{N_D} \right ) \right )^B </math><ref name= Gray/> | ||
| + | |||
| + | :<math> H_g = \frac{1-e^A}{R+1}</math><ref name= Gray/> | ||
| + | |||
| + | == Modifications == | ||
| + | |||
| + | 1. Use [[Fanning correlation]] for the dry gas ([[WGR]]=0 and [[OGR]]=0 case). | ||
| + | |||
| + | 2. Use [[WCUT| watercut]] instead of [[WOR]] to account for the [[OGR]]=0 case. | ||
| + | |||
| + | 3. If the relative roughness: <math> \frac{\varepsilon'}{D} > 0.05 </math> use 0.05 in the Moody Diagram <ref name = Moody1944/>. | ||
| + | |||
| + | 4. If H<sub>L</sub> can't be calculated then H<sub>L</sub> = C<sub>L</sub>. | ||
== Nomenclature == | == Nomenclature == | ||
| + | |||
| + | :<math> A </math> = correlation group, dimensionless | ||
| + | :<math> A_p </math> = flow area, ft2 | ||
| + | :<math> B </math> = correlation group, dimensionless | ||
| + | :<math> B </math> = formation factor, bbl/stb | ||
| + | :<math> C </math> = no-slip holdup factor, dimensionless | ||
| + | :<math> D </math> = pipe diameter, ft | ||
| + | :<math> h </math> = depth, ft | ||
| + | :<math> H </math> = holdup factor, dimensionless | ||
| + | :<math> f </math> = friction factor, dimensionless | ||
| + | :<math> GLR </math> = gas-liquid ratio, scf/bbl | ||
| + | :<math> M </math> = total mass of oil, water and gas associated with 1 bbl of liquid flowing into and out of the flow string, lb<sub>m</sub>/bbl | ||
| + | :<math> N_D </math> = pipe diameter number, dimensionless | ||
| + | :<math> N_V </math> = velocity number, dimensionless | ||
| + | :<math> p </math> = pressure, psia | ||
| + | :<math> q_c </math> = conversion constant equal to 32.174049, lb<sub>m</sub>ft / lb<sub>f</sub>sec<sup>2</sup> | ||
| + | :<math> q </math> = production rate, bbl/d | ||
| + | :<math> R </math> = superficial liquid to gas ratio, dimensionless | ||
| + | :<math> Re </math> = Reynolds number, dimensionless | ||
| + | :<math> SG </math> = specific gravity, dimensionless | ||
| + | :<math> T </math> = temperature, °R or °K, follow the subscript | ||
| + | :<math> v </math> = velocity, ft/sec | ||
| + | :<math> WOR </math> = water-oil ratio, bbl/bbl | ||
| + | :<math> z </math> = gas compressibility factor, dimensionless | ||
| + | |||
| + | ===Greek symbols=== | ||
| + | |||
| + | :<math> \varepsilon </math> = absolute roughness, ft | ||
| + | :<math> \varepsilon' </math> = pseudo wall roughness, ft | ||
| + | :<math> \mu </math> = viscosity, cp | ||
| + | :<math> \rho </math> = density, lb<sub>m</sub>/ft<sup>3</sup> | ||
| + | :<math> \bar \rho </math> = slip density, lb<sub>m</sub>/ft<sup>2</sup> | ||
| + | :<math> \sigma </math> = surface tension of liquid-air interface, dynes/cm | ||
| + | |||
| + | ===Subscripts=== | ||
| + | |||
| + | g = gas<BR/> | ||
| + | K = °K<BR/> | ||
| + | L = liquid<BR/> | ||
| + | m = gas/liquid mixture<BR/> | ||
| + | o = oil<BR/> | ||
| + | R = °R<BR/> | ||
| + | SL = superficial liquid<BR/> | ||
| + | SG = superficial gas<BR/> | ||
| + | w = water<BR/> | ||
== References == | == References == | ||
| Line 62: | Line 161: | ||
|url-access=subscription | |url-access=subscription | ||
}} </ref> | }} </ref> | ||
| + | |||
| + | <ref name=HB>{{cite journal | ||
| + | |last1=Hagedorn|first1=A. R. | ||
| + | |last2= Brown |first2=K. E. | ||
| + | |title=Experimental study of pressure gradients occurring during continuous two-phase flow in small-diameter vertical conduits | ||
| + | |journal=Journal of Petroleum Technology | ||
| + | |date=1965 | ||
| + | |volume=17(04) | ||
| + | |pages=475-484 | ||
| + | }}</ref> | ||
| + | |||
| + | <ref name= Lyons>{{cite book | ||
| + | |last1= Lyons |first1=W.C. | ||
| + | |title=Standard handbook of petroleum and natural gas engineering | ||
| + | |date= 1996 | ||
| + | |volume=2 | ||
| + | |publisher=Gulf Professional Publishing | ||
| + | |place=Houston, TX | ||
| + | |isbn=0-88415-643-5 | ||
| + | }}</ref> | ||
| + | |||
| + | <ref name=Kumar>{{cite journal | ||
| + | |first1=N. |last1=Kumar | ||
| + | |first2=J. F. |last2=Lea | ||
| + | |title=Improvements for Flow Correlations for Gas Wells Experiencing Liquid Loading | ||
| + | |number=SPE-92049-MS | ||
| + | |date=January 1, 2005 | ||
| + | |url=https://www.onepetro.org/conference-paper/SPE-92049-MS | ||
| + | |url-access=registration | ||
| + | }}</ref> | ||
</references> | </references> | ||
[[Category:pengtools]] | [[Category:pengtools]] | ||
| − | [[Category: | + | [[Category:PQplot]] |
| + | |||
| + | {{#seo: | ||
| + | |title=Gray correlation | ||
| + | |titlemode= replace | ||
| + | |keywords=Gray correlation | ||
| + | |description=Gray correlation is an empirical two-phase flow correlation published in 1974. | ||
| + | }} | ||
Latest revision as of 09:10, 6 December 2018
Contents
Brief
Gray is an empirical two-phase flow correlation published in 1974 [1].
Gray is the default VLP correlation for the gas wells in the PQplot.
Math & Physics
Following the law of conservation of energy the basic steady state flow equation is:
where
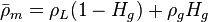 , slip mixture density [1].
, slip mixture density [1].
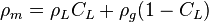 , no-slip mixture density [1].
, no-slip mixture density [1].
Colebrook–White [2] equation for the Darcy's friction factor:
The pseudo wall roughness:
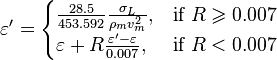 , with the limit
, with the limit 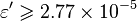 [1]
[1]
Reynolds two phase number:
Discussion
Why Gray correlation?
The Gray correlation was found to be the best of several initially tested ...— Nitesh Kumar l[5]
Workflow Hg & CL
Modifications
1. Use Fanning correlation for the dry gas (WGR=0 and OGR=0 case).
2. Use watercut instead of WOR to account for the OGR=0 case.
3. If the relative roughness: 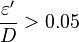 use 0.05 in the Moody Diagram [3].
use 0.05 in the Moody Diagram [3].
4. If HL can't be calculated then HL = CL.
Nomenclature
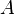 = correlation group, dimensionless
= correlation group, dimensionless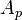 = flow area, ft2
= flow area, ft2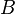 = correlation group, dimensionless
= correlation group, dimensionless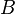 = formation factor, bbl/stb
= formation factor, bbl/stb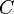 = no-slip holdup factor, dimensionless
= no-slip holdup factor, dimensionless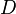 = pipe diameter, ft
= pipe diameter, ft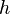 = depth, ft
= depth, ft = holdup factor, dimensionless
= holdup factor, dimensionless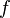 = friction factor, dimensionless
= friction factor, dimensionless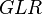 = gas-liquid ratio, scf/bbl
= gas-liquid ratio, scf/bbl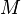 = total mass of oil, water and gas associated with 1 bbl of liquid flowing into and out of the flow string, lbm/bbl
= total mass of oil, water and gas associated with 1 bbl of liquid flowing into and out of the flow string, lbm/bbl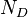 = pipe diameter number, dimensionless
= pipe diameter number, dimensionless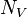 = velocity number, dimensionless
= velocity number, dimensionless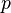 = pressure, psia
= pressure, psia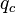 = conversion constant equal to 32.174049, lbmft / lbfsec2
= conversion constant equal to 32.174049, lbmft / lbfsec2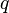 = production rate, bbl/d
= production rate, bbl/d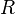 = superficial liquid to gas ratio, dimensionless
= superficial liquid to gas ratio, dimensionless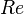 = Reynolds number, dimensionless
= Reynolds number, dimensionless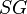 = specific gravity, dimensionless
= specific gravity, dimensionless = temperature, °R or °K, follow the subscript
= temperature, °R or °K, follow the subscript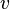 = velocity, ft/sec
= velocity, ft/sec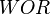 = water-oil ratio, bbl/bbl
= water-oil ratio, bbl/bbl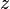 = gas compressibility factor, dimensionless
= gas compressibility factor, dimensionless
Greek symbols
 = absolute roughness, ft
= absolute roughness, ft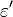 = pseudo wall roughness, ft
= pseudo wall roughness, ft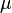 = viscosity, cp
= viscosity, cp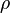 = density, lbm/ft3
= density, lbm/ft3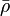 = slip density, lbm/ft2
= slip density, lbm/ft2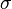 = surface tension of liquid-air interface, dynes/cm
= surface tension of liquid-air interface, dynes/cm
Subscripts
g = gas
K = °K
L = liquid
m = gas/liquid mixture
o = oil
R = °R
SL = superficial liquid
SG = superficial gas
w = water
References
- ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 Gray, H. E. (1974). "Vertical Flow Correlation in Gas Wells". User manual for API 14B, Subsurface controlled safety valve sizing computer program. API.
- ↑ Colebrook, C. F. (1938–1939). "Turbulent Flow in Pipes, With Particular Reference to the Transition Region Between the Smooth and Rough Pipe Laws"
 . Journal of the Institution of Civil Engineers. London, England. 11: 133–156.
. Journal of the Institution of Civil Engineers. London, England. 11: 133–156.
- ↑ 3.0 3.1 Moody, L. F. (1944). "Friction factors for pipe flow"
 . Transactions of the ASME. 66 (8): 671–684.
. Transactions of the ASME. 66 (8): 671–684.
- ↑ 4.0 4.1 Hagedorn, A. R.; Brown, K. E. (1965). "Experimental study of pressure gradients occurring during continuous two-phase flow in small-diameter vertical conduits". Journal of Petroleum Technology. 17(04): 475–484.
- ↑ Kumar, N.; Lea, J. F. (January 1, 2005). "Improvements for Flow Correlations for Gas Wells Experiencing Liquid Loading"
 (SPE-92049-MS).
(SPE-92049-MS).
- ↑ 6.0 6.1 6.2 Lyons, W.C. (1996). Standard handbook of petroleum and natural gas engineering. 2. Houston, TX: Gulf Professional Publishing. ISBN 0-88415-643-5.