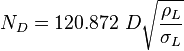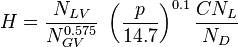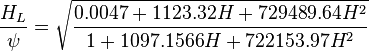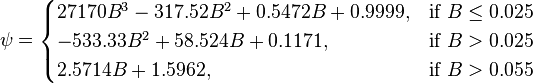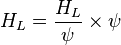Difference between revisions of "Hagedorn and Brown correlation"
(→Demo) |
|||
| (8 intermediate revisions by the same user not shown) | |||
| Line 31: | Line 31: | ||
== Demo == | == Demo == | ||
| − | [[File:Hagedorn and Brown demo.png| | + | [[Hagedorn and Brown]] correlation overview video: |
| + | |||
| + | [[File:Hagedorn and Brown demo.png|400px|https://www.youtube.com/watch?v=DpSv3kWPsIk | Watch on youtube]] | ||
| + | |||
| + | [[Media:Hagedorn and Brown ppt.pdf|Download presentation (pdf)]] | ||
| + | |||
| + | In this video it's shown: | ||
| + | *What the Hagedorn and Brown correlation is | ||
| + | *History and practical application | ||
| + | *Math & Physics | ||
| + | *Flow diagram to get the VLP curve | ||
| + | *Workflow to find HL | ||
== Flow Diagram == | == Flow Diagram == | ||
| Line 55: | Line 66: | ||
:<math> v_{SL} = \frac{5.615 q_L}{86400 A_p} \left ( B_o \frac{1}{1+WOR} + B_w \frac{WOR}{1+WOR} \right )</math><ref name= Lyons/> | :<math> v_{SL} = \frac{5.615 q_L}{86400 A_p} \left ( B_o \frac{1}{1+WOR} + B_w \frac{WOR}{1+WOR} \right )</math><ref name= Lyons/> | ||
| − | :<math> v_{SG} = \frac{q_L \left ( GLR-R_s \left( \frac{1}{1+WOR}\right) \right )}{86400 A_p}\ \frac{14.7}{p}\ \frac{ | + | :<math> v_{SG} = \frac{q_L \left ( GLR-R_s \left( \frac{1}{1+WOR}\right) \right )}{86400 A_p}\ \frac{14.7}{p}\ \frac{T_R}{520}\ \frac{z}{1}</math><ref name= Lyons/> |
:<math> N_{LV} = 1.938\ v_{SL}\ \sqrt[4]{\frac{\rho_L}{\sigma_L}} </math><ref name= HB/> | :<math> N_{LV} = 1.938\ v_{SL}\ \sqrt[4]{\frac{\rho_L}{\sigma_L}} </math><ref name= HB/> | ||
| Line 94: | Line 105: | ||
:<math> h </math> = depth, ft | :<math> h </math> = depth, ft | ||
:<math> H </math> = correlation group, dimensionless | :<math> H </math> = correlation group, dimensionless | ||
| − | :<math> H_L </math> = liquid holdup factor, | + | :<math> H_L </math> = liquid holdup factor, fraction |
:<math> f </math> = friction factor, dimensionless | :<math> f </math> = friction factor, dimensionless | ||
:<math> GLR </math> = gas-liquid ratio, scf/bbl | :<math> GLR </math> = gas-liquid ratio, scf/bbl | ||
| Line 212: | Line 223: | ||
[[Category:pengtools]] | [[Category:pengtools]] | ||
[[Category:PQplot]] | [[Category:PQplot]] | ||
| + | |||
| + | {{#seo: | ||
| + | |title=Hagedorn and Brown correlation | ||
| + | |titlemode= replace | ||
| + | |keywords=Hagedorn and Brown, correlation, equation, flow rate, fluids flow, Reynolds number, liquid hold up | ||
| + | |description=Hagedorn and Brown correlation used to calculate reservoir inflow performance curve for nodal analysis | ||
| + | }} | ||
Latest revision as of 12:21, 1 November 2018
Contents
Brief
Hagedorn and Brown is an empirical two-phase flow correlation published in 1965 [1].
It doesn't distinguish between the flow regimes.
The heart of the Hagedorn and Brown method is a correlation for the liquid holdup HL [2].
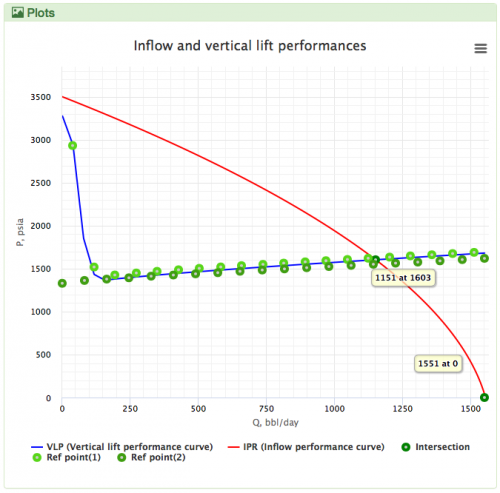
Hagedorn and Brown is the default VLP correlation for the oil wells in the PQplot.
Math & Physics
Following the law of conservation of energy the basic steady state flow equation is:
where
Colebrook–White [3] equation for the Darcy's friction factor:
Reynolds two phase number:
Discussion
Why Hagedorn and Brown?
One of the consistently best correlations ...— Michael Economides et al[2]
Demo
Hagedorn and Brown correlation overview video:
In this video it's shown:
- What the Hagedorn and Brown correlation is
- History and practical application
- Math & Physics
- Flow diagram to get the VLP curve
- Workflow to find HL
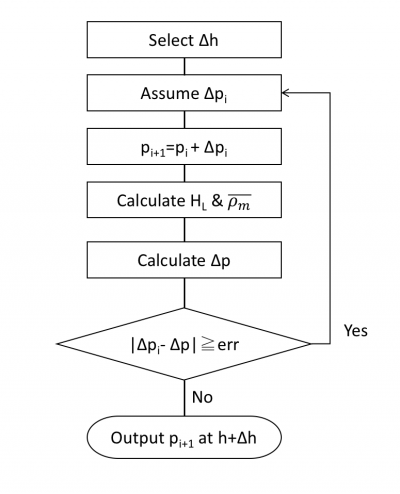
Flow Diagram
Workflow HL
Modifications
1. Use the no-slip holdup when the original empirical correlation predicts a liquid holdup HL less than the no-slip holdup [2].
2. Use the Griffith correlation to define the bubble flow regime[2] and calculate HL.
3. Use watercut instead of WOR to account for the watercut = 100%.
Nomenclature
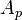 = flow area, ft2
= flow area, ft2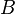 = correlation group, dimensionless
= correlation group, dimensionless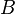 = formation factor, bbl/stb
= formation factor, bbl/stb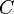 = coefficient for liquid viscosity number, dimensionless
= coefficient for liquid viscosity number, dimensionless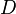 = pipe diameter, ft
= pipe diameter, ft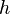 = depth, ft
= depth, ft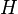 = correlation group, dimensionless
= correlation group, dimensionless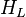 = liquid holdup factor, fraction
= liquid holdup factor, fraction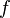 = friction factor, dimensionless
= friction factor, dimensionless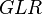 = gas-liquid ratio, scf/bbl
= gas-liquid ratio, scf/bbl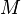 = total mass of oil, water and gas associated with 1 bbl of liquid flowing into and out of the flow string, lbm/bbl
= total mass of oil, water and gas associated with 1 bbl of liquid flowing into and out of the flow string, lbm/bbl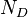 = pipe diameter number, dimensionless
= pipe diameter number, dimensionless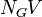 = gas velocity number, dimensionless
= gas velocity number, dimensionless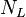 = liquid viscosity number, dimensionless
= liquid viscosity number, dimensionless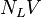 = liquid velocity number, dimensionless
= liquid velocity number, dimensionless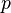 = pressure, psia
= pressure, psia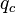 = conversion constant equal to 32.174049, lbmft / lbfsec2
= conversion constant equal to 32.174049, lbmft / lbfsec2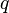 = total liquid production rate, bbl/d
= total liquid production rate, bbl/d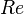 = Reynolds number, dimensionless
= Reynolds number, dimensionless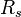 = solution gas-oil ratio, scf/stb
= solution gas-oil ratio, scf/stb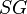 = specific gravity, dimensionless
= specific gravity, dimensionless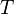 = temperature, °R or °K, follow the subscript
= temperature, °R or °K, follow the subscript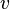 = velocity, ft/sec
= velocity, ft/sec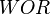 = water-oil ratio, bbl/bbl
= water-oil ratio, bbl/bbl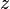 = gas compressibility factor, dimensionless
= gas compressibility factor, dimensionless
Greek symbols
 = absolute roughness, ft
= absolute roughness, ft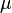 = viscosity, cp
= viscosity, cp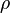 = density, lbm/ft3
= density, lbm/ft3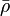 = integrated average density at flowing conditions, lbm/ft3
= integrated average density at flowing conditions, lbm/ft3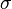 = surface tension of liquid-air interface, dynes/cm (ref. values: 72 - water, 35 - oil)
= surface tension of liquid-air interface, dynes/cm (ref. values: 72 - water, 35 - oil)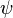 = secondary correlation factor, dimensionless
= secondary correlation factor, dimensionless
Subscripts
- g = gas
- K = °K
- L = liquid
- m = gas/liquid mixture
- o = oil
- R = °R
- SL = superficial liquid
- SG = superficial gas
- w = water
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 Hagedorn, A. R.; Brown, K. E. (1965). "Experimental study of pressure gradients occurring during continuous two-phase flow in small-diameter vertical conduits"
 . Journal of Petroleum Technology. 17(04) (SPE-940-PA): 475–484.
. Journal of Petroleum Technology. 17(04) (SPE-940-PA): 475–484.
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 Economides, M.J.; Hill, A.D.; Economides, C.E.; Zhu, D. (2013). Petroleum Production Systems (2 ed.). Westford, Massachusetts: Prentice Hall. ISBN 978-0-13-703158-0.
- ↑ Colebrook, C. F. (1938–1939). "Turbulent Flow in Pipes, With Particular Reference to the Transition Region Between the Smooth and Rough Pipe Laws"
 . Journal of the Institution of Civil Engineers. London, England. 11: 133–156.
. Journal of the Institution of Civil Engineers. London, England. 11: 133–156.
- ↑ Moody, L. F. (1944). "Friction factors for pipe flow"
 . Transactions of the ASME. 66 (8): 671–684.
. Transactions of the ASME. 66 (8): 671–684.
- ↑ 5.0 5.1 5.2 5.3 5.4 5.5 Lyons, W.C. (1996). Standard handbook of petroleum and natural gas engineering. 2. Houston, TX: Gulf Professional Publishing. ISBN 0-88415-643-5.
- ↑ 6.0 6.1 Trina, S. (2010). An integrated horizontal and vertical flow simulation with application to wax precipitation (Master of Engineering Thesis). Canada: Memorial University of Newfoundland.
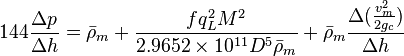
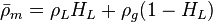
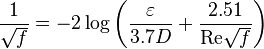
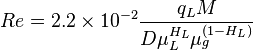

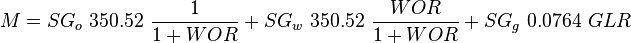
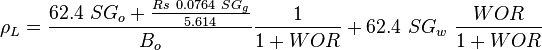
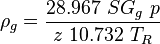
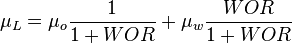
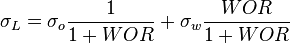
![N_L = 0.15726\ \mu_L \sqrt[4]{\frac{1}{\rho_L \sigma_L^3}}](/images/math/b/2/0/b207fe79b4a4ee53d466e182791ca737.png)
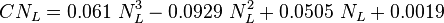
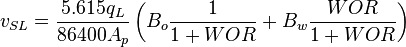
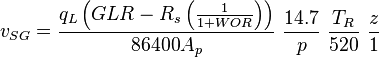
![N_{LV} = 1.938\ v_{SL}\ \sqrt[4]{\frac{\rho_L}{\sigma_L}}](/images/math/d/d/8/dd824df0b6ec22aa724161b929e993fe.png)
![N_{GV} = 1.938\ v_{SG}\ \sqrt[4]{\frac{\rho_L}{\sigma_L}}](/images/math/3/6/4/364153c39c1657b3b7bab8f7ed710e60.png)