Difference between revisions of "Category: FracDesign"

From wiki.pengtools.com
Jump to: navigation, search
(→‎Carter opening time distribution factor KL)
(→‎Carter opening time distribution factor KL)
Line 62: Line 62:
 
====Carter opening time distribution factor K<sub>L</sub>====
 
====Carter opening time distribution factor K<sub>L</sub>====
  
−
:<math>K_L=-\frac{S_p}{C_L \sqrt{t_e}} - \frac{w_{f,hydr,avg}}{2C_L\sqrt{t_e}} + \frac{w_{f,hydr,avg}}{2 \eta_e C_L \sqrt{t_e}}</math> (ref <ref name = UFD2002/> eq 4.8)
+
:<math>K_L=-\frac{S_p}{C_L \sqrt{t_e}} - \frac{w_{f,hydr,avg}}{2C_L\sqrt{t_e}} + \frac{w_{f,hydr,avg}}{2 \eta C_L \sqrt{t_e}}</math> (ref <ref name = UFD2002/> eq 4.8)
  
 
where:
 
where:
  
−
:<math>\eta_e=\frac{w_{f,hydr,avg}(w_{f,hydr,avg}+2S_p)}{4\pi {C_L}^2 t_e} \left ( exp(\beta^2) erfc(\beta) + \frac{2\beta}{\sqrt\pi} - 1 \right )</math>(ref <ref name = UFD2002/> table 7-5, p.111)
+
:<math>\eta=\frac{w_{f,hydr,avg}(w_{f,hydr,avg}+2S_p)}{4\pi {C_L}^2 t_e} \left ( exp(\beta^2) erfc(\beta) + \frac{2\beta}{\sqrt\pi} - 1 \right )</math>(ref <ref name = UFD2002/> table 7-5, p.111)
  
 
and:
 
and:

Revision as of 08:54, 9 October 2018

Brief

pengtools fracDesign

fracDesign is a tool for designing a hydraulic fracture treatment in pengtools.

For the given set of reservoir, fluid and proppant properties fracDesign calculates the pumping schedule which will create the optimal fracture geometry to achieve maximum well’s productivity.

fracDesignis available online at www.pengtools.com.

Main features

  • PKN and KGD fracture geometry models
  • optiFrac workflow on fracture geometry optimization
  • Slurry concentration versus time pumping schedule as plot and table
  • Fracture length and width profiles vs time plots
  • Net pressure profiles vs time as plot and table
  • Practical pumping constrains and Fracture tuning options
  • Detailed output table with calculated fracture design parameters
  • Sensitivity option with benchmark to potential
  • Simulation mode: calculating the fracture geometry from the given pumping schedule

Interface features

  • "Default values" button resets input values to the default values.
  • Switch between Metric and Field units.
  • Save/load models to the files and to the user’s cloud.
  • Export pdf report containing input parameters, calculated values and the chart.
  • Share models to the public cloud or by using model’s link.
  • Continue your work from where you stopped: last saved model will be automatically opened.
  • Download the chart as an image or data and print (upper-right corner chart’s button).

Math & Physics

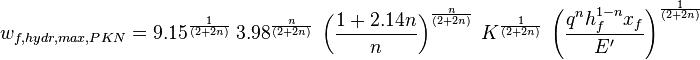w_{f,hydr,max,PKN}=9.15^{\frac{1}{(2 + 2 n)}}\ 3.98^{\frac{n}{(2 + 2 n)}}\ \left ( \frac{1+2.14n}{n}\right )^{\frac{n}{(2 + 2 n)}}\ K^{\frac{1}{(2 + 2 n)}}\ \left ( \frac{q^n h_f^{1-n} x_f}{E'} \right )^{\frac{1}{(2 + 2 n)}} - hydraulic maximum fracture width PKN (ref[1] eq 9.53)
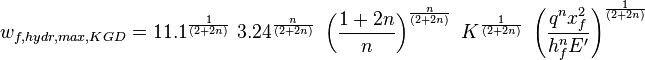w_{f,hydr,max,KGD}=11.1^{\frac{1}{(2 + 2 n)}}\ 3.24^{\frac{n}{(2 + 2 n)}}\ \left ( \frac{1+2n}{n}\right )^{\frac{n}{(2 + 2 n)}}\ K^{\frac{1}{(2 + 2 n)}}\ \left ( \frac{q^n x_f^2}{h_f^n E'} \right )^{\frac{1}{(2 + 2 n)}} - hydraulic maximum fracture width KGD (ref[1] eq 9.55)
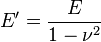E'=\frac{E}{1-\nu^2} - plain strain modulus
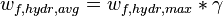w_{f,hydr,avg} = w_{f,hydr,max} * \gamma - hydraulic average fracture width
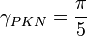\gamma_{PKN}=\frac{\pi}{5} - shape factor PKN (ref[1] eq 9.10)
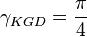\gamma_{KGD}=\frac{\pi}{4} - shape factor KGD (ref[1] eq 9.24)
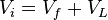V_i = V_f + V_L - mass balance equation (ref[1] eq 8.1)
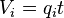V_i = q_i t - injected volume into one fracture wing
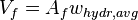V_f = A_f w_{hydr,avg} - volume of fluid contained in one fracture wing
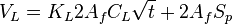V_L = K_L 2 A_f C_L \sqrt{t} + 2 A_f S_p - volume of fluid leak-off to formation through the two created fracture surfaces of one wing
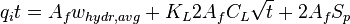q_i t = A_f w_{hydr,avg} + K_L 2 A_f C_L \sqrt{t} + 2 A_f S_p - mass balance equation (ref[2] eq 4.6)
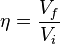\eta = \frac{V_f}{V_i} - fluid efficiency

Nolte opening time distribution factor KL

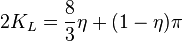2 K_L=\frac{8}{3} \eta + ( 1 - \eta) \pi - (ref[1] eq 8.36)

Carter opening time distribution factor KL

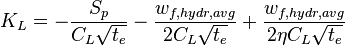K_L=-\frac{S_p}{C_L \sqrt{t_e}} - \frac{w_{f,hydr,avg}}{2C_L\sqrt{t_e}} + \frac{w_{f,hydr,avg}}{2 \eta C_L \sqrt{t_e}} (ref [2] eq 4.8)

where:

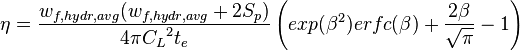\eta=\frac{w_{f,hydr,avg}(w_{f,hydr,avg}+2S_p)}{4\pi {C_L}^2 t_e} \left ( exp(\beta^2) erfc(\beta) + \frac{2\beta}{\sqrt\pi} - 1 \right )(ref [2] table 7-5, p.111)

and:

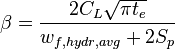\beta=\frac{2C_L \sqrt{\pi t_e}}{w_{f,hydr,avg} + 2S_p}(ref [2] table 7-5, p.111)

G-function for opening time distribution factor KL

References

  1. ↑ 1.0 1.1 1.2 1.3 1.4 1.5 Valko, Peter; Economides, Michael J. (1995). Hydraulic fracture mechanics. Texas A & M University: John Wiley and Sons. 
  2. ↑ 2.0 2.1 2.2 2.3 Economides, Michael J.; Oligney, Ronald; Valko, Peter (2002). Unified Fracture Design: Bridging the Gap Between Theory and Practice. Alvin, Texas: Orsa Press. 
Retrieved from "https://wiki.pengtools.com/index.php?title=Category:FracDesign&oldid=4913"