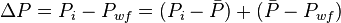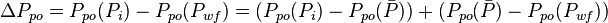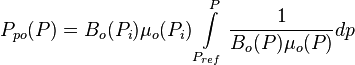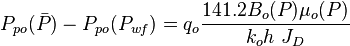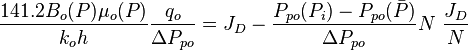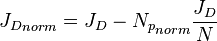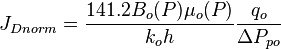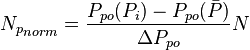Difference between revisions of "Oil Flowing Material Balance"
(→Case Study) |
|||
| Line 76: | Line 76: | ||
All the input data is attached to the Case Study for the reference. | All the input data is attached to the Case Study for the reference. | ||
| − | Download the Case Study: [[File:oilFMB_CaseStudy.pdf| Download Case Study (pdf)]] | + | Download the Case Study: [[File:oilFMB_CaseStudy.pdf|Download Case Study (pdf)]] |
Download the input well production data: [[File:well 8 daily data.csv]] | Download the input well production data: [[File:well 8 daily data.csv]] | ||
Revision as of 08:17, 19 April 2018
Contents
Brief
Oil Flowing Material Balance (Oil FMB) is the advanced engineering technique published in 2005 by Louis Mattar and David Anderson [1].
Oil Flowing Material Balance is applied to determine:
- Reservoirs STOIIP & EUR
- Well's EUR and JD
Oil Flowing Material Balance uses readily available Well flowing data: production rate and bottomhole pressure.
The interpretation technique is fitting the data points with the straight lines to estimate STOIIP and JD.
Math & Physics
The total pressure drop at the wellbore is:
Where
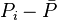 , is pressure drop due to depletion defined by the Oil Material Balance
, is pressure drop due to depletion defined by the Oil Material Balance
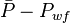 , is pressure drop due to Darcy's law
, is pressure drop due to Darcy's law
In terms of oil pseudo pressure the total pressure drop is:
Where
Finally, the Oil Flowing Material Balance equation:
Or
Where
Discussion
Oil Flowing Material Balance can be applied to:
- single well
- multiple wells producing from the same Reservoir.
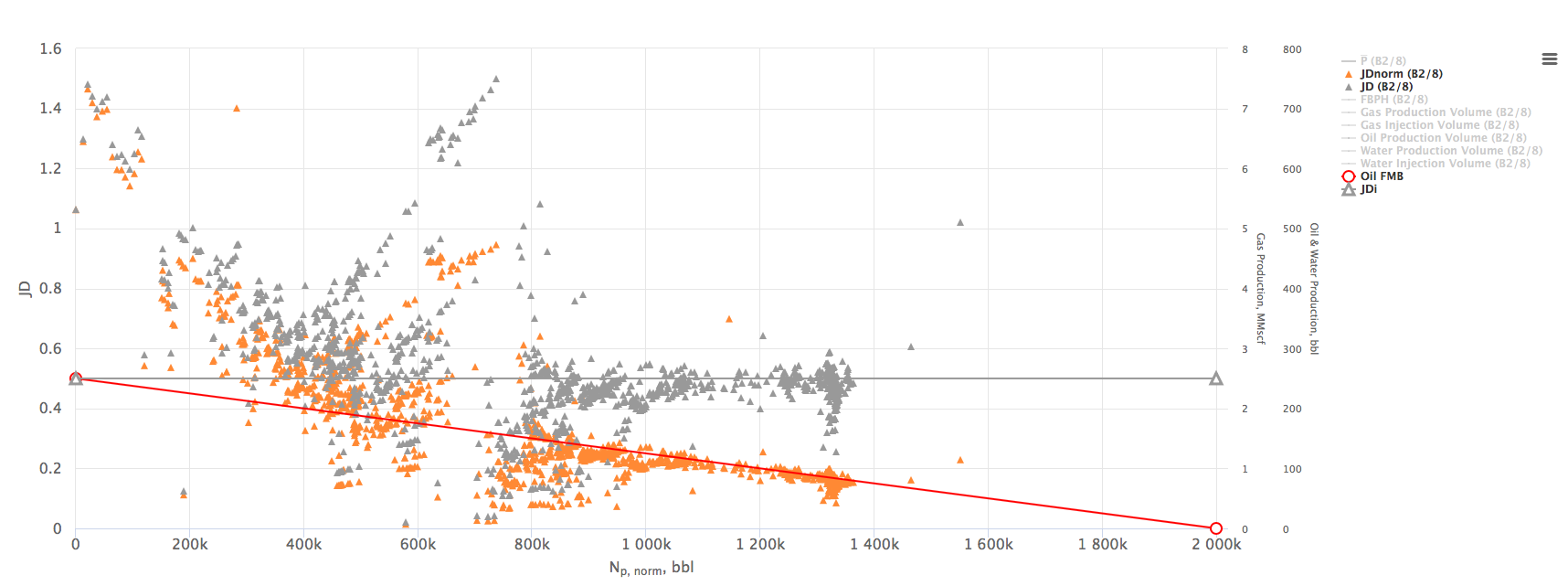
The X axis on the Oil Flowing Material Balance Plot can be selected as:
Note what Oil Flowing Material Balance accounts for the changing PVT properties of the oil with pressure.
Case Study
This Case Study demonstrates the application of the Oil Flowing Material Balance engineering technique using the E&P Portal.
The Study is based on the oil well from a field in West Siberia, Russia.
It is shown how to:
- Input the data to the E&P Portal;
- Apply the Oil FMB to estimate the well's STOIIP and JD;
- Save and export the analysis results.
All the input data is attached to the Case Study for the reference.
Download the Case Study: File:OilFMB CaseStudy.pdf
Download the input well production data: File:Well 8 daily data.csv
Workflow
- Upload the data required
- Open the Oil Flowing Material Balance tool here
- Estimate the N (red line X-axis intercept)
- Calculate the average reservoir pressure
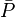 based on N, known production data and using Oil Material Balance equation
based on N, known production data and using Oil Material Balance equation - Calculate the
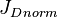
- Calculate the
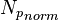
- Plot the orange
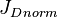 vs
vs 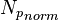 line:
line: - Change the N to match the orange line with the red one
- Change the gray JD line Y-axis intercept to match the changing JD
- Save the Oil Flowing Material Balance model
- Move to the next well
Data required
- Create Field here
- Create or Upload Reservoirs here
- Input the Reservoirs GIIP and STOIIP here
- Create or Upload PVT (SG, Pi, Ti) here
- Upload Wells
- Create or Upload Wells Perforations here
- Create or Upload kh and JD here
- Upload Daily Measures
In case you need to calculate the flowing bottomhole pressure from the wellhead pressure:
- Calculate the flowing bottomhole pressures using BHP Calculator
- Export flowing bottomhole pressures to Daily Measures here
In case you want to add the static reservoir pressures on the FMB Plot:
- Create or Upload the static reservoir pressures, here
- Calculate Monthly Measures from the Daily Measures using Monthly Data Calculator
Nomenclature
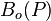 = oil formation volume factor as a function of pressure, bbl/stb
= oil formation volume factor as a function of pressure, bbl/stb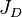 = dimensionless productivity index, dimensionless
= dimensionless productivity index, dimensionless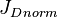 = dimensionless productivity index in terms of the oil pseudo pressure, dimensionless
= dimensionless productivity index in terms of the oil pseudo pressure, dimensionless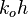 = oil permeability times thickness, md*ft
= oil permeability times thickness, md*ft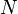 = stock tank oil initially in place, stb
= stock tank oil initially in place, stb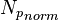 = normalized cumulative oil production, stb
= normalized cumulative oil production, stb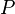 = pressure, psia
= pressure, psia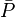 = average reservoir pressure, psia
= average reservoir pressure, psia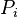 = initial pressure, psia
= initial pressure, psia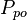 = oil pseudo pressure, psia
= oil pseudo pressure, psia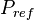 = reference pressure, psia
= reference pressure, psia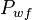 = well flowing pressure, psia
= well flowing pressure, psia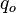 = oil rate, stb
= oil rate, stb
Greek symbols
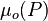 = oil viscosity as a function of pressure, cp
= oil viscosity as a function of pressure, cp
References
- ↑ 1.0 1.1 Mattar, L.; Anderson, D (2005). "Dynamic Material Balance (Oil or Gas-In-Place Without Shut-Ins)" (PDF). CIPC.
- ↑ 2.0 2.1 Stalgorova, Louis; Mattar, Ekaterina (2016). "Analytical Methods for Single-Phase Oil Flow: Accounting for Changing Liquid and Rock Properties". Society of Petroleum Engineers.