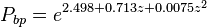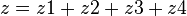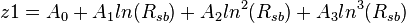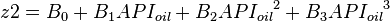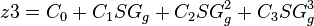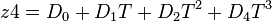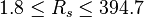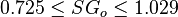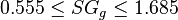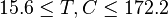Difference between revisions of "Valko - McCain bubble point pressure correlation"
From wiki.pengtools.com
(→Example. Calculation of the bubble point pressure) |
|||
| Line 5: | Line 5: | ||
[[Valko - McCain bubble point pressure correlation|Valko - McCain]] is an empirical correlation for the '''bubble point''' pressure published in '''2003''' <ref name={Valko - McCain}/>. | [[Valko - McCain bubble point pressure correlation|Valko - McCain]] is an empirical correlation for the '''bubble point''' pressure published in '''2003''' <ref name={Valko - McCain}/>. | ||
| − | [[File:Valko McCain Bubble Point Pressure.png|thumb|right|400px|link=https://www.pengtools.com/pvtCalculator?paramsToken=de71e4cc29541ab2117e07408864410c|Valko McCain Bubble Point Pressure in PVT Software]] | + | [[File:Valko McCain Bubble Point Pressure.png|thumb|right|400px|link=https://www.pengtools.com/pvtCalculator?paramsToken=de71e4cc29541ab2117e07408864410c|Valko McCain Bubble Point Pressure correlation in the PVT Software]] |
== Math & Physics == | == Math & Physics == | ||
Latest revision as of 08:50, 28 September 2020
Contents
Valko - McCain bubble point pressure correlation
Valko - McCain is an empirical correlation for the bubble point pressure published in 2003 [1].
Math & Physics
where:
A0 = -4.814074834
A1 = 0.7480913
A2 = 0.1743556
A3 = -0.0206
B0 = 1.27
B1 = -0.0449
B2 = 4.36e-4
B3 = -4.76e-6
C0 = 4.51
C1 = -10.84
C2 = 8.39
C3 = -2.34
D0 = -7.2254661
D1 = 0.043155
D2 = -8.55e-5
D3 = 6.00696e-8
Application range
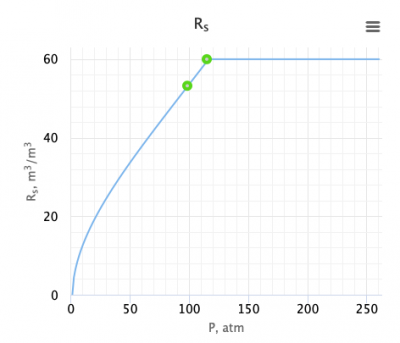
Example. Calculation of the bubble point pressure
Example source [3]
Input data
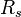 = 60 sm3/sm3
= 60 sm3/sm3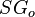 = 0.85 or 35 API
= 0.85 or 35 API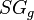 = 0.75
= 0.75 = 90C or 363K
= 90C or 363K
Calculate bubble point pressure?
Solution
z1=-0.2422
z2=0.0294
z3=0.1122
z4=-0.0594
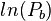 = 2.4557
= 2.4557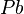 = 11.65MPa or 115 atm
= 11.65MPa or 115 atm
The solution is available in the online PVT calculator software at www.pengtools.com
Nomenclature
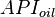 = oil specific gravity, °API
= oil specific gravity, °API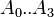 = coefficients
= coefficients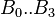 = coefficients
= coefficients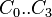 = coefficients
= coefficients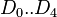 = coefficients
= coefficients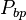 = bubble point pressure, MPa
= bubble point pressure, MPa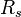 = solution oil gas ratio, sm3/sm3
= solution oil gas ratio, sm3/sm3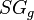 = gas specific gravity, dimensionless
= gas specific gravity, dimensionless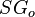 = oil specific gravity, dimensionless
= oil specific gravity, dimensionless = temperature, °K
= temperature, °K
References
- ↑
Valkó, P. P.; McCain, W.D. (2003). "Reservoir oil bubblepoint pressures revisited; solution gas–oil ratios and surface gas specific gravities."
 . J. Pet. Sci. Eng. 37 (3–4): 153-169.
. J. Pet. Sci. Eng. 37 (3–4): 153-169.
- ↑ Afanasyev, Vitaliy; Moskvin, Igor; Wolcott, Ken; McCain, W.D. (2004). "Practical PVT Calculations for black oils". YUKOS publication.
- ↑
Wolcott, Don (2009). Applied Waterflood Field Development
 . Houston: Energy Tribune Publishing Inc.
. Houston: Energy Tribune Publishing Inc.